Kalman Filter - Introduction
Kalman filter is probably the most popular filtering algorithm used in many areas of science and technology. Due to its simplicity and efficiency, it can be found in GPS receivers, handlers of sensor readings, in the implementation of control systems, etc.
There are a lot of articles and books about the Kalman filter on the Internet (mostly in English), but these articles have a rather large threshold of entry, there are a lot of vague places, although in fact it is a very clear and transparent algorithm. I will try to talk about it in simple language, with a gradual increase in complexity.
Any measuring device has a certain error, it can be influenced by a large number of external and internal influences, which leads to the fact that the information from it is noisy. The more noisy the data, the more difficult it is to process such information.
A filter is a data processing algorithm that removes noise and unnecessary information. In the Kalman filter, it is possible to set a priori information about the nature of the system, the relationship of variables, and on the basis of this to build a more accurate estimate, but even in the simplest case (without entering a priori information), it gives excellent results.
')
Consider the simplest example - suppose we need to control the level of fuel in the tank. To do this, a capacitive sensor is installed in the tank, it is very easy to maintain, but it has some drawbacks - for example, dependence on fuel to be filled (the dielectric constant of the fuel depends on many factors, for example, on temperature), a large influence of the “bump” in the tank. As a result, the information from it represents a typical “saw” with a decent amplitude. These types of sensors are often installed on heavy mining equipment (do not be embarrassed by the volume of the tank):
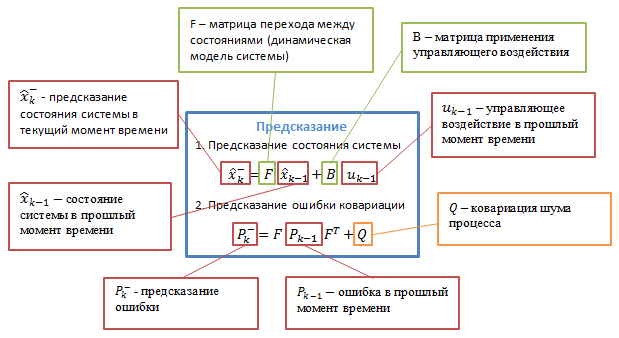
Let's digress a bit and get acquainted with the algorithm itself. The Kalman filter uses a dynamic model of the system (for example, the physical law of motion), known control actions, and a number of consecutive measurements to form an optimal state estimate. The algorithm consists of two repeating phases: prediction and adjustment. The first one calculates the prediction of the state at the next time point (taking into account the inaccuracy of their measurement). On the second, the new information from the sensor corrects the predicted value (also taking into account the inaccuracy and noise of this information):

The equations are presented in the matrix form, if you do not know linear algebra - no problem, then there will be a simplified version without matrices for the case with one variable. In the case of a single variable, the matrices degenerate into scalar values.
We first understand the notation: the subscript denotes the moment in time: k is the current, (k-1) is the previous one, the minus sign in the superscript indicates that it is a predicted intermediate value.
Variable descriptions are presented in the following images:
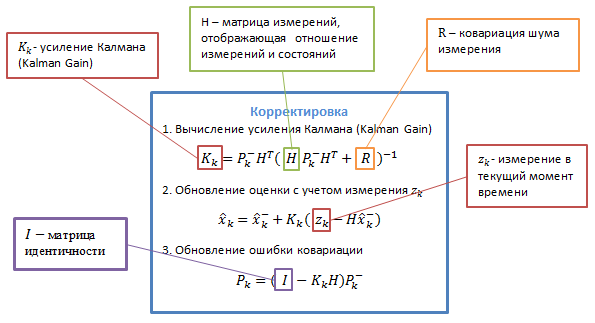
It can be long and tedious to describe what all these mysterious transition matrices mean, but in my opinion, it’s better to try using an algorithm using a real example - so that the abstract values have a real meaning.
Let us return to the example with the fuel level sensor, since the state of the system is represented by one variable (the volume of fuel in the tank), then the matrices degenerate into ordinary equations:
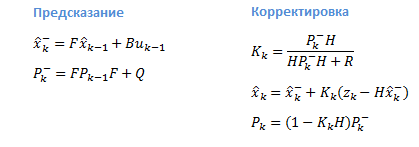
In order to apply a filter, it is necessary to determine the matrices / values of variables defining the dynamics of the system and the measurements of F, B and H:
F is a variable describing the dynamics of the system; in the case of fuel, this can be a factor determining the fuel consumption at idle speed during the sampling time (the time between the steps of the algorithm). However, in addition to fuel consumption, there are also refueling ... so for simplicity we take this variable equal to 1 (that is, we indicate that the predicted value will be equal to the previous state).
B - variable defining the use of control action. If we had additional information about the engine speed or the degree of accelerator pedal depression, this parameter would determine how the fuel consumption changes during the sampling time. Since there are no control actions in our model (there is no information about them), we take B = 0.
H is the matrix defining the relationship between measurements and the state of the system, while without explanation we take this variable also equal to 1.
R - measurement error can be determined by testing measuring instruments and determining the error of their measurement.
Q - determining the noise of a process is a more difficult task, since it is necessary to determine the variance of the process, which is not always possible. In any case, you can choose this parameter to ensure the required level of filtering.
To dispel the remaining obscurities, we implement a simplified algorithm in C # (without matrices and control actions):
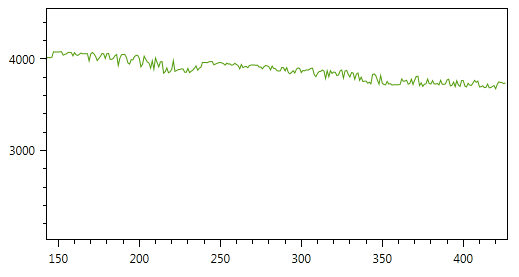
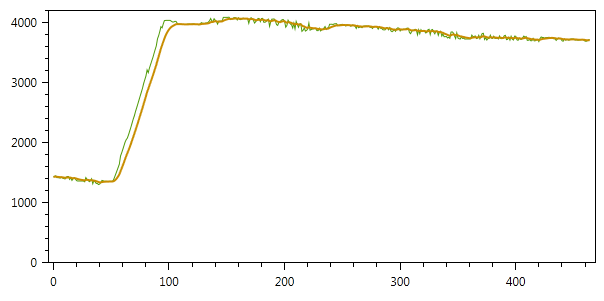
The result of filtering with these parameters is shown in the figure (to adjust the degree of smoothing, you can change the parameters Q and R):
The most interesting thing left behind the article is to apply the Kalman filter for several variables, specify the relationship between them, and automatically display values for unobservable variables. I will try to continue the topic as soon as time appears.
I hope the description turned out not very tedious and difficult, if you still have questions and clarifications - welcome to the comments)
UPD: List of sources:
CS373 - PROGRAMMING A ROBOTIC CAR - highly recommended
Wikipedia (Russian)
Wikipedia (English)
On Habré: 1 and 2
More serious sources are:
Greg Welch, Gary Bishop, An Introduction to the Kalman Filter, 2001
MSGrewal, AP Andrews, Kalman Filtering - Theory and Practice Using MATLAB, Wiley, 2001
UPD2: the example given in the article is purely demonstrative. The main application of the filter is more complex systems. For example, in the case of determining the coordinates of the car, you can associate gps-coordinates, steering angle, engine speed ... and all this will give an increase in the accuracy of coordinates.
There are a lot of articles and books about the Kalman filter on the Internet (mostly in English), but these articles have a rather large threshold of entry, there are a lot of vague places, although in fact it is a very clear and transparent algorithm. I will try to talk about it in simple language, with a gradual increase in complexity.
What is it for?
Any measuring device has a certain error, it can be influenced by a large number of external and internal influences, which leads to the fact that the information from it is noisy. The more noisy the data, the more difficult it is to process such information.
A filter is a data processing algorithm that removes noise and unnecessary information. In the Kalman filter, it is possible to set a priori information about the nature of the system, the relationship of variables, and on the basis of this to build a more accurate estimate, but even in the simplest case (without entering a priori information), it gives excellent results.
')
Consider the simplest example - suppose we need to control the level of fuel in the tank. To do this, a capacitive sensor is installed in the tank, it is very easy to maintain, but it has some drawbacks - for example, dependence on fuel to be filled (the dielectric constant of the fuel depends on many factors, for example, on temperature), a large influence of the “bump” in the tank. As a result, the information from it represents a typical “saw” with a decent amplitude. These types of sensors are often installed on heavy mining equipment (do not be embarrassed by the volume of the tank):

Kalman filter
Let's digress a bit and get acquainted with the algorithm itself. The Kalman filter uses a dynamic model of the system (for example, the physical law of motion), known control actions, and a number of consecutive measurements to form an optimal state estimate. The algorithm consists of two repeating phases: prediction and adjustment. The first one calculates the prediction of the state at the next time point (taking into account the inaccuracy of their measurement). On the second, the new information from the sensor corrects the predicted value (also taking into account the inaccuracy and noise of this information):

The equations are presented in the matrix form, if you do not know linear algebra - no problem, then there will be a simplified version without matrices for the case with one variable. In the case of a single variable, the matrices degenerate into scalar values.
We first understand the notation: the subscript denotes the moment in time: k is the current, (k-1) is the previous one, the minus sign in the superscript indicates that it is a predicted intermediate value.
Variable descriptions are presented in the following images:


It can be long and tedious to describe what all these mysterious transition matrices mean, but in my opinion, it’s better to try using an algorithm using a real example - so that the abstract values have a real meaning.
Let's test in
Let us return to the example with the fuel level sensor, since the state of the system is represented by one variable (the volume of fuel in the tank), then the matrices degenerate into ordinary equations:
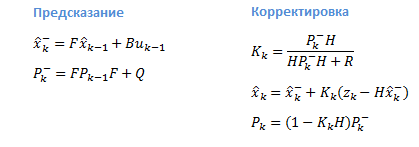
Process Model Definition
In order to apply a filter, it is necessary to determine the matrices / values of variables defining the dynamics of the system and the measurements of F, B and H:
F is a variable describing the dynamics of the system; in the case of fuel, this can be a factor determining the fuel consumption at idle speed during the sampling time (the time between the steps of the algorithm). However, in addition to fuel consumption, there are also refueling ... so for simplicity we take this variable equal to 1 (that is, we indicate that the predicted value will be equal to the previous state).
B - variable defining the use of control action. If we had additional information about the engine speed or the degree of accelerator pedal depression, this parameter would determine how the fuel consumption changes during the sampling time. Since there are no control actions in our model (there is no information about them), we take B = 0.
H is the matrix defining the relationship between measurements and the state of the system, while without explanation we take this variable also equal to 1.
Determination of smoothing properties
R - measurement error can be determined by testing measuring instruments and determining the error of their measurement.
Q - determining the noise of a process is a more difficult task, since it is necessary to determine the variance of the process, which is not always possible. In any case, you can choose this parameter to ensure the required level of filtering.
Implement in code
To dispel the remaining obscurities, we implement a simplified algorithm in C # (without matrices and control actions):
class KalmanFilterSimple1D { public double X0 {get; private set;} // predicted state public double P0 { get; private set; } // predicted covariance public double F { get; private set; } // factor of real value to previous real value public double Q { get; private set; } // measurement noise public double H { get; private set; } // factor of measured value to real value public double R { get; private set; } // environment noise public double State { get; private set; } public double Covariance { get; private set; } public KalmanFilterSimple1D(double q, double r, double f = 1, double h = 1) { Q = q; R = r; F = f; H = h; } public void SetState(double state, double covariance) { State = state; Covariance = covariance; } public void Correct(double data) { //time update - prediction X0 = F*State; P0 = F*Covariance*F + Q; //measurement update - correction var K = H*P0/(H*P0*H + R); State = X0 + K*(data - H*X0); Covariance = (1 - K*H)*P0; } } // ... var fuelData = GetData(); var filtered = new List<double>(); var kalman = new KalmanFilterSimple1D(f: 1, h: 1, q: 2, r: 15); // F, H, Q R kalman.SetState(fuelData[0], 0.1); // State Covariance foreach(var d in fuelData) { kalman.Correct(d); // filtered.Add(kalman.State); // } The result of filtering with these parameters is shown in the figure (to adjust the degree of smoothing, you can change the parameters Q and R):

The most interesting thing left behind the article is to apply the Kalman filter for several variables, specify the relationship between them, and automatically display values for unobservable variables. I will try to continue the topic as soon as time appears.
I hope the description turned out not very tedious and difficult, if you still have questions and clarifications - welcome to the comments)
UPD: List of sources:
CS373 - PROGRAMMING A ROBOTIC CAR - highly recommended
Wikipedia (Russian)
Wikipedia (English)
On Habré: 1 and 2
More serious sources are:
Greg Welch, Gary Bishop, An Introduction to the Kalman Filter, 2001
MSGrewal, AP Andrews, Kalman Filtering - Theory and Practice Using MATLAB, Wiley, 2001
UPD2: the example given in the article is purely demonstrative. The main application of the filter is more complex systems. For example, in the case of determining the coordinates of the car, you can associate gps-coordinates, steering angle, engine speed ... and all this will give an increase in the accuracy of coordinates.
Source: https://habr.com/ru/post/140274/
All Articles