Part number 4. Biochemistry on folding. How to evaluate the course of folding of single-stranded RNA?
So, if you are not tired of the “Hello, RNA World” cycle, catch the latest article of the season :)
In the last article I explained why it should (or at least it is advisable) to abandon the assessment of energy as a target function. If someone does not know, the objective function is such a function invented by us according to which we can estimate whether we are approaching the goal we have set or not, i.e. “Right” fold RNA or not.
If energy is a poorly representative goal, then what is more stable / clearer about where to go? If we had an absolutely formalized and precise goal, this would already mean that we had solved the problem, since the very formalization of the objective function is nothing more than a complete understanding of the process.
')
But we have no such luxury. We are forced to first put forward a hypothesis - which laws the process obeys, and reflect this in the objective function in a certain way.
Once again about energy as a target function - in Rosseta @ home for RNA, it was such
SCORE = (VDW * 3.0 + RG) + (RNA_BS + RNA_BP_W + RNA_BP_H + RNA_BP_S) + (RNA_NONB * 1.5 + RNA_O2ST + RNA_PHOS) + (RNA_AXIS * 0.2 + RNA_STAG * 0.5)
I will not decipher. But it is important that this is a certain sum of the contributions of the various supposed actions. The result is something arithmetic mean. And accordingly, we are moving towards something amorphous. No one will give exact coefficients at the parameters, what contribution a particular parameter makes. And it is impossible to calculate them - after all, we are building a target function. Guessing is also not the case. At first I tried - and found out that more than half simply does not make a serious contribution, but only rejects the calculations not where it is needed.
Therefore, I left at the beginning only VDW - this is a kind of generalized coefficient, in fact it shows whether there are forbidden covalent bonds (as discussed in the first articles). And over time, I replaced it with just the yes / no answer, because it happened that other parameters - sometimes they were outweighed - and as a result intersections were obtained in the .pdb file, which should not be.
Further, we remember that I proposed to base only on the formation of hydrogen bonds. When they are formed we know mathematically without any far-fetched things: distance and angle are everything. Where in the RNA they are - we also consistently know. (more precisely, it is now quite well predicted, there are nuances - but then).
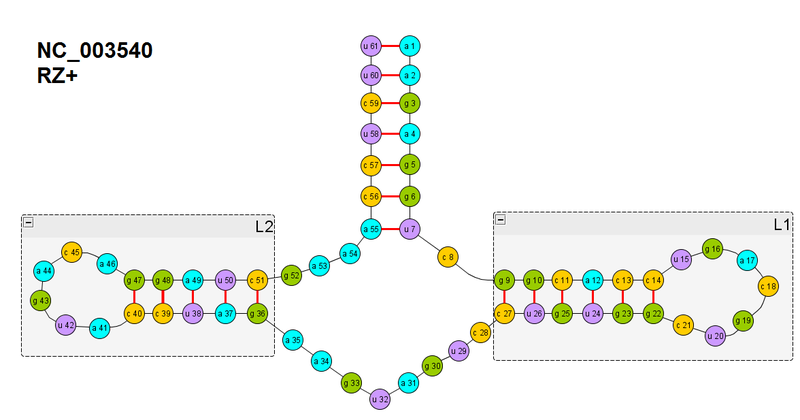
In the figure, the secondary structure of a single ribozyme, which I took for experiments
To simplify my life, I began with the already existing hypothesis that RNA / proteins fold up hierarchically: the so-called Hierarchical model, which has a number of variations, but the essence is this: first, begin to form elements of the secondary structure in the expanded chain. If we focus on the word “begin”, then this is a completely normal hypothesis, but sometimes it is understood in such a way that secondary structures are fully formed, and only then does further folding occur. This is somewhat incorrect. But it will be important for us later, when we completely turn off the ribozyme (I’ll say right away, I haven’t finally succeeded in it - according to my criteria, but they turned out to be tougher, because I do not base on energy, where it’s not clear that the minimum is reached or can be even better But I seem to be close to the decision.).
And now let's turn at least a small area, form hydrogen bonds between the two nucleotides. Take the right loop cugacgucg (from 14 to 22) - 9 nucleotides and form a hydrogen bond between the extreme cg.
How to build a target function?
Three hydrogen bonds are formed between cg, so we have three distances (r1, r2, r3) and three angles (a1, a2, a3). In order for the function to be speaking, we need to be like this: if its value is finally zero and less, then all 3 hydrogen bonds are formed. A positive value should smoothly show an approximation to this state.
Therefore, it is necessary to subtract 3 agstroms from current distances, and 20 degrees from angles. We obtain the values that make a positive contribution to the function. I would like to spit all these 3 corners and 3 distances - and get the value of the objective function. But the distances and angles are not serious, different values. Therefore, there is such a method of reduction to the same scale. Significant distances (after subtracting 3) are somewhere between 1 and 12. Significant in the sense that the angle already affects these distances. And if the distance is greater, then the angle is not important: what difference does it make if atoms are turned, if a chasm separates them. And we have angles from 0 to 180, minus 20 = 160.
If you estimate roughly it turns out that if you multiply the distance by 10, then the distances and angles will be on the same scale. Therefore, we do:
r1 - = 3.0f; r1 * = 10;
r2 - = 3.0f; r2 * = 10;
r3 - = 3.0f; r3 * = 10;
a1 - = 20;
a2 - = 20;
a3 - = 20;
Next, there are two options. One
locScore = (r1 + r2 + r3 + a1 + a2 + a3)
and second
if (maxR> maxA)
{locScore = maxR; }
else
{locScore = maxA; }
where maxR = maximum from (r1, r2, r3), and maxA = maximum from (a1, a2, a3)
Each of the options is good in its own way. To start folding good second. After having already a rough structure, the first one can come in handy.
Well, the algorithm is very simple: we begin to rotate (in part 3 - we remember that we have selected 1500 possible turns) nucleotides with numbers
14
15
sixteen
17
18 - for example, it is here that the turn with number 210 is the best among all
nineteen
20
21
22
rotate say two angles №1 and №6 (i.e. №16). Finding the best fix. Our little chain will fold in two. After some time, we pound the “tension” in such a way (the left and right ends tend to connect, and the loop is under stress) our chain, that in corners 1 and 6 it stops rotating, and the algorithm loops. As soon as it ceases to give the best state, we change the combination of angles, for example, 3 and 4 (No. 34), etc. This will gradually relieve the voltage in corners 1 and 6, and then you can try to “compress” it.
This algorithm is quite enough for the required hydrogen bond to form.
In the next article of the second season :) let's talk about what difficulties appear in the formation of the entire spiral. But still one spiral.
PS I am very glad that serious comments appeared on the third article. But at the same time it looks like a philistine, a potential FoldIt player or simply supporting bio. distributed computing loses interest. I told some completed part (Hello, RNA World). Further it will not be more difficult, but perhaps the details of the rest are not so interested in the inhabitants (write, if this is not so). I do not deny that I am looking for like-minded people and those with whom you can test hypotheses, but at the same time I am not ready for mass, and the software is also not ready. In general, to whom it is not indifferent to write, then I will soon ripen for the season number two.
An important question for mathematicians :
Above, I described two objective functions.
1. locScore = (r1 + r2 + r3 + a1 + a2 + a3)
2. if (maxR> maxA) {locScore = maxR; } else {locScore = maxA; }
Do you know how to combine them into one? Those. let's say if the first objective function was used 5 times, then the second one was used 5 times and a certain result was obtained (lowering the “energy”). It is necessary that the function obtained after the merge, after its application 5 times, would give the same result as if to apply the first and second in turn. Is it possible?
In the last article I explained why it should (or at least it is advisable) to abandon the assessment of energy as a target function. If someone does not know, the objective function is such a function invented by us according to which we can estimate whether we are approaching the goal we have set or not, i.e. “Right” fold RNA or not.
If energy is a poorly representative goal, then what is more stable / clearer about where to go? If we had an absolutely formalized and precise goal, this would already mean that we had solved the problem, since the very formalization of the objective function is nothing more than a complete understanding of the process.
')
But we have no such luxury. We are forced to first put forward a hypothesis - which laws the process obeys, and reflect this in the objective function in a certain way.
Once again about energy as a target function - in Rosseta @ home for RNA, it was such
SCORE = (VDW * 3.0 + RG) + (RNA_BS + RNA_BP_W + RNA_BP_H + RNA_BP_S) + (RNA_NONB * 1.5 + RNA_O2ST + RNA_PHOS) + (RNA_AXIS * 0.2 + RNA_STAG * 0.5)
I will not decipher. But it is important that this is a certain sum of the contributions of the various supposed actions. The result is something arithmetic mean. And accordingly, we are moving towards something amorphous. No one will give exact coefficients at the parameters, what contribution a particular parameter makes. And it is impossible to calculate them - after all, we are building a target function. Guessing is also not the case. At first I tried - and found out that more than half simply does not make a serious contribution, but only rejects the calculations not where it is needed.
Therefore, I left at the beginning only VDW - this is a kind of generalized coefficient, in fact it shows whether there are forbidden covalent bonds (as discussed in the first articles). And over time, I replaced it with just the yes / no answer, because it happened that other parameters - sometimes they were outweighed - and as a result intersections were obtained in the .pdb file, which should not be.
Further, we remember that I proposed to base only on the formation of hydrogen bonds. When they are formed we know mathematically without any far-fetched things: distance and angle are everything. Where in the RNA they are - we also consistently know. (more precisely, it is now quite well predicted, there are nuances - but then).
In the figure, the secondary structure of a single ribozyme, which I took for experiments

To simplify my life, I began with the already existing hypothesis that RNA / proteins fold up hierarchically: the so-called Hierarchical model, which has a number of variations, but the essence is this: first, begin to form elements of the secondary structure in the expanded chain. If we focus on the word “begin”, then this is a completely normal hypothesis, but sometimes it is understood in such a way that secondary structures are fully formed, and only then does further folding occur. This is somewhat incorrect. But it will be important for us later, when we completely turn off the ribozyme (I’ll say right away, I haven’t finally succeeded in it - according to my criteria, but they turned out to be tougher, because I do not base on energy, where it’s not clear that the minimum is reached or can be even better But I seem to be close to the decision.).
And now let's turn at least a small area, form hydrogen bonds between the two nucleotides. Take the right loop cugacgucg (from 14 to 22) - 9 nucleotides and form a hydrogen bond between the extreme cg.
How to build a target function?
Three hydrogen bonds are formed between cg, so we have three distances (r1, r2, r3) and three angles (a1, a2, a3). In order for the function to be speaking, we need to be like this: if its value is finally zero and less, then all 3 hydrogen bonds are formed. A positive value should smoothly show an approximation to this state.
Therefore, it is necessary to subtract 3 agstroms from current distances, and 20 degrees from angles. We obtain the values that make a positive contribution to the function. I would like to spit all these 3 corners and 3 distances - and get the value of the objective function. But the distances and angles are not serious, different values. Therefore, there is such a method of reduction to the same scale. Significant distances (after subtracting 3) are somewhere between 1 and 12. Significant in the sense that the angle already affects these distances. And if the distance is greater, then the angle is not important: what difference does it make if atoms are turned, if a chasm separates them. And we have angles from 0 to 180, minus 20 = 160.
If you estimate roughly it turns out that if you multiply the distance by 10, then the distances and angles will be on the same scale. Therefore, we do:
r1 - = 3.0f; r1 * = 10;
r2 - = 3.0f; r2 * = 10;
r3 - = 3.0f; r3 * = 10;
a1 - = 20;
a2 - = 20;
a3 - = 20;
Next, there are two options. One
locScore = (r1 + r2 + r3 + a1 + a2 + a3)
and second
if (maxR> maxA)
{locScore = maxR; }
else
{locScore = maxA; }
where maxR = maximum from (r1, r2, r3), and maxA = maximum from (a1, a2, a3)
Each of the options is good in its own way. To start folding good second. After having already a rough structure, the first one can come in handy.
Well, the algorithm is very simple: we begin to rotate (in part 3 - we remember that we have selected 1500 possible turns) nucleotides with numbers
14
15
sixteen
17
18 - for example, it is here that the turn with number 210 is the best among all
nineteen
20
21
22
rotate say two angles №1 and №6 (i.e. №16). Finding the best fix. Our little chain will fold in two. After some time, we pound the “tension” in such a way (the left and right ends tend to connect, and the loop is under stress) our chain, that in corners 1 and 6 it stops rotating, and the algorithm loops. As soon as it ceases to give the best state, we change the combination of angles, for example, 3 and 4 (No. 34), etc. This will gradually relieve the voltage in corners 1 and 6, and then you can try to “compress” it.
This algorithm is quite enough for the required hydrogen bond to form.
In the next article of the second season :) let's talk about what difficulties appear in the formation of the entire spiral. But still one spiral.
PS I am very glad that serious comments appeared on the third article. But at the same time it looks like a philistine, a potential FoldIt player or simply supporting bio. distributed computing loses interest. I told some completed part (Hello, RNA World). Further it will not be more difficult, but perhaps the details of the rest are not so interested in the inhabitants (write, if this is not so). I do not deny that I am looking for like-minded people and those with whom you can test hypotheses, but at the same time I am not ready for mass, and the software is also not ready. In general, to whom it is not indifferent to write, then I will soon ripen for the season number two.
An important question for mathematicians :
Above, I described two objective functions.
1. locScore = (r1 + r2 + r3 + a1 + a2 + a3)
2. if (maxR> maxA) {locScore = maxR; } else {locScore = maxA; }
Do you know how to combine them into one? Those. let's say if the first objective function was used 5 times, then the second one was used 5 times and a certain result was obtained (lowering the “energy”). It is necessary that the function obtained after the merge, after its application 5 times, would give the same result as if to apply the first and second in turn. Is it possible?
Source: https://habr.com/ru/post/140211/
All Articles