Part number 3. Biochemistry on folding. How to reduce the number of turns the chain?
In this part we will talk about how you can reduce the number of turns of the chain so as to reduce the calculations, but without losing the possibility of falling into the necessary states.
But first I want to contact specialists in this area:
First, I will dispel a possible misunderstanding: I am an amateur, and I do not deal with this topic professionally. I noticed that there are experts in this topic. It is strange that I do not read your articles, and you read mine. I really hope that this situation will change. I want to read your articles, and preferably written in simple language, and where you give answers, rather than send in a known direction to Google. I just have a certain negative experience when I just started a number of specialists who could be found on the Internet, they made a smart look and did not help in word and deed - they sent in the indicated direction. Here I try to tell my little experience - but maybe it will allow someone easier to start.
')
But those who wish to cheer here. Let's do this. I am such an amateur - to whom the epaulettes of experts mean little, but science such a thing requires repeatability (and not business secrecy, is it not business to hide the details of its algorithms and not publish their code?), So I’m just interested in conversations a little. But I am very interested in when they show me that I’m doing a little wrong, and that there are people who have really achieved something. Here is the task I'm suffering. Decide and show that this is easy - I will be very grateful.
I give an arbitrary (really existing) primary sequence up to 100 nucleotides. I specify all hydrogen bonds that need to be formed. You give me the output .pdb file, in which the tertiary structure from the specified primary sequence and where all the required hydrogen bonds are formed. No other requirements.
I ask or show that it is simply or responsibly to confirm that this task, say for a week (or another reasonable time), is not solved.
Well, for now this is not and there are no your articles, for example, on other approaches, such as molecular dynamics, etc., if you please read about the approach I have proposed and criticize constructively , help your knowledge, participate in the discussion of the problem and can even be combined with me efforts and do something together.
And again to my audience, which is not experts : it is important to believe that it is easy, and it is not necessary to know physics, biology, and complex mathematics - I hope you can program and this is enough. Above, by the way, the task that we will solve ... but not all at once. By pluses - I understood what you read. But is everything clear and there are no questions? If I wait for comments, even the most naive. It is time to make this area of research at least as simple as the description, and not to hide it behind unnecessary tones of difficulties.
So. Today, the plan is simple - it is necessary to reduce reasonably the number of turns that we will calculate. There are two ways (not at all, but in my cybernetic-geometric approach).
Method number 1. Relatively simple. In general, if you rotate with an accuracy of 0.1 degrees, that is, 3600 variants of rotation. But as a rule, when the chain already has several hydrogen bonds, it does not have much freedom of rotation. Therefore, you can take from the current angle ± 5 degrees, and then you need to check only 100 options. If you need to turn more than 5 degrees, then this will happen at the next iteration.
The first method can be limitedly applied when the chain already has a number of hydrogen bonds, and has assumed a less or less correct state. If it is applied to the initial state of the chain - an elongated chain, then this method will very quickly lead to a local minimum. Remember in the first article of the 5 steps of folding the chain in the picture. So the chain will be rolled up to step 5, and then it will not be able to take a normal state, the algorithm will go in cycles.
Method number 2. This method was inspired by the Rhiju Das and David Baker article , “Automated de novo prediction of native-like RNA tertiary structures”, University of California, Berkeley, CA, 2007 . Over time, I have improved a little and am telling. Rhiju Das suggested an interesting idea. How is it advantageous to turn at several angles at once, so that the combination of these angles is advantageous? He decided to peep from nature, and this is very correct. Here it was described that a 3D model of the ribosome was obtained at the atomic level. So, the ribosome consists not only of proteins, but basically, as a platform on which proteins then fit, contains two ribosomal RNAs. One of them, the largest, contains 2700 nucleotides. It was obtained in a bio-experiment. Rhiju Das compiled a database of angles that are in this ribosome = 9 * 2700 angles. If we distinguish between purines (a, g) and pyrimidines (u, c), then we have approximately 1500 variants. Then let's say we want to rotate the combination of two corners No. 1 and No. 6 (let's briefly record 16) - take the appropriate 1500 corners from the database and rotate. And this surprisingly gives good results, although we turn a completely different RNA chain.
Further in the next article we will need to talk about the so-called. objective function, i.e. how to evaluate we made a good turn or not . Here my cybernetic approach is somewhat revolutionary. I have met everywhere that they are based only on the energy of the chain. Or calculating as closely as possible physically or doing a mathematical estimation.
Why did I go the other way? I give one slide first:
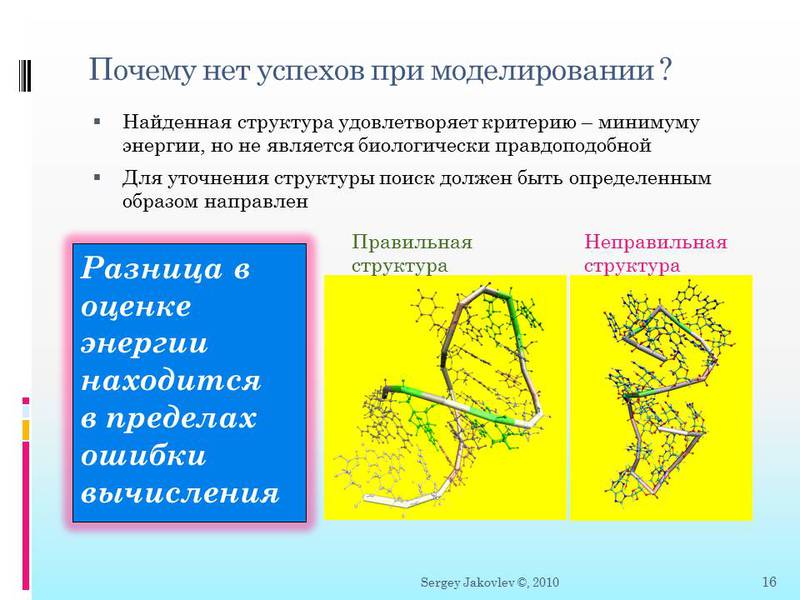
Of course this is somewhat exaggerated. But not far from the truth. You see two structures of the chain - the energy estimate for them gives very close values. But do you see how the structures are different? One is immediately visible in the picture - biologically implausible. That is why the visualization is very important here, the computer can do the calculations for a long time, considering something as a “good” state. But if calculations got into such a “biologically wrong” state, then there is practically no chance to stop the algorithm and get out of a local solution, switching to the worst in terms of energy evaluation, but more biologically correct. That is why in the game FoldIt a person has a greater chance than a computer machine. A person sees, roughly represents how a chain can be folded and will not search when he sees that he has fallen deep into a local minimum.
Just keep in mind that the assessment or even the physical calculation of energy is quite long, difficult - but the main difference between the biologically possible and the biologically insolvent structure is within the limits of the calculation error.
And this is a problem. Specialists here with me probably begin to argue - bring specific data, do not waste my time on holivar.
Therefore, in my article I write:
I have illustrated the first point above. The failure of the pure Monte Carlo method, as well as algorithms in which similar ones occur - for example, genetic algorithms, Q-learning, gradient searches, etc. - we will discuss at will - this is not a central theme for me. But I think if you think you will understand that by chance choosing a state in a field in which there is only one cleft, you will fall into small puddles in 99% percent and look for a cleft in it, and you will not find it. And in order to find a crevice with a random choice, you need to make a choice as many times as there are stages and with full enumeration. And then build a good face on a bad game?
In the next part, I will describe how I propose to make an assessment of the state of the chain, and how to search, i.e. let's approach the search algorithm itself.
But first I want to contact specialists in this area:
First, I will dispel a possible misunderstanding: I am an amateur, and I do not deal with this topic professionally. I noticed that there are experts in this topic. It is strange that I do not read your articles, and you read mine. I really hope that this situation will change. I want to read your articles, and preferably written in simple language, and where you give answers, rather than send in a known direction to Google. I just have a certain negative experience when I just started a number of specialists who could be found on the Internet, they made a smart look and did not help in word and deed - they sent in the indicated direction. Here I try to tell my little experience - but maybe it will allow someone easier to start.
')
But those who wish to cheer here. Let's do this. I am such an amateur - to whom the epaulettes of experts mean little, but science such a thing requires repeatability (and not business secrecy, is it not business to hide the details of its algorithms and not publish their code?), So I’m just interested in conversations a little. But I am very interested in when they show me that I’m doing a little wrong, and that there are people who have really achieved something. Here is the task I'm suffering. Decide and show that this is easy - I will be very grateful.
I give an arbitrary (really existing) primary sequence up to 100 nucleotides. I specify all hydrogen bonds that need to be formed. You give me the output .pdb file, in which the tertiary structure from the specified primary sequence and where all the required hydrogen bonds are formed. No other requirements.
I ask or show that it is simply or responsibly to confirm that this task, say for a week (or another reasonable time), is not solved.
Well, for now this is not and there are no your articles, for example, on other approaches, such as molecular dynamics, etc., if you please read about the approach I have proposed and criticize constructively , help your knowledge, participate in the discussion of the problem and can even be combined with me efforts and do something together.
And again to my audience, which is not experts : it is important to believe that it is easy, and it is not necessary to know physics, biology, and complex mathematics - I hope you can program and this is enough. Above, by the way, the task that we will solve ... but not all at once. By pluses - I understood what you read. But is everything clear and there are no questions? If I wait for comments, even the most naive. It is time to make this area of research at least as simple as the description, and not to hide it behind unnecessary tones of difficulties.
So. Today, the plan is simple - it is necessary to reduce reasonably the number of turns that we will calculate. There are two ways (not at all, but in my cybernetic-geometric approach).
Method number 1. Relatively simple. In general, if you rotate with an accuracy of 0.1 degrees, that is, 3600 variants of rotation. But as a rule, when the chain already has several hydrogen bonds, it does not have much freedom of rotation. Therefore, you can take from the current angle ± 5 degrees, and then you need to check only 100 options. If you need to turn more than 5 degrees, then this will happen at the next iteration.
The first method can be limitedly applied when the chain already has a number of hydrogen bonds, and has assumed a less or less correct state. If it is applied to the initial state of the chain - an elongated chain, then this method will very quickly lead to a local minimum. Remember in the first article of the 5 steps of folding the chain in the picture. So the chain will be rolled up to step 5, and then it will not be able to take a normal state, the algorithm will go in cycles.
Method number 2. This method was inspired by the Rhiju Das and David Baker article , “Automated de novo prediction of native-like RNA tertiary structures”, University of California, Berkeley, CA, 2007 . Over time, I have improved a little and am telling. Rhiju Das suggested an interesting idea. How is it advantageous to turn at several angles at once, so that the combination of these angles is advantageous? He decided to peep from nature, and this is very correct. Here it was described that a 3D model of the ribosome was obtained at the atomic level. So, the ribosome consists not only of proteins, but basically, as a platform on which proteins then fit, contains two ribosomal RNAs. One of them, the largest, contains 2700 nucleotides. It was obtained in a bio-experiment. Rhiju Das compiled a database of angles that are in this ribosome = 9 * 2700 angles. If we distinguish between purines (a, g) and pyrimidines (u, c), then we have approximately 1500 variants. Then let's say we want to rotate the combination of two corners No. 1 and No. 6 (let's briefly record 16) - take the appropriate 1500 corners from the database and rotate. And this surprisingly gives good results, although we turn a completely different RNA chain.
Further in the next article we will need to talk about the so-called. objective function, i.e. how to evaluate we made a good turn or not . Here my cybernetic approach is somewhat revolutionary. I have met everywhere that they are based only on the energy of the chain. Or calculating as closely as possible physically or doing a mathematical estimation.
Why did I go the other way? I give one slide first:

Of course this is somewhat exaggerated. But not far from the truth. You see two structures of the chain - the energy estimate for them gives very close values. But do you see how the structures are different? One is immediately visible in the picture - biologically implausible. That is why the visualization is very important here, the computer can do the calculations for a long time, considering something as a “good” state. But if calculations got into such a “biologically wrong” state, then there is practically no chance to stop the algorithm and get out of a local solution, switching to the worst in terms of energy evaluation, but more biologically correct. That is why in the game FoldIt a person has a greater chance than a computer machine. A person sees, roughly represents how a chain can be folded and will not search when he sees that he has fallen deep into a local minimum.
Just keep in mind that the assessment or even the physical calculation of energy is quite long, difficult - but the main difference between the biologically possible and the biologically insolvent structure is within the limits of the calculation error.
And this is a problem. Specialists here with me probably begin to argue - bring specific data, do not waste my time on holivar.
Therefore, in my article I write:
the Monte Carlo method is used to select the position and angles of rotation from a discrete set, the rotation is performed, and on the basis of an estimate of the energy function, it is decided whether this rotation contributes to stacking in a stable state. If the energy goes down, then it contributes, and then we proceed from this state. If not, the turn is canceled. So
Thus, several million random turns are performed, after which a tertiary structure with a minimum energy estimate is obtained, which is a model of the corresponding RNA.
In similar computer experiments, the discretization method may vary.
turns and accuracy of the energy estimation function, but the search principles remain the same. But
When using the above approach, there are two significant drawbacks:
1. The energy estimation function is approximate, the values of which may be within
calculation errors.
2. The probability on a multidimensional energy surface to get into the global energy minimum is so low that it is comparable to a full search. In this way,
using the Monte Carlo method to select turns that should be checked, in fact
brute force is carried out only in random order. And that makes no sense for NP-
complete task.
I have illustrated the first point above. The failure of the pure Monte Carlo method, as well as algorithms in which similar ones occur - for example, genetic algorithms, Q-learning, gradient searches, etc. - we will discuss at will - this is not a central theme for me. But I think if you think you will understand that by chance choosing a state in a field in which there is only one cleft, you will fall into small puddles in 99% percent and look for a cleft in it, and you will not find it. And in order to find a crevice with a random choice, you need to make a choice as many times as there are stages and with full enumeration. And then build a good face on a bad game?
In the next part, I will describe how I propose to make an assessment of the state of the chain, and how to search, i.e. let's approach the search algorithm itself.
Source: https://habr.com/ru/post/140158/
All Articles