Fast 128-bit LFSR (MMX required)
Random numbers are a dark horse providing security mechanisms in a digital environment. Unjustly remaining in the shadow of cryptographic primitives, they are at the same time a key element for generating session keys, used in Monte Carlo numerical methods, in simulation modeling, and even to test the theories of the formation of cyclones!
At the same time, the quality of the implementation of the pseudo-random number generator itself depends on the quality of the resulting sequence. As the saying goes: "the generation of random numbers is too important to leave it to chance."

')
There are a lot of options for the implementation of a pseudo-random number generator: Yarrow, which uses traditional crypto-primitives, such as AES-256, SHA-1, MD5; Microsoft's CryptoAPI; exotic Chaos and PRAND and others.
But the purpose of this note is different. Here I want to consider the peculiarity of the practical implementation of one very popular pseudo-random number generator, which is widely used, for example, in the Unix environment in the / dev / random pseudo-device, as well as in electronics and in the creation of stream ciphers. It's about LFSR (Linear Feedback Shift Register) .
The fact is that there is an opinion that in the case of using dense polynomials, the state of the LFSR register is very slowly calculated. But as I see it, often the problem is not in the algorithm itself (although it is certainly not an ideal), but in its implementation.
Literally, LFSR is a linear feedback shift register consisting of two parts, the shift register and the feedback function. A register consists of bits; its length is the number of these bits.
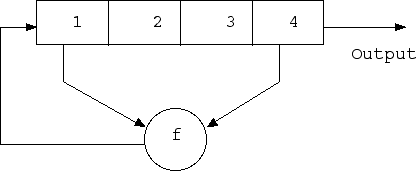
When a bit is extracted, all bits of the register are shifted to the right by one position. In this case, the new leftmost bit is determined by the function of the remaining bits before extraction. The output of the register is the least significant bit.
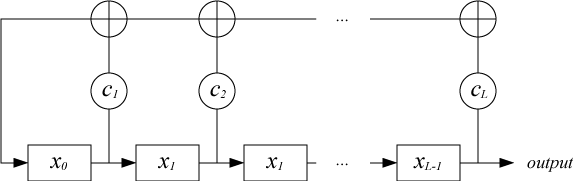
As it is not difficult to determine, the properties of the output sequence are closely related to the properties of the associated polynomial: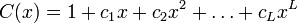
At the same time, its nonzero coefficients are called taps, on the basis of which the incoming values for the feedback function are determined.
Recommended tap indices depending on the length of the bit field of the LFSR register are well presented in the document “ Effiient Shift Registers, LFSR Counters, and Long Pseudo Random Sequence Generators ”.
So, the implementation of LFSR is quite simple, but it is believed that due to the use of many bit operations for rendering dense polynomials such as XOR, the speed of work often leaves much to be desired, i.e. he needs some time to warm up. As an alternative, a modification of the LFSR with a Galois scheme was proposed, in which a cycle of a fixed number of calls to the LFSR function in which is performed approximately twice as fast.
Honestly, I can not agree with that. As I see, often the problem is not in the algorithm itself, but in its implementation. Usually we see a structure of the following type:
Cruel. Here, at a minimum, we can get rid of several XOR and shifts using the parity flag value of the PF (Parity Flag) flag. Indeed, modulo 2 (XOR) additions determine the parity of the number of bits set. The only parity flag PF is set if the least significant byte of the result contains an even number of single (non-zero) bits, i.e. at least one arithmetic shift we still have to do:
In the case of using dense polynomials, when the taps are distributed over the entire bit field of the 32-bit register, then we will get 4 shift operations and 3 XOR operations:
Deviation: in the case when the number of shifts of sar ebx, 08h is even or equal to zero, before executing the XOR it is necessary to invert the value of the register AH, since PF is set when the number of nonzero bits is even. And we need the opposite.
What is still somewhat kosher than:
The next step is to use a register to accumulate the results, instead of directly dumping into memory on each LFSR state:
and so up to 32 states (edx DWORD), only after which we write to memory.
And finally, if we really need to implement a smart 128-bit LFSR (suddenly) we can use the MMX registers, which will allow us on the 32-bit Pentium processor to realize a shift without having to access the memory (only by means of registers).
Source
Source code in assembly language (x86): pastebin.com/rwKfsYsN
Compiled executable code: www.sendspace.com/file/atg0cf
Update:
Optimized version of the code: pastebin.com/B3kPEaew
Compiled executable code: www.sendspace.com/file/9bl5di
Finally, about the speed of work - “warming up” of the 128-bit LFSR through a shift of 2,097,120 (0FFFFh x 32) states using the MMX and register of flags with a coffee break (display) took on my PC about 5 seconds. At the same time, execution of the program in C ++, written by analogy with the above, but for the 128-bit version and also with the output to the screen, took about 2-3 minutes.
At the same time, the main factor is that in the case of using Parity Flag, the density of the polynomial does not have a strong effect on the speed of calculating the inverse function for the new state of the LFSR register. And accordingly, the statements in the style: “One of the main problems of the RSLOS is that their software implementation is extremely ineffective. You have to avoid sparse feedback polynomials as they lead to easier cracking by a correlation attack. And dense polynomials are very slowly calculated ”(from here: ru.wikipedia.org/wiki/LFSR ) are somewhat ... untenable and need to be clarified :)
ps And what’s interesting is, is it possible to make a program implementation in a high-level language, without assembly inserts, the execution time of which when iterating through 2,097,120 (0FFFFh x 32) states for 128-bit LFSR would take ... for example, less than 0.5 second?
At the same time, the quality of the implementation of the pseudo-random number generator itself depends on the quality of the resulting sequence. As the saying goes: "the generation of random numbers is too important to leave it to chance."

')
There are a lot of options for the implementation of a pseudo-random number generator: Yarrow, which uses traditional crypto-primitives, such as AES-256, SHA-1, MD5; Microsoft's CryptoAPI; exotic Chaos and PRAND and others.
But the purpose of this note is different. Here I want to consider the peculiarity of the practical implementation of one very popular pseudo-random number generator, which is widely used, for example, in the Unix environment in the / dev / random pseudo-device, as well as in electronics and in the creation of stream ciphers. It's about LFSR (Linear Feedback Shift Register) .
The fact is that there is an opinion that in the case of using dense polynomials, the state of the LFSR register is very slowly calculated. But as I see it, often the problem is not in the algorithm itself (although it is certainly not an ideal), but in its implementation.
Little about LFSR
Literally, LFSR is a linear feedback shift register consisting of two parts, the shift register and the feedback function. A register consists of bits; its length is the number of these bits.

When a bit is extracted, all bits of the register are shifted to the right by one position. In this case, the new leftmost bit is determined by the function of the remaining bits before extraction. The output of the register is the least significant bit.

As it is not difficult to determine, the properties of the output sequence are closely related to the properties of the associated polynomial:
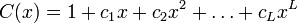
At the same time, its nonzero coefficients are called taps, on the basis of which the incoming values for the feedback function are determined.
Recommended tap indices depending on the length of the bit field of the LFSR register are well presented in the document “ Effiient Shift Registers, LFSR Counters, and Long Pseudo Random Sequence Generators ”.
Practical implementation
So, the implementation of LFSR is quite simple, but it is believed that due to the use of many bit operations for rendering dense polynomials such as XOR, the speed of work often leaves much to be desired, i.e. he needs some time to warm up. As an alternative, a modification of the LFSR with a Galois scheme was proposed, in which a cycle of a fixed number of calls to the LFSR function in which is performed approximately twice as fast.
Honestly, I can not agree with that. As I see, often the problem is not in the algorithm itself, but in its implementation. Usually we see a structure of the following type:
int LFSR (void) { static unsigned long S = 0xFFFFFFFF; /* taps: 32 31 30 28 26 1; charact. polynomial: x^32 + x^31 + x^30 + x^28 + x^26 + x^1 + 1 */ S = ((( (S>>0)^(S>>1)^(S>>2)^(S>>4)^(S>>6)^(S>>31) ) & 1 ) << 31 ) | (S>>1); return S & 1; } Cruel. Here, at a minimum, we can get rid of several XOR and shifts using the parity flag value of the PF (Parity Flag) flag. Indeed, modulo 2 (XOR) additions determine the parity of the number of bits set. The only parity flag PF is set if the least significant byte of the result contains an even number of single (non-zero) bits, i.e. at least one arithmetic shift we still have to do:
xor ecx,ecx mov ebx,0FFFFFFFFh ; S mov eax,080000057h ; taps (32,31,30,28,26,1) and ebx,eax mov cl,ah sar ebx,018h lahf xor cl,ah sar cl,02h and cl,01h In the case of using dense polynomials, when the taps are distributed over the entire bit field of the 32-bit register, then we will get 4 shift operations and 3 XOR operations:
xor ecx,ecx mov ebx,0FFFFFFFFh ; S mov eax,095324C57h ; taps (32,31,30,28,26,22,21,18,15,12,11,8,6,4,1) and ebx,eax lahf mov cl,ah ; [0-7] bits sar ebx,08h lahf xor cl,ah ; [8-15] bits sar ebx,08h lahf xor cl,ah ; [16-23] bits sar ebx,08h lahf xor cl,ah ; [24-31] bits sar cl,02h and cl,01h Deviation: in the case when the number of shifts of sar ebx, 08h is even or equal to zero, before executing the XOR it is necessary to invert the value of the register AH, since PF is set when the number of nonzero bits is even. And we need the opposite.
What is still somewhat kosher than:
int LFSR (void) { static unsigned long S = 0xFFFFFFFF; S = ((( (S>>0)^(S>>1)^(S>>2)^(S>>4)^(S>>6)^(S>>10)^(S>>11)^ (S>>14)^(S>>17)^(S>>20)^(S>>21)^(S>>24)^(S>>26)^ (S>>28)^(S>>31) ) & 1 ) << 31 ) | (S>>1); return S & 1; } The next step is to use a register to accumulate the results, instead of directly dumping into memory on each LFSR state:
sal edx,01h or dl,cl and so up to 32 states (edx DWORD), only after which we write to memory.
And finally, if we really need to implement a smart 128-bit LFSR (suddenly) we can use the MMX registers, which will allow us on the 32-bit Pentium processor to realize a shift without having to access the memory (only by means of registers).
Source
Source code in assembly language (x86): pastebin.com/rwKfsYsN
Compiled executable code: www.sendspace.com/file/atg0cf
Update:
Optimized version of the code: pastebin.com/B3kPEaew
Compiled executable code: www.sendspace.com/file/9bl5di
- 128-bit LFSR
- MMX registers are used
- x86 architecture
- change 2097120 (0FFFFh x 32) state register LFSR
Eventually
Finally, about the speed of work - “warming up” of the 128-bit LFSR through a shift of 2,097,120 (0FFFFh x 32) states using the MMX and register of flags with a coffee break (display) took on my PC about 5 seconds. At the same time, execution of the program in C ++, written by analogy with the above, but for the 128-bit version and also with the output to the screen, took about 2-3 minutes.
At the same time, the main factor is that in the case of using Parity Flag, the density of the polynomial does not have a strong effect on the speed of calculating the inverse function for the new state of the LFSR register. And accordingly, the statements in the style: “One of the main problems of the RSLOS is that their software implementation is extremely ineffective. You have to avoid sparse feedback polynomials as they lead to easier cracking by a correlation attack. And dense polynomials are very slowly calculated ”(from here: ru.wikipedia.org/wiki/LFSR ) are somewhat ... untenable and need to be clarified :)
ps And what’s interesting is, is it possible to make a program implementation in a high-level language, without assembly inserts, the execution time of which when iterating through 2,097,120 (0FFFFh x 32) states for 128-bit LFSR would take ... for example, less than 0.5 second?
Source: https://habr.com/ru/post/140095/
All Articles