The basics of social network analysis (Social Network Analysis 101)
From the translator. The author of this publication is Michael Wu ( Michael Wu ), a leading analyst at Lithium , specializing in the study of social interactions and online communities.
To understand what a “social network analysis” ( Social Network Analysis , SNA) is, you need to understand what a “social network” is and what a “social graph” is. Simply put, social network analysis is a way to study social networks, and a social network is a set of entities between which there are certain relationships. Social networks have been around since people started roaming the earth. In truth, not only humans have such structures, but also social animals (for example, wolves, lions, dolphins, mice, and even ants).
Of course, above all, we are interested in such entities as people, and such relations between them as friendship (like on Facebook), collaboration (like on LinkedIn), kinship, communication and some other social interactions. And in the context of SNA, we can understand as a social graph simply the visualization of all this (I am not going to bore me with the formal definition of a graph ). In such a social graph, each point (or node, or vertex) represents a person, and the edge between two points (people) represents the relationship between them. And since there are many different relationships between people, there are also many different social graphs depicting these relationships. I will show it with a specific example.
Let's assume that I, Michael, have a very small social network consisting of just seven friends (see Figure 1). Suppose further that I have a very simple life, in which I support only three types of social relations: I have work colleagues (indicated by red edges), drinking companions (blue edges) and badminton partners (green edges).
')
What is my social life like? I have colleagues in Lithium (Phil and Joe, who are also colleagues for each other). And before I came to work in Lithium, I worked with Jack and Ryan at the University of California at Berkeley. Before that, I worked with Ryan and Don at the National Library of Los Alamos. Ryan came to Berkeley with me to receive the degree of Candidate of Science ( PhD ), so we crossed with him in two jobs. That's why Ryan also worked with Jack and Don, but who are not colleagues for each other.
Another part of my social life is connected with my drinking companions. I often went to drink with Doug, Adam and Ryan during graduate school. However, Ryan and Doug never stayed alone with each other and never went anywhere together. When I came to Lithium, I found out that Phil and Jack often drink together, but I have never done this with any of them.
Finally, I love badminton. Wherever I worked, I found a badminton partner. I played with Joe in Litium, with Jack at Berkeley, and with Don at Los Alamos. Ryan also plays badminton - with Phil and Doug. However, they play much better than me, so I have never played with any of them.
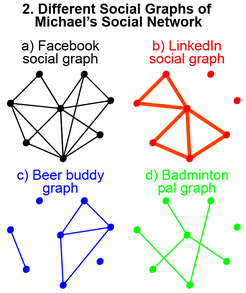If you imagine all my seven friends on Facebook, then our graph of friendship would look like that shown in Figure 2a. Black edges designate friendship, and more precisely people who are familiar with each other. But if you want to see my professional network, then my social graph will look like Figure 2b. In this case, the red edges indicate my relationship with colleagues. Please note that Adam and Doug are not included in my professional network (there are no red edges between us), because we have never worked together.
The graph of my drinking companions is shown in Figure 2c (where the blue ribs signify the fact that we drink together) and includes Doug, Adam and Ryan, since I never had a drink with any of my other friends. And despite the fact that Jack and Phil drink together, I never did it with them, so there are no blue ribs between us. Thus, Jack and Phil find themselves in a completely separate network of drinkers.
Finally, the graph of my badminton partners is shown in Figure 2d, where the green faces represent relationships based on the badminton playing together. Only Jack, Jo and Don are included in my badminton net. Ryan has his own network of Phil and Doug, and none of them is on my network.
Notice, we built four different social graphs from the same social network of eight people. By asking what the faces will denote, we get our own special graph with its special metrics. For example, if we decide that the edges should indicate a joint fun pastime, we will build another, completely different social graph, which will look like the intersection of my earlboard graph and badminton partner graph (of course, working in Lithium also brings a lot of fun, but I Now I simplify everything). Thus, due to the fact that there are many different relationships between people, many different social graphs can be built.
Therefore, the most important thing to do before interpreting any social graph is to understand what type of relationship its faces indicate. This is perhaps even more important than understanding what the vertices mean. In SNA, entities designated by vertices will usually always be human, but 99% of all metrics of a graph will strongly depend on its faces. Therefore, if the measured ratio is changing, represented by the faces, the metrics will also change.
For example, the simplest metric of a graph is the degree of centrality ( degree centrality ), which shows how many connections there are at a vertex. So, in total there are 7 black faces (Figure 2a), i.e. I have 7 friends. There are only 5 red faces (Figure 2b), i.e. I have 5 colleagues. My degree of centrality on a graph of drinking companions is 3 (Figure 2c), I have only 3 drinking companions. The degree of centrality can be calculated for all people on the graph. For example, the degree of centrality of Ryan on the badminton partners graph is 2 (Figure 2d).
Interpretation of graph metrics also depends on the interrelation of faces. So, we cannot find out about how many colleagues I have when looking at the graph of friends (Figure 2a), because relationships with work colleagues do not appear on the graph of friends. And even if we assume that everyone with whom I work becomes my friend, relying only on the graph of friends, we can only say that I can have any number of colleagues, from zero to seven. Therefore, never draw conclusions or conclusions about existing relationships, based on a graph in which these relationships are not expressed explicitly in its edges. In doing so, you will just read the tea leaves or make random assumptions.
In the following publications, using the example of specific live data, we will try to apply the methods of social network analysis to identify and measure social influence within social networks.
To understand what a “social network analysis” ( Social Network Analysis , SNA) is, you need to understand what a “social network” is and what a “social graph” is. Simply put, social network analysis is a way to study social networks, and a social network is a set of entities between which there are certain relationships. Social networks have been around since people started roaming the earth. In truth, not only humans have such structures, but also social animals (for example, wolves, lions, dolphins, mice, and even ants).
Of course, above all, we are interested in such entities as people, and such relations between them as friendship (like on Facebook), collaboration (like on LinkedIn), kinship, communication and some other social interactions. And in the context of SNA, we can understand as a social graph simply the visualization of all this (I am not going to bore me with the formal definition of a graph ). In such a social graph, each point (or node, or vertex) represents a person, and the edge between two points (people) represents the relationship between them. And since there are many different relationships between people, there are also many different social graphs depicting these relationships. I will show it with a specific example.
Representative social network and its social graph
Let's assume that I, Michael, have a very small social network consisting of just seven friends (see Figure 1). Suppose further that I have a very simple life, in which I support only three types of social relations: I have work colleagues (indicated by red edges), drinking companions (blue edges) and badminton partners (green edges).
')
What is my social life like? I have colleagues in Lithium (Phil and Joe, who are also colleagues for each other). And before I came to work in Lithium, I worked with Jack and Ryan at the University of California at Berkeley. Before that, I worked with Ryan and Don at the National Library of Los Alamos. Ryan came to Berkeley with me to receive the degree of Candidate of Science ( PhD ), so we crossed with him in two jobs. That's why Ryan also worked with Jack and Don, but who are not colleagues for each other.Another part of my social life is connected with my drinking companions. I often went to drink with Doug, Adam and Ryan during graduate school. However, Ryan and Doug never stayed alone with each other and never went anywhere together. When I came to Lithium, I found out that Phil and Jack often drink together, but I have never done this with any of them.
Finally, I love badminton. Wherever I worked, I found a badminton partner. I played with Joe in Litium, with Jack at Berkeley, and with Don at Los Alamos. Ryan also plays badminton - with Phil and Doug. However, they play much better than me, so I have never played with any of them.
If you imagine all my seven friends on Facebook, then our graph of friendship would look like that shown in Figure 2a. Black edges designate friendship, and more precisely people who are familiar with each other. But if you want to see my professional network, then my social graph will look like Figure 2b. In this case, the red edges indicate my relationship with colleagues. Please note that Adam and Doug are not included in my professional network (there are no red edges between us), because we have never worked together.The graph of my drinking companions is shown in Figure 2c (where the blue ribs signify the fact that we drink together) and includes Doug, Adam and Ryan, since I never had a drink with any of my other friends. And despite the fact that Jack and Phil drink together, I never did it with them, so there are no blue ribs between us. Thus, Jack and Phil find themselves in a completely separate network of drinkers.
Finally, the graph of my badminton partners is shown in Figure 2d, where the green faces represent relationships based on the badminton playing together. Only Jack, Jo and Don are included in my badminton net. Ryan has his own network of Phil and Doug, and none of them is on my network.
Reading and interpreting the social graph
Notice, we built four different social graphs from the same social network of eight people. By asking what the faces will denote, we get our own special graph with its special metrics. For example, if we decide that the edges should indicate a joint fun pastime, we will build another, completely different social graph, which will look like the intersection of my earlboard graph and badminton partner graph (of course, working in Lithium also brings a lot of fun, but I Now I simplify everything). Thus, due to the fact that there are many different relationships between people, many different social graphs can be built.
Therefore, the most important thing to do before interpreting any social graph is to understand what type of relationship its faces indicate. This is perhaps even more important than understanding what the vertices mean. In SNA, entities designated by vertices will usually always be human, but 99% of all metrics of a graph will strongly depend on its faces. Therefore, if the measured ratio is changing, represented by the faces, the metrics will also change.
For example, the simplest metric of a graph is the degree of centrality ( degree centrality ), which shows how many connections there are at a vertex. So, in total there are 7 black faces (Figure 2a), i.e. I have 7 friends. There are only 5 red faces (Figure 2b), i.e. I have 5 colleagues. My degree of centrality on a graph of drinking companions is 3 (Figure 2c), I have only 3 drinking companions. The degree of centrality can be calculated for all people on the graph. For example, the degree of centrality of Ryan on the badminton partners graph is 2 (Figure 2d).
Interpretation of graph metrics also depends on the interrelation of faces. So, we cannot find out about how many colleagues I have when looking at the graph of friends (Figure 2a), because relationships with work colleagues do not appear on the graph of friends. And even if we assume that everyone with whom I work becomes my friend, relying only on the graph of friends, we can only say that I can have any number of colleagues, from zero to seven. Therefore, never draw conclusions or conclusions about existing relationships, based on a graph in which these relationships are not expressed explicitly in its edges. In doing so, you will just read the tea leaves or make random assumptions.
In the following publications, using the example of specific live data, we will try to apply the methods of social network analysis to identify and measure social influence within social networks.
Source: https://habr.com/ru/post/139911/
All Articles