Once again about the skiplist ...

... or how I got "Alenka" for the console application

There is a fairly common opinion that performing various test tasks helps to very quickly raise your professional level. I myself sometimes like to dig out a tricky test thread and solve it in order to be constantly in good shape, as they say. I once performed a competitive task for an internship at one company, the task seemed to me amusing and interesting, here is its short text:

Imagine that your colleague-whiner came to talk about his difficult task - he needed not only to sort the set of integers in ascending order, but to give all the elements of an ordered set from L th to R th inclusive!
You stated that this is an elementary task and you need ten minutes to write a solution in C #. Well, or an hour. Or two. Or chocolate "Alenka"

It is assumed that duplicates are allowed in the set, and the number of elements will be no more than 10 ^ 6.

There are several comments on the evaluation of the decision:
')

Your code will be evaluated and tested by three programmers:

• Bill will run your solution on tests no larger than 10Kb.
• In Steven’s tests, the number of requests will be no more than 10 ^ 5, while the number of requests for addition will be no more than 100.
• In Mark tests, the number of queries will be no more than 10 ^ 5.

The solution can be very interesting, so I found it necessary to describe it.

Decision

Suppose we have an abstract repository.

Denote by Add (e) to add an item to the repository, and Range (l, r) to take a slice from l to r element.

The trivial version of the repository may be:

• The storage base will be an ordered, ascending dynamic array.
• Each time you insert a binary search is the position in which you want to insert an element.
• When requesting Range (l, r), we will simply take an array slice from l through r.

We estimate the complexity of the approach based on a dynamic array.

C Range (l, r) - taking a slice can be estimated as O (r - l).

C Add (e) - insertion in the worst case will work for O (n), where n is the number of elements. When n ~ 10 ^ 6, the insertion is a bottleneck. Below in the article will be proposed an improved version of the repository.

An example of the source code can be found here .

A more suitable option may be, for example:

• The basis of the repository will be a self-balancing search tree , having O (ln n) complexity for insert, search, delete operations (AVL tree, RB tree and others).
• The data structure is expanded by adding to the node information about the number of nodes in the subtree. This is necessary in order to get the i-th element of the tree for O (ln n).
• The addition of an element in the tree is rewritten to recalculate the number of nodes in the subtree. This can be done so that the cost of the add operation remains O (ln n).

I’ve almost gotten ready to open Kormen and start remembering how the RB-tree works, but I stumbled upon an article about SkipList on Wikipedia .

Skiplist

Skiplist is a randomized alternative to search trees based on several linked lists. It was invented by William Pugh in 1989. Searches, inserts and deletes are performed in logarithmically random time.

This data structure is not widely known (by the way, it is written quite clearly about it in Habré ), although it has good asymptotic estimates. Curiosity for the sake of it wanted to implement, the more there was a suitable task.

Then I will give a brief squeeze from all sources that I used to solve.

Suppose we have a sorted single-linked list:

In the worst case, the search is performed in O (n). How can you speed it up?

In one of the video lectures, which I reviewed when I was working on the puzzle, I gave a wonderful example about express lines in New York:

• High-speed lines connect some stations.
• Normal lines connect all stations.
• There are regular lines between common high-speed line stations.

The idea is as follows: we can add a certain number of levels with a certain number of nodes in them, while the nodes in the levels should be evenly distributed. Consider an example where half of the elements from the lower level are located on each of the upper levels:


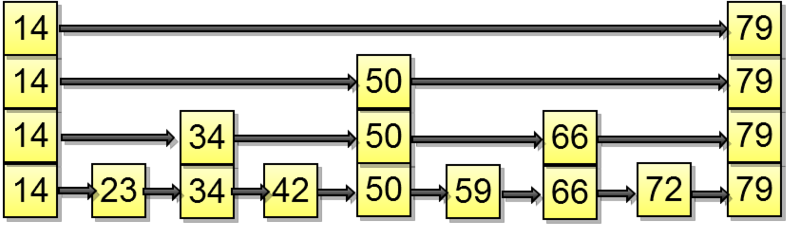
The example shows the perfect SkipList, in reality it looks like this, but a little bit wrong :)

Search

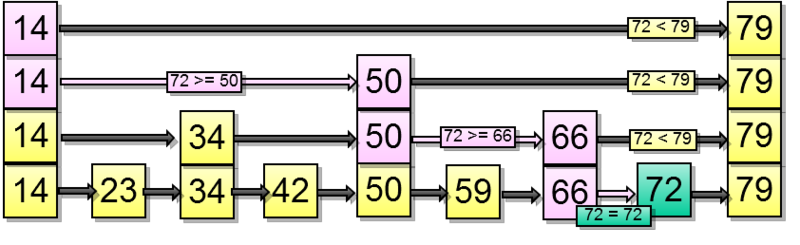
This is the search. Suppose we are looking for the 72nd element:

Insert

With an insert all is a little more difficult. In order to insert an element, we need to understand where to insert it in the lowest list and at the same time push it through to some number of higher levels. But how many levels should each specific element be pushed through?

It is proposed to solve this in the following way: when inserting, we add a new element to the lowest level and start throwing up a coin until it falls out, we push the element to the next higher level.
Let's try to insert an element - 67. First we find where to insert it in the list below:



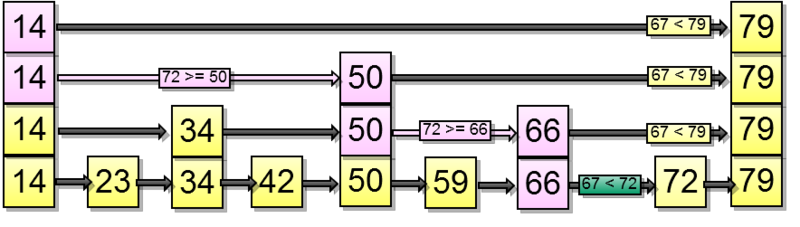
Supposed that the coin fell out twice in a row. So you need to push the element up two levels:

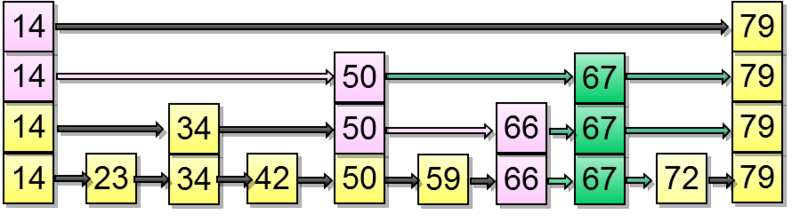
Access by index

To access by index it is proposed to do the following: mark each transition with the number of nodes that lies under it:



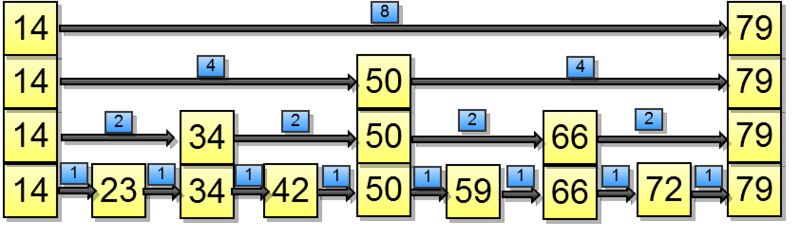
After we get access to the ith element (by the way, we get it for O (ln n)), it is not difficult to make the cut.

Let it be necessary to find Range (5, 7). First we get the element at index five:


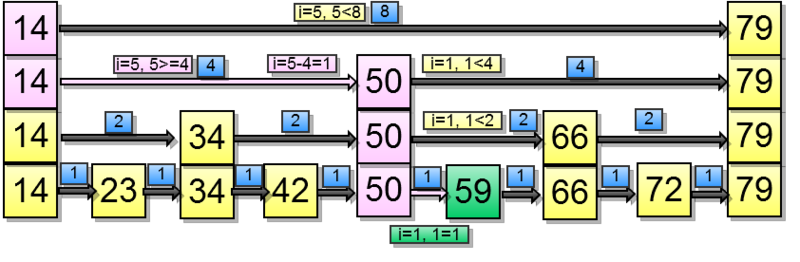
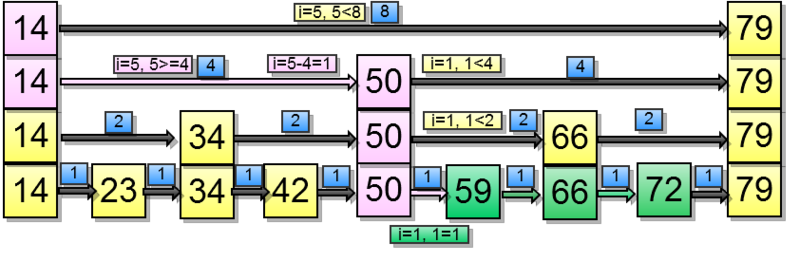
And now Range (5, 7):

About implementation

It seems a natural implementation when the SkipList node looks like this:

SkipListNode {
int Element;
SkipListNode[] Next;
int [] Width;
}


Actually, it is made in the implementation on the C from William Pug .

But in C #, its length is also stored in the array, and I wanted to do it for as little memory as possible (as it turned out, in the conditions of the task, everything was not assessed so strictly). At the same time, I wanted to make the implementation of SkipList and extended RB Tree occupy approximately the same amount of memory.

The answer to how to reduce memory consumption was unexpectedly found upon closer inspection of the ConcurrentSkipListMap from the java.util.concurrent package.

Two-dimensional skiplist

Let there be a single-linked list of all elements in one dimension. In the second one there will be “express lines” for transitions with links to the lower level.

ListNode {
int Element;
ListNode Next;
}

Lane {
Lane Right;
Lane Down;
ListNode Node;
}

Unfair coin

Even to reduce memory consumption, you can use the "dishonest" coin: reduce the likelihood of pushing an item to the next level. The article by William Pugh considered a cut of several values ​​of the probability of pushing. When considering the values ​​of ½ and ¼ in practice, we obtained approximately the same search time with a decrease in memory consumption.

A bit about random number generation

Delving into the giblets of ConcurrentSkipListMap, noticed that random numbers are generated as follows:

int randomLevel() {
int x = randomSeed;
x ^= x << 13;
x ^= x >>> 17;
randomSeed = x ^= x << 5;
if ((x & 0x80000001) != 0)
return 0;
int level = 1;
while (((x >>>= 1) & 1) != 0) ++level;
return level;
}

More information about the generation of pseudo-random numbers using XOR can be found in this article . I did not notice a special increase in speed, so I did not use it.

The source of the resulting storage can be found here .

All together you can pick up from googlecode.com (project Pagination).

Tests

Three types of storage were used:

1. ArrayBased (dynamic array)
2. SkipListBased (SkipList with the ¼ parameter)
3. RBTreeBased (red-ebony: the implementation of my friend, who performed a similar task).

Three types of tests for insertion of 10 ^ 6 elements were carried out:

1. Sorted items ascending
2. Sorted by Descending Items
3. Random items

Tests were conducted on a machine with i5, 8gb ram, ssd and Windows 7 x64.
Results:

	Array	Rbtree	Skiplist
Random	127033 ms	1020 ms	1737 ms
Ordered	108 ms	457 ms	536 ms
Ordered by descending	256337 ms	358 ms	407 ms

Quite expected results. It can be seen that inserting into an array when an element is inserted somewhere, except at the end, is the slowest. At the same time, SkipList is slower than RBTree.

Measurements were also taken: how much each storage takes up in memory when 10 ^ 6 elements are inserted into it. A studio profiler was used, for simplicity, the following code was run:

var storage = ...
for ( var i = 0; i < 1000000; ++i)
storage.Add(i);


Results:

	Array	Rbtree	Skiplist
Total bytes allocated	8,389,066 bytes	24,000,060 bytes	23,985,598 bytes

Also quite expected results: the storage on the dynamic array took the least amount of memory, and SkipList and RBTree took about the same amount.

Happy End with Alenka

A colleague-whiner, according to the condition of the problem, lost a bar of chocolate to me. My decision was credited with the maximum score. I hope someone this article will be useful. If you have any questions - I will be glad to answer.

PS: I was on an internship at SKB Kontur. This is not to answer the same questions =)