Recommender systems: SVD Part I
We continue to talk about recommender systems. Last time we made the first attempt to determine the similarity between users and the similarity between products. Today we will come to the same task on the other hand - we will try to train the factors that characterize users and products. If Vasya from the previous post likes films about tractors and doesn't like films about pigs, and Peter, on the contrary, it would be great to learn to understand which films are “about piglets” and recommend them to Peter, and which films are “about tractors”, and recommend them to Vasya.
I remind once again (and, apparently, I will remind until the end of time) that we have a matrix consisting of ratings (likes, purchase facts, etc.) that users (matrix rows) assigned to products (matrix columns). Let's look at the matrix
In which are recorded known to us ratings. As a rule, one user will not be able to evaluate a significant proportion of products, and there will hardly be many products that a significant proportion of users are ready to evaluate. This means that the matrix R is sparse (sparse); Is it possible to use this somehow?
The main tool for us will be the so-called singular decomposition of the matrix R :
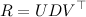
Singular decomposition is a fairly simple but very powerful tool. Actually, this is one of the main practical results of linear algebra, and the result is not very new (the properties of SVD were studied at the latest in the 1930s), and it is even more surprising when university courses in linear algebra are quite detailed. Some other aspects completely bypass the SVD side.
')
If you have three minutes, you can enjoy a vivid example of mathematical humor; humor, of course, is mathematic, so it's not that funny, but the essence is clearly stated, and the fans will surely like the music ... hmm, on a habr, it would probably be better to say that the fans of Fallout will like it:
In case there are still no three minutes, I will single out the property that is most important for us: if R is a large matrix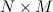
but of small rank f (in particular, sparse matrices are often of small rank), it can be decomposed into a product of the matrix 
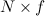and matrices 
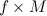thus sharply reducing the number of parameters, from NM to ( N + M ) f (to understand that this is a big progress, imagine that, as is usually the case in practice, N and M are measured in hundreds of thousands and millions, and f is less than ten ).
SVD is very widely used in machine learning; in fact, if you want to bring something closer, it is possible that SVD will meet you somewhere along the way. A classic example of using SVD is noise reduction, for example, in images. Consider a (black and white) image as a matrix of size X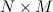 whose elements are the intensities of each pixel. Now we will try to select f columns of pixels from the image, find them “representative” and present each of the remaining columns as a linear combination of these. I will not go into mathematics right now, but as a result, when you find the optimal representations of each column, it turns out that you presented the original matrix in the form of a work 
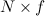size matrices and 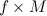, that is, they just approximated the matrix X with a matrix of small rank f .
The main property of SVD is that SVD gives the optimal approximation, if in matrix D you just leave exactly f of the first diagonal elements, and the rest are zero:
In the diagonal matrix D , which is in the middle of the singular value decomposition, the elements are ordered by size: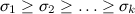
, so to nullify the last elements is to nullify the smallest elements.
If you choose a good f , then as a result, the image and weight will lose, and the noise on it will be less. And f in this case can be selected on the basis of the size of the singular values ​​of the matrix, i.e. those diagonal elements of the matrix D : it is desirable to discard as much as possible, but at the same time as small as possible of such elements.
But we digress. In the case of recommender systems, it turns out that we represent each user with a vector of f factors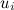
and present each product as a vector of f factors 
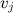and then, to predict the rating of user i to product j , we take their scalar product 
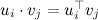. It can be said that a vector of user factors shows how much a user likes or dislikes a particular factor, and a vector of product factors shows how much one or another factor in a product is expressed. Linear algebra, on the other hand, tells us that for a sparse rating matrix such decomposition is often possible and has meaningful meaning.
It may turn out, by the way, that some factors will be easily understood by the human mind: for films, something like “comedy – drama”, “action share”, “romance share”, etc., can be distinguished, and the factors of users accordingly, they will show how appropriate the characteristics of the film to their taste. But nothing substantive can stand out - there are no guarantees here, formally we simply juggle with numbers.
Next time we will turn this basic idea - to bring the rating matrix of a small rank closer by SVD - into a well-posed optimization task and learn how to solve it.
I remind once again (and, apparently, I will remind until the end of time) that we have a matrix consisting of ratings (likes, purchase facts, etc.) that users (matrix rows) assigned to products (matrix columns). Let's look at the matrix
In which are recorded known to us ratings. As a rule, one user will not be able to evaluate a significant proportion of products, and there will hardly be many products that a significant proportion of users are ready to evaluate. This means that the matrix R is sparse (sparse); Is it possible to use this somehow?The main tool for us will be the so-called singular decomposition of the matrix R :
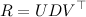
Singular decomposition is a fairly simple but very powerful tool. Actually, this is one of the main practical results of linear algebra, and the result is not very new (the properties of SVD were studied at the latest in the 1930s), and it is even more surprising when university courses in linear algebra are quite detailed. Some other aspects completely bypass the SVD side.
')
If you have three minutes, you can enjoy a vivid example of mathematical humor; humor, of course, is mathematic, so it's not that funny, but the essence is clearly stated, and the fans will surely like the music ... hmm, on a habr, it would probably be better to say that the fans of Fallout will like it:
In case there are still no three minutes, I will single out the property that is most important for us: if R is a large matrix
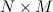but of small rank f (in particular, sparse matrices are often of small rank), it can be decomposed into a product of the matrix 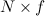and matrices 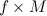thus sharply reducing the number of parameters, from NM to ( N + M ) f (to understand that this is a big progress, imagine that, as is usually the case in practice, N and M are measured in hundreds of thousands and millions, and f is less than ten ).SVD is very widely used in machine learning; in fact, if you want to bring something closer, it is possible that SVD will meet you somewhere along the way. A classic example of using SVD is noise reduction, for example, in images. Consider a (black and white) image as a matrix of size X
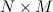whose elements are the intensities of each pixel. Now we will try to select f columns of pixels from the image, find them “representative” and present each of the remaining columns as a linear combination of these. 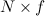I will not go into mathematics right now, but as a result, when you find the optimal representations of each column, it turns out that you presented the original matrix in the form of a work size matrices and 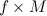, that is, they just approximated the matrix X with a matrix of small rank f .The main property of SVD is that SVD gives the optimal approximation, if in matrix D you just leave exactly f of the first diagonal elements, and the rest are zero:
In the diagonal matrix D , which is in the middle of the singular value decomposition, the elements are ordered by size:
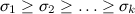, so to nullify the last elements is to nullify the smallest elements.If you choose a good f , then as a result, the image and weight will lose, and the noise on it will be less. And f in this case can be selected on the basis of the size of the singular values ​​of the matrix, i.e. those diagonal elements of the matrix D : it is desirable to discard as much as possible, but at the same time as small as possible of such elements.
But we digress. In the case of recommender systems, it turns out that we represent each user with a vector of f factors
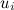and present each product as a vector of f factors 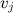and then, to predict the rating of user i to product j , we take their scalar product 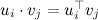. It can be said that a vector of user factors shows how much a user likes or dislikes a particular factor, and a vector of product factors shows how much one or another factor in a product is expressed. Linear algebra, on the other hand, tells us that for a sparse rating matrix such decomposition is often possible and has meaningful meaning.It may turn out, by the way, that some factors will be easily understood by the human mind: for films, something like “comedy – drama”, “action share”, “romance share”, etc., can be distinguished, and the factors of users accordingly, they will show how appropriate the characteristics of the film to their taste. But nothing substantive can stand out - there are no guarantees here, formally we simply juggle with numbers.
Next time we will turn this basic idea - to bring the rating matrix of a small rank closer by SVD - into a well-posed optimization task and learn how to solve it.
Source: https://habr.com/ru/post/139863/
All Articles