Container packing (bin packing) using a genetic algorithm
Good day, colleagues.
In this article, I continue the cycle dedicated to EvoJ - a Java framework for solving problems using a genetic algorithm.
In my previous post I introduced Habr's readers to the basic principles of working with EvoJ.
Today we will look at how using EvoJ can solve the problem of packing in containers.
If in a nutshell, the task of packing in containers is set as follows: there is a set of containers of a certain size, and a set of items that need to be packed in these containers (in the simplest case, spatial orientation is neglected). The goal is to pack all the items using as few containers as possible.
To use EvoJ, we must in some way describe the variable components of the solution of the problem in the form of a Java interface.
')
The first option is to describe each container as a list of items in it:
In essence, this is a list of containers, each of which is described by a list of parts that have fallen into it.
Despite the fact that EvoJ allows you to describe the solution in this way, this approach will force you to make additional efforts to screen out conflicting decisions when the same item falls into several containers.
A simpler approach will be to describe in which container each specific item fell:
Here the solution is presented as a list, each element of which indicates in which container the corresponding item fell.
This interface also demonstrates some of the EvoJ tricks. First, the length of the list, and the maximum value of its elements are not specified by specific numbers, but by the names of the variables. This allows you not to be tied to specific values in the compile-time.
Secondly, in this task, an important element is the indication
The number of occupied containers will be a natural fitness function, but this approach is not very effective. We illustrate why.
Solution 1
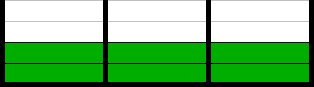
Solution 2

In both solutions, three containers are occupied. But it is obvious that the second solution is preferable, since it only has one mutation left before two containers become occupied. Of course, from the first solution, as a result of a mutation, a solution may appear where only two containers are occupied, but the probability of this is much lower.
Thus, the number of occupied containers is not enough to fully assess the "fitness" of the solution. To correct the situation, we introduce an additional indicator - the sum of squares of free space in containers (a simple sum of free space in both cases will be the same).
It may happen that some of the containers are overloaded. From our point of view, such a decision is not valid and it would be possible to get rid of such members of the gene pool by giving them a rating of
We introduce the third indicator to evaluate the solution - the sum of the squares of the overloads.
Thus, to adequately evaluate a solution, it takes three numbers. It would be possible to reduce them to some integral index, however, EvoJ allows to return any
Here the
The comparison procedure considers any decision without overload to be better than any solution to overload, if the overloads are equal, the occupied containers start to be taken into account (less is better), and finally, if the same number of containers are occupied, the
It remains to implement the fitness function. To do this, as in the examples from the previous article , expanding the AbstractSimpleRating class.
We will not analyze this code in detail; it simply calculates our fitness indicators and returns them as an instance of the
Create a new class with the
Here the
The size of the population and the number of iterations are chosen experimentally.
The code above is executed fairly quickly, and even 1000 iterations over a population of 200 solutions on my four-year laptop takes about two seconds.
We looked at how to apply the genetic algorithm to solving one of the classic NP-complex problems. It should be noted that the genetic algorithm does not guarantee finding the best solution, but allows you to get very close to it, which in most cases is sufficient.
For those interested , the source code of the considered example is laid out in the form of a Maven project.
Thanks for attention.
In this article, I continue the cycle dedicated to EvoJ - a Java framework for solving problems using a genetic algorithm.
In my previous post I introduced Habr's readers to the basic principles of working with EvoJ.
Today we will look at how using EvoJ can solve the problem of packing in containers.
Formulation of the problem
If in a nutshell, the task of packing in containers is set as follows: there is a set of containers of a certain size, and a set of items that need to be packed in these containers (in the simplest case, spatial orientation is neglected). The goal is to pack all the items using as few containers as possible.
Choosing a method for describing the solution
To use EvoJ, we must in some way describe the variable components of the solution of the problem in the form of a Java interface.
')
The first option is to describe each container as a list of items in it:
public interface Solution { List<List<Integer>> getContainers(); } In essence, this is a list of containers, each of which is described by a list of parts that have fallen into it.
Despite the fact that EvoJ allows you to describe the solution in this way, this approach will force you to make additional efforts to screen out conflicting decisions when the same item falls into several containers.
A simpler approach will be to describe in which container each specific item fell:
public interface Solution { @ListParams(length = "itemsCount", elementRange = @Range(strict = "true", min = "0", max = "lastBinIndex"), elementMutationRange = @MutationRange(value = "100%")) List<Integer> getBinIndices(); } Here the solution is presented as a list, each element of which indicates in which container the corresponding item fell.
This interface also demonstrates some of the EvoJ tricks. First, the length of the list, and the maximum value of its elements are not specified by specific numbers, but by the names of the variables. This allows you not to be tied to specific values in the compile-time.
Secondly, in this task, an important element is the indication
MutationRange=100% . Recall that in the list are the numbers of containers, and if you leave the mutation radius by default, then during the mutation, the object can only move between closely spaced containers, which dramatically reduces the efficiency of evolution.Choice of fitness function
The number of occupied containers will be a natural fitness function, but this approach is not very effective. We illustrate why.
Solution 1

Solution 2

In both solutions, three containers are occupied. But it is obvious that the second solution is preferable, since it only has one mutation left before two containers become occupied. Of course, from the first solution, as a result of a mutation, a solution may appear where only two containers are occupied, but the probability of this is much lower.
Thus, the number of occupied containers is not enough to fully assess the "fitness" of the solution. To correct the situation, we introduce an additional indicator - the sum of squares of free space in containers (a simple sum of free space in both cases will be the same).
It may happen that some of the containers are overloaded. From our point of view, such a decision is not valid and it would be possible to get rid of such members of the gene pool by giving them a rating of
null . On the other hand, congestion may be small, while the solution does not take so many containers and there is a chance that as a result of a mutation or a successful crossing, the reload will disappear.We introduce the third indicator to evaluate the solution - the sum of the squares of the overloads.
Thus, to adequately evaluate a solution, it takes three numbers. It would be possible to reduce them to some integral index, however, EvoJ allows to return any
Comparable value from the fitness function. Let's get our own class for this. public class PackRating implements Comparable { private int binsUsed; private int score; private int overflow; public PackRating(int binsUsed, int score, int overflow) { this.binsUsed = binsUsed; this.score = score; this.overflow = overflow; } public int compareTo(Object o) { PackRating other = (PackRating) o; if (this.overflow != other.overflow) { return other.overflow - this.overflow; } if (this.binsUsed != other.binsUsed) { return other.binsUsed - this.binsUsed; } return this.score - other.score; } public int getBinsUsed() { return binsUsed; } public int getOverflow() { return overflow; } public int getScore() { return score; } } Here the
binsUsed field is the number of used containers. The score field is the sum of the squares of free space in the containers. And finally, the overflow field is the sum of the squares of container overloads.The comparison procedure considers any decision without overload to be better than any solution to overload, if the overloads are equal, the occupied containers start to be taken into account (less is better), and finally, if the same number of containers are occupied, the
score field starts to be taken into account (the more - better) .It remains to implement the fitness function. To do this, as in the examples from the previous article , expanding the AbstractSimpleRating class.
public class BinPackRatingCalculator extends AbstractSimpleRating<Solution> { private int[] items; private int[] bins; public BinPackRatingCalculator(int[] items, int[] bins) { this.items = items; this.bins = bins; } @Override protected Comparable doCalcRating(Solution solution) { int[] tmpBins = new int[bins.length]; int score = 0; int overflow = 0; int binsUsed = 0; final List<Integer> indicex = solution.getBinIndices(); for (int item = 0; item < indicex.size(); item++) { Integer binIndex = indicex.get(item); tmpBins[binIndex] += items[item]; } for (int bin = 0; bin < tmpBins.length; bin++) { int dl = bins[bin] - tmpBins[bin]; final int dl2 = dl * dl; if (dl < 0) { overflow += dl2; } else { score += dl2; } if (tmpBins[bin] > 0) { binsUsed++; } } return new PackRating(binsUsed, score, overflow); } } We will not analyze this code in detail; it simply calculates our fitness indicators and returns them as an instance of the
PackRating class.Making everything work
Create a new class with the
main method: public static void main(String[] args) { int[] items = {3, 2, 4, 4, 5, 3, 4, 5, 6}; int[] bins = {8, 8, 8, 8, 8, 4, 12, 12, 8, 6}; Map<String, String> context = new HashMap<String, String>(); context.put("itemsCount", Integer.toString(items.length)); context.put("lastBinIndex", Integer.toString(bins.length - 1)); DefaultPoolFactory factory = new DefaultPoolFactory(); GenePool<Solution> pool = factory.createPool(200, Solution.class, context); DefaultHandler handler = new DefaultHandler(new BinPackRatingCalculator(items, bins), null, null, null); handler.iterate(pool, 40); Solution bestSolution = pool.getBestSolution(); showSolution(bestSolution, bins, items); } Here the
items array contains the conditional sizes of the items. The bins array is the conditional capacity of the available containers. A feature of the above code is the use of a context with variables to specify the length of the list from the Solution interface and limit the possible values. Otherwise, the code repeats what was shown in the previous article : creating a population factory, creating a population of 200 individuals, creating a handler, and performing 40 iterations.The size of the population and the number of iterations are chosen experimentally.
The code above is executed fairly quickly, and even 1000 iterations over a population of 200 solutions on my four-year laptop takes about two seconds.
Afterword
We looked at how to apply the genetic algorithm to solving one of the classic NP-complex problems. It should be noted that the genetic algorithm does not guarantee finding the best solution, but allows you to get very close to it, which in most cases is sufficient.
For those interested , the source code of the considered example is laid out in the form of a Maven project.
Thanks for attention.
Source: https://habr.com/ru/post/139646/
All Articles