Haskell - Design
They say that every programmer should write at least one compiler in his life or invent some programming language. The design of a new language is not an easy task, because you need to think through dozens of parameters that, like Lego cubes, should be well combined with each other. One unfortunate decision can erase the fate of the language, when it has not even been published yet. Hundreds of languages live in oblivion, pushed by elder brothers from the podium, but the world with a tenacity worthy of a better application gives birth to two or three new ones every year. Time will tell if they even fall into the “group of alternative worldviews”, or even become mainstream. Fortunately, my language is not necessary, because it can not be programmed - they can only admire. For this is the Haskell code visualization language, the design of which will be discussed in the article.
')
Haskell is a great language. It is very expressive and capacious. The code turns out to be an order of magnitude more compact than the code in imperative languages (C ++, Java, C #), despite the fact that it has less syntactic structures. The pure functional nature of Haskell and its design make the code look like a mathematical notation. Take for example the indicative (but not the best) version of factorial:
These two lines perfectly recognize the recurrent factorial formula familiar from school:
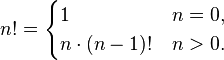
Of course, a certain recursive factorial will not be much worse in any other language, which may raise doubts, is it really Haskell expressive.
The trick is that both functions are written in a functional style, so there is not much difference between them. However, having regretted the stack, we could use a cycle in an imperative language, which already looks completely different:
Programmers are well aware that the last two examples can be visualized using a flowchart:

The second scheme, in principle, describes what happens in the Haskell recursive code. And although the flowcharts are visualization, they are still different from what I want: they show what is happening , and not what it looks like . I want to transfer the code to the three-dimensional scene, so that the scene is beautiful, intuitive and, if possible, unusual. The meaning of visualization is in this.
When designing a language, you have to think about how to expand it later. If you do wrong or inconvenient, there will be no room for new projects without destroying backward compatibility. Stories such examples are known; This cup has not passed even some very popular languages (for example, Python 3.0, which is not compatible with earlier versions). To a large extent, very small things, so to speak, syntax in small things affect the extensibility of design. With successful parts, the whole language is built as one big and well thought out designer. Haskell is one of them, which means that the visualization language should also hold a brand. And here I can not even make a discount on the fact that the design of Haskell is known - I still have to overcome these difficulties from the very beginning. Although in a sense, I, of course, easier.
So, you need to think over the design of the graphic language, rather independent, but at the same time visual and aesthetically useful. It is necessary to think over separate syntactic units, at the same time looking to a higher level - at their connection and at their meaning in the general outline. Proceeding from the very factorial, I plan to someday come up with sketches, even for such Haskell code:
Or for this:
In the meantime, I have the factorial code, and the visualization language began with it:
Here we see several syntactic constructions:
In turn, each function body is divided into a tree-like computational expression. Take the second case. Representing the elements of this tree in the form of boxes, we get the first rough version:
Immediately, the flaws appear. You can imagine how the visualization of the code will grow if you add any more actions and expressions to the function body. Why are there! Expressions can themselves consist of expressions, and simply associating each element with a box will result in us simply getting a long and non-intuitive chain of boxes. The solution "in the forehead" is not suitable here. Recall a useful fact: a clear incarnation of a tree structure is a pyramid. A computational expression can also be represented in this form, even in several ways:

The last picture is subjectively prettier due to the characteristic pyramidal protrusions. It would be possible to dwell on this form, but there is a feature among binary functions that they can be operators. The difference between the operators and the functions is purely intuitive, but from the point of view of the language it is the same thing, it is simply written differently - in the functional and infix records:
The default operators are used in the infix notation, but the functional is also valid:
And this fact can be easily displayed during visualization. In the following sketch, in addition to highlighting the infix form, I increased the final syntactic units (variables and constants) twice:
The height of the pyramid decreased, which is good, and it became clear where the infix notation was and where it was functional. This approach becomes useful when setting up consecutive calculations:
And for functions with a large number of arguments, it is worth keeping the gap between the boxes.
The sketches show that the length of the boxes depends on the name on the box and on the space occupied by the arguments. There is nothing you can do: the inscription is needed, and you should not reduce it in size, otherwise we will lose uniformity. This can be customized on a web page or in a document, and the code should look strictly, because it is easier to read. Therefore, complex, massive computational expressions will also look impressive. Let's look at the function for the Fibonacci numbers:
The expression (and it works too!) Looks very beautiful. Let's try to build a sketch for it, remembering that the “colon” sign, used twice, is written in infix form, and zipWith is a function that takes three arguments: (+), fibs and (tail fibs). The problem here appears with a plus in brackets. The sign is passed to another function as an argument, and for Haskell this is a normal and very useful phenomenon, known as the “higher order function.” In addition, the operator + has both its own arguments bitten off, and this is already called a section. According to our past rules, the + operator should be the final argument with an enlarged box. In principle, this is normal:
But looking into the future, we can reflect on how sections and curried functions will look like in general. Take for example such a little artificial code:
Here are three functions: ops returns a list of operators, func - performs an action passed as op on the x and y arguments, and inside result all this is used and something is calculated. To be honest, when executing, result will return the following list: [5, 6, -1], and it is easy to see how it turned out. The map function (func 2 3) has been applied to all operators in the ops list. In this case, we are interested in that (func 2 3) is a curried record, in which one argument remains vacant. Operators in brackets are also curried (more correctly, truncated), everything has already been stolen from us ... that is, two arguments have been selected. This is not reflected in the Haskell code, and a strange entry like this:
may not tell us anything if we don’t know what the map and null functions do, and if the type signatures are not specified. However, in the visualization we could clearly show that these functions require some more arguments. It is enough to postulate that the arguments fit into the grooves of the functions, and the number of slots corresponds to arity. Here is the result for the result and nullMap functions:
When designing computational expressions, the question of proportions still remains significant, and here a total revelry of fantasy is possible. Parameters can be element height, the distance between the arguments, the length and depth of the empty groove, the height and length of the finite elements, the size of the pyramidal indent. If you arm yourself with the knowledge of harmony, then, probably, it is worthwhile to bring the golden section in proportions. It makes everything better!
An important construction of any language is conditional transitions. In Haskell, the if statement is also there, and it is such that the else statement must accompany it. There can be no expression for which one of the alternatives is missing - in the world where everything is a function, the result should always be returned. Below is the calculation of factorial with if (we, like last time, do not think that n can come negative):
Here you can format the code in any way. then and else are not sensitive to indents and can be located on a new line (only counting at least one whitespace character from the function function):
Perhaps these permutations somehow help to come up with the design of this design. The naive hyphenation of the words if, then, and else as the lowest layers of the pyramids intersects somewhat with the previous variant and confuses. But if you separate them by some separate element, it will turn out to be more interesting. Compare the following two options:
By giving vent to fantasy, you can achieve some intuitiveness of the latter. What is an if? This is when a boolean expression is checked for truth, that is, for a match with True. Constructors, puzzles and something else are built on the coincidence principle: there is a coincidence - the pin fits the slot; no coincidence - well, sorry ... Let's try to bring this concept into the sketch:
It looks interesting and encourages to fantasize further. You can experiment with position, shape, size, but you need to remember that if-then-else is an expression, and it will be used inside other expressions. That is, since we limit ourselves in space for the sake of expressiveness, then the conditional operator should not go beyond certain empirical frameworks.
Perhaps, for if-then-else, this is not difficult, and these syntactic elements, like goodies, will fit in any part of the expression, but here's a related case-design can be a hassle. She is able to expand: the number of alternatives is unlimited. Rewrite the factorial function:
There is something to think about. A new semantics is added in the case-construction: pattern matching. Here, I confess, I have not yet come up with a decent option. But you can try by analogy with one of the latest if sketches:
The meaning of the comparison with the sample is that on each of the cubes before the sign "->" there can be a rather large expression. The possibilities are enormous: here there is a splitting of the lists, and an arbitrarily deep comparison with algebraic data types, and even — with the extension of the View Patterns language — a syntax that resembles functions. I will show only a simple, fairly typical code, where pattern matching is used inside a case:
Apparently, while there is no clarity on how to represent algebraic data types, lists, tuples, etc., the case construction will be unconvincing.
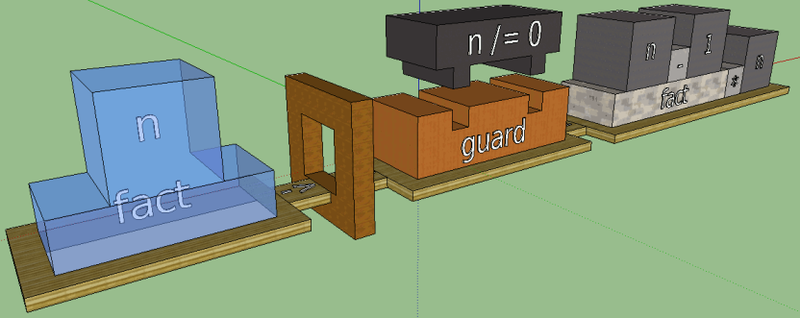
Now, nevertheless, we put aside computational expressions and try to complete the visualization of the factorial function with its name and security expressions.
About security expressions have something to say. These are ordinary expressions, but they always return a boolean value — True or False. They serve as certain filters, as if not missing execution in the body, if the condition is not true. Playing with this concept, you can come up with something like the notorious if. We estimate the following option:

A box with equality (“bridge”) emerged from the desire to combine the guard expressions and the function body in the same way as in the code. And this seems to be an interesting idea. Developing, it grew into something more - into a visual separation of parts (the name of a function; guard expressions; a computational expression). You can go further: put them on the platform, thereby outlining the space of each of the parts.
In the code, the guard expression starts with the character '|'. If it were not there, the code would look contradictory:
The compiler would not understand what the letters and symbols are after the word fact. The vertical bar is a necessary element of syntax, and therefore we need to add it to the visualization. It is logical to put something to the left of the platform with a boolean expression; it could be, for example, a “wall”:
But is it intuitive? A solid box looks like an obstacle, a prohibition, and we need a condition, a variability. If we present the progress in the form of a cube, then, moving from the name of the function to the guard expression, will simply collide with the wall - and none of the function bodies will be achieved. In this reflection lies the key to a more intuitive option: what if you make a hole in the wall? You can think of yourself this way: if the logical condition is true, the cube will pass through the hole and get where it is needed. The direction of movement should also be visualized: let the bridges with arrows show it - they will also help to connect the right and left parts of the function:

Much better! Now visualize the function name with arguments. Again, here we are dealing with pattern matching, and, in an amicable way, it would be worth combining it with arity. Cutouts for the arguments we have learned to do, they will be useful here. Without comparison with the sample, we would have this option:
So, the basis of the graphic language has been built, and we now roughly represent what it should look like. For a clear picture, you still need to deal with such important things as algebraic data types, lists, tuples, and pattern matching. When it’s done with them, ideas about what to do with type declarations, do-structures, list generators, as-samples, class types, class incarnations, and other great elements of Haskell syntax are likely to appear.
Let's start with algebraic data types, lists, and pattern matching. In the case example above, we tried to visualize the ADT and pattern matching. Imagine that arity instead of cutouts is denoted by protrusions. The picture with case, True and False will then be incorrect, because these two constructors have arity equal to zero. However, the arity of Just is 1, - and it will have one overhang.

Lists are created using the infix operator ":" (which is actually a type constructor, but this is another story [1]). We already know how to visualize it. Take a more complicated case, when there are both “unimportant” elements and an empty list. Here is a hypothetical code:
Already the constructions of the Haskell language clearly demonstrate their essence. An unimportant argument is replaced by an underscore, and an empty list with empty square brackets. We take this into account when rendering. Not visible in the formalism of the code only the differences between the arguments x1, x2 and xs from the first alternative. Meanwhile, x1 and x2 are split elements of the front list, and xs is the rest of the possible empty list. It would be useful to show the difference somehow.
Yes, the lists look very. I especially like the “unimportant” element. What about tuples? Well, there’s no need to be wise: just put each element of the tuple in the groove on the common board. It is impossible to confuse with the function, since the tuple does not have a name, and its base is thinner. For reliability, you can change the color.
Not such a difficult task was! So, logically speaking, you can build a language for visualization. It's okay if some designs will be changed beyond recognition through several versions. Now, not touching on how to visualize the type declaration, I risk then discovering that they do not fit into the semi-prepared schema. It is necessary to change something, to sacrifice something, but the general principles of visualization will remain the same. Of course, there were vast spaces for fantasy. I have not yet selected colors and shades, have not thought about fonts, and the shape of the elements can be improved in many ways. There was even such an idea: make boxes with inscriptions made of glass, and put the inscription inside, and make it all sparkle with reflected light. Perpetuate, so to speak, the code in the glass. It would probably be something like this:

Beauty, which is to say. And it already seems that the main costs here are to invent a design, and visualization can be quickly concocted in some graphic editor, but ... In reality, everything is somewhat more complicated, because a program is needed for visualization, and not a static 3D scene. This is the program that I create in the “GraphServer” project. The task is complicated by the fact that not all designs I came up with visualization; already during the writing of this article, some constructions were strongly modified or invented. But even that which is ready at the moment looks promising.
This is a cross article. On the creation of a server visualization, read the article "Haskell - Aesthetics . "
PS I apologize for not quite high-quality pictures. Habrastorage seems to be doing something with them.
[1] - Fix for the following comment: it-talk.org/post76900.html#p76900

')
Haskell is a great language. It is very expressive and capacious. The code turns out to be an order of magnitude more compact than the code in imperative languages (C ++, Java, C #), despite the fact that it has less syntactic structures. The pure functional nature of Haskell and its design make the code look like a mathematical notation. Take for example the indicative (but not the best) version of factorial:
fact n | n == 0 = 1
| n > 0 = n * fact ( n - 1 )
These two lines perfectly recognize the recurrent factorial formula familiar from school:
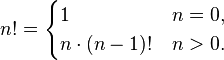
Of course, a certain recursive factorial will not be much worse in any other language, which may raise doubts, is it really Haskell expressive.
int fact ( int n )
{
if ( n == 0 ) return 1 ;
return n * fact ( n - 1 ) ;
}
The trick is that both functions are written in a functional style, so there is not much difference between them. However, having regretted the stack, we could use a cycle in an imperative language, which already looks completely different:
int fact ( int n )
{
int f = 1 ;
for ( int i = 2 ; i <= n ; ++ i )
f * = i ;
return f ;
}
Programmers are well aware that the last two examples can be visualized using a flowchart:

The second scheme, in principle, describes what happens in the Haskell recursive code. And although the flowcharts are visualization, they are still different from what I want: they show what is happening , and not what it looks like . I want to transfer the code to the three-dimensional scene, so that the scene is beautiful, intuitive and, if possible, unusual. The meaning of visualization is in this.
When designing a language, you have to think about how to expand it later. If you do wrong or inconvenient, there will be no room for new projects without destroying backward compatibility. Stories such examples are known; This cup has not passed even some very popular languages (for example, Python 3.0, which is not compatible with earlier versions). To a large extent, very small things, so to speak, syntax in small things affect the extensibility of design. With successful parts, the whole language is built as one big and well thought out designer. Haskell is one of them, which means that the visualization language should also hold a brand. And here I can not even make a discount on the fact that the design of Haskell is known - I still have to overcome these difficulties from the very beginning. Although in a sense, I, of course, easier.
So, you need to think over the design of the graphic language, rather independent, but at the same time visual and aesthetically useful. It is necessary to think over separate syntactic units, at the same time looking to a higher level - at their connection and at their meaning in the general outline. Proceeding from the very factorial, I plan to someday come up with sketches, even for such Haskell code:
- | | Box side drawings.
- | | It should be used only in this module.
f :: PreparedTextureObjects
-> GLfVertex3
-> ( BoxSide , QuadColorSpec )
-> ( [ BoxSide ] , [ IO ( ) ] )
-> ( [ BoxSide ] , [ IO ( ) ] )
f texRes boxDim ( side , qColorSpec ) ( sList , ioList ) = let
boxIO = do setQuadColorSpec texRes qColorSpec
GL . renderPrimitive GL . Quads ( boxSide boxDim side )
in ( side: sList , boxIO: ioList )
Or for this:
data QuadColorSpec = QuadTexture TextureName
| QuadPlainColor GLfColor4
| NoQuadColorSpec
deriving ( Show )
data ObjectTextureSpec = BoxTextureSpec
{ quadSideTexes :: [ ( BoxSide , QuadColorSpec ) ]
, defQuadSideTex :: QuadColorSpec
} deriving ( Show )
data CornerCoord = UR | DR | DL | UL
deriving ( Show )
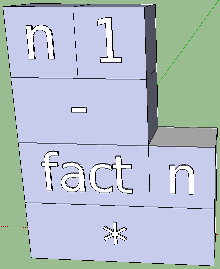
In the meantime, I have the factorial code, and the visualization language began with it:
fact n | n == 0 = 1
| n / = 0 = fact ( n - 1 ) * n
Here we see several syntactic constructions:
| function name | fact | |
| Argument | n | |
| 2 security expressions | | n == 0 | |
| | n / = 0 | ||
| 2 function bodies | = 1 | |
| = fact (n - 1) * n |
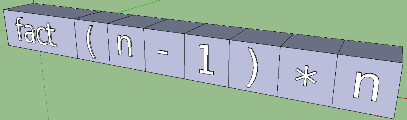
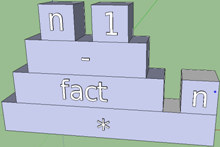
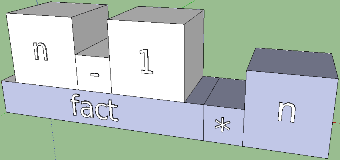
In turn, each function body is divided into a tree-like computational expression. Take the second case. Representing the elements of this tree in the form of boxes, we get the first rough version:

Immediately, the flaws appear. You can imagine how the visualization of the code will grow if you add any more actions and expressions to the function body. Why are there! Expressions can themselves consist of expressions, and simply associating each element with a box will result in us simply getting a long and non-intuitive chain of boxes. The solution "in the forehead" is not suitable here. Recall a useful fact: a clear incarnation of a tree structure is a pyramid. A computational expression can also be represented in this form, even in several ways:



The last picture is subjectively prettier due to the characteristic pyramidal protrusions. It would be possible to dwell on this form, but there is a feature among binary functions that they can be operators. The difference between the operators and the functions is purely intuitive, but from the point of view of the language it is the same thing, it is simply written differently - in the functional and infix records:
isListElement x xs = elem x xs - functional form
isListElement 'x xs = x ` elem` xs - infix form
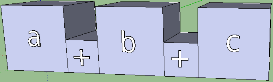
The default operators are used in the infix notation, but the functional is also valid:
add a b = a + b
add 'a b = ( + ) a b
And this fact can be easily displayed during visualization. In the following sketch, in addition to highlighting the infix form, I increased the final syntactic units (variables and constants) twice:

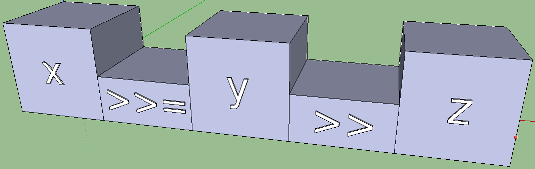
The height of the pyramid decreased, which is good, and it became clear where the infix notation was and where it was functional. This approach becomes useful when setting up consecutive calculations:
add3 a b c = a + b + c
someF x y z = x >> = y >> z


And for functions with a large number of arguments, it is worth keeping the gap between the boxes.
The sketches show that the length of the boxes depends on the name on the box and on the space occupied by the arguments. There is nothing you can do: the inscription is needed, and you should not reduce it in size, otherwise we will lose uniformity. This can be customized on a web page or in a document, and the code should look strictly, because it is easier to read. Therefore, complex, massive computational expressions will also look impressive. Let's look at the function for the Fibonacci numbers:
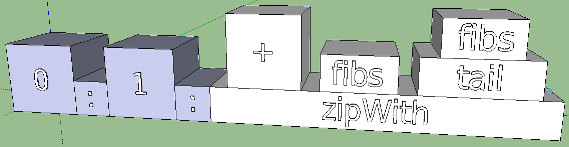
fibs = 0 : 1 : zipWith ( + ) fibs ( tail fibs )
The expression (and it works too!) Looks very beautiful. Let's try to build a sketch for it, remembering that the “colon” sign, used twice, is written in infix form, and zipWith is a function that takes three arguments: (+), fibs and (tail fibs). The problem here appears with a plus in brackets. The sign is passed to another function as an argument, and for Haskell this is a normal and very useful phenomenon, known as the “higher order function.” In addition, the operator + has both its own arguments bitten off, and this is already called a section. According to our past rules, the + operator should be the final argument with an enlarged box. In principle, this is normal:

But looking into the future, we can reflect on how sections and curried functions will look like in general. Take for example such a little artificial code:
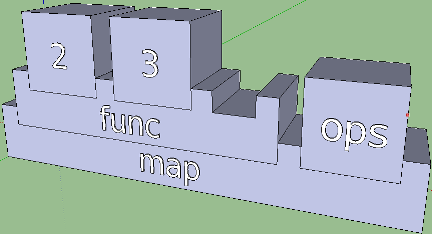
ops = [ ( + ) , ( * ) , ( - ) ]
func x y op = x `op` y
result = map ( func 2 3 ) ops
Here are three functions: ops returns a list of operators, func - performs an action passed as op on the x and y arguments, and inside result all this is used and something is calculated. To be honest, when executing, result will return the following list: [5, 6, -1], and it is easy to see how it turned out. The map function (func 2 3) has been applied to all operators in the ops list. In this case, we are interested in that (func 2 3) is a curried record, in which one argument remains vacant. Operators in brackets are also curried (more correctly, truncated), everything has already been stolen from us ... that is, two arguments have been selected. This is not reflected in the Haskell code, and a strange entry like this:
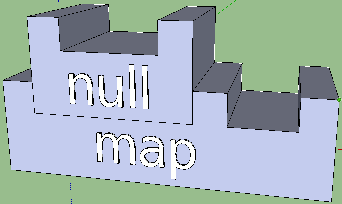
nullMap = map null
may not tell us anything if we don’t know what the map and null functions do, and if the type signatures are not specified. However, in the visualization we could clearly show that these functions require some more arguments. It is enough to postulate that the arguments fit into the grooves of the functions, and the number of slots corresponds to arity. Here is the result for the result and nullMap functions:


When designing computational expressions, the question of proportions still remains significant, and here a total revelry of fantasy is possible. Parameters can be element height, the distance between the arguments, the length and depth of the empty groove, the height and length of the finite elements, the size of the pyramidal indent. If you arm yourself with the knowledge of harmony, then, probably, it is worthwhile to bring the golden section in proportions. It makes everything better!
An important construction of any language is conditional transitions. In Haskell, the if statement is also there, and it is such that the else statement must accompany it. There can be no expression for which one of the alternatives is missing - in the world where everything is a function, the result should always be returned. Below is the calculation of factorial with if (we, like last time, do not think that n can come negative):
fact n = if n == 0 then 1 else fact ( n - 1 ) * n
Here you can format the code in any way. then and else are not sensitive to indents and can be located on a new line (only counting at least one whitespace character from the function function):
fact n = if n == 0
then 1
else fact ( n - 1 ) * n
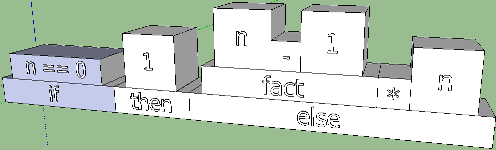
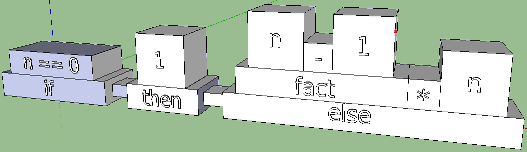
Perhaps these permutations somehow help to come up with the design of this design. The naive hyphenation of the words if, then, and else as the lowest layers of the pyramids intersects somewhat with the previous variant and confuses. But if you separate them by some separate element, it will turn out to be more interesting. Compare the following two options:


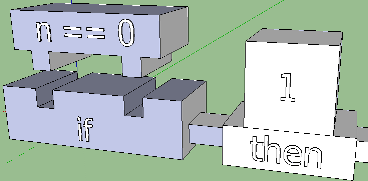
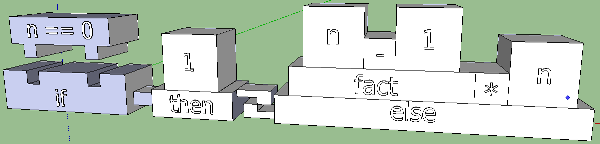
By giving vent to fantasy, you can achieve some intuitiveness of the latter. What is an if? This is when a boolean expression is checked for truth, that is, for a match with True. Constructors, puzzles and something else are built on the coincidence principle: there is a coincidence - the pin fits the slot; no coincidence - well, sorry ... Let's try to bring this concept into the sketch:


It looks interesting and encourages to fantasize further. You can experiment with position, shape, size, but you need to remember that if-then-else is an expression, and it will be used inside other expressions. That is, since we limit ourselves in space for the sake of expressiveness, then the conditional operator should not go beyond certain empirical frameworks.
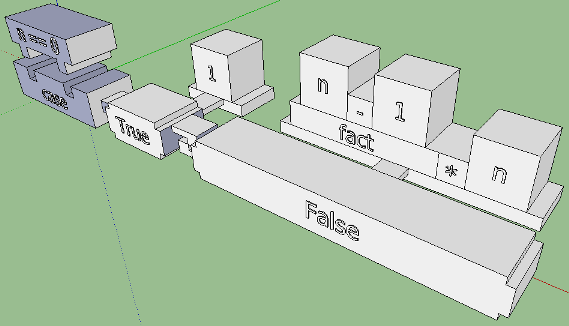
Perhaps, for if-then-else, this is not difficult, and these syntactic elements, like goodies, will fit in any part of the expression, but here's a related case-design can be a hassle. She is able to expand: the number of alternatives is unlimited. Rewrite the factorial function:
fact n = case n == 0 of
True -> 1
False -> fact ( n - 1 ) * n
There is something to think about. A new semantics is added in the case-construction: pattern matching. Here, I confess, I have not yet come up with a decent option. But you can try by analogy with one of the latest if sketches:

The meaning of the comparison with the sample is that on each of the cubes before the sign "->" there can be a rather large expression. The possibilities are enormous: here there is a splitting of the lists, and an arbitrarily deep comparison with algebraic data types, and even — with the extension of the View Patterns language — a syntax that resembles functions. I will show only a simple, fairly typical code, where pattern matching is used inside a case:
toHabrFormat ( s , ( ch: [ ] ) ) = s ++ [ ch ]
toHabrFormat a @ ( s , b @ ( ch: inStr ) ) = let formatted = ( foldr1 ( <|> ) formatters ) a
in case formatted of
Just ( res , [ ] ) -> res
Just ( res , ( r: rs ) ) -> toHabrFormat ( res ++ [ r ] , rs )
Nothing -> toHabrFormat ( s ++ [ ch ] , inStr )
Apparently, while there is no clarity on how to represent algebraic data types, lists, tuples, etc., the case construction will be unconvincing.
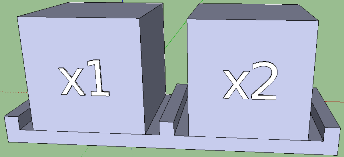
Now, nevertheless, we put aside computational expressions and try to complete the visualization of the factorial function with its name and security expressions.
fact n | n == 0 = 1
| n / = 0 = fact ( n - 1 ) * n
About security expressions have something to say. These are ordinary expressions, but they always return a boolean value — True or False. They serve as certain filters, as if not missing execution in the body, if the condition is not true. Playing with this concept, you can come up with something like the notorious if. We estimate the following option:

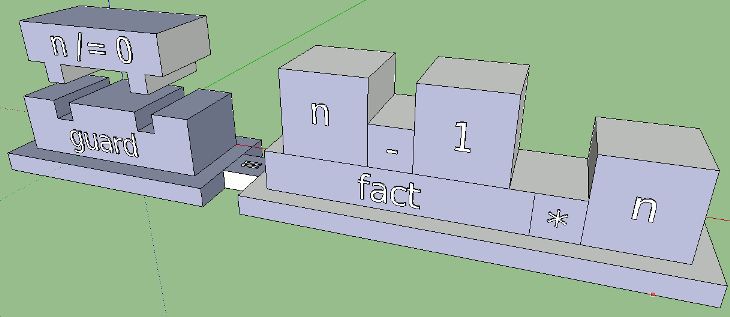
A box with equality (“bridge”) emerged from the desire to combine the guard expressions and the function body in the same way as in the code. And this seems to be an interesting idea. Developing, it grew into something more - into a visual separation of parts (the name of a function; guard expressions; a computational expression). You can go further: put them on the platform, thereby outlining the space of each of the parts.

In the code, the guard expression starts with the character '|'. If it were not there, the code would look contradictory:
fact n n == 0 = 1
n / = 0 = fact ( n - 1 ) * n
The compiler would not understand what the letters and symbols are after the word fact. The vertical bar is a necessary element of syntax, and therefore we need to add it to the visualization. It is logical to put something to the left of the platform with a boolean expression; it could be, for example, a “wall”:

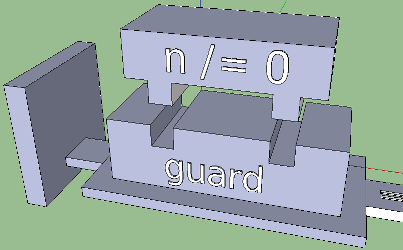
But is it intuitive? A solid box looks like an obstacle, a prohibition, and we need a condition, a variability. If we present the progress in the form of a cube, then, moving from the name of the function to the guard expression, will simply collide with the wall - and none of the function bodies will be achieved. In this reflection lies the key to a more intuitive option: what if you make a hole in the wall? You can think of yourself this way: if the logical condition is true, the cube will pass through the hole and get where it is needed. The direction of movement should also be visualized: let the bridges with arrows show it - they will also help to connect the right and left parts of the function:

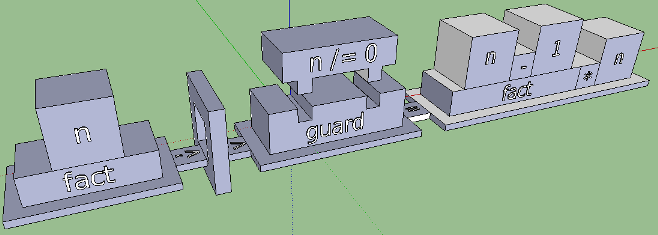
Much better! Now visualize the function name with arguments. Again, here we are dealing with pattern matching, and, in an amicable way, it would be worth combining it with arity. Cutouts for the arguments we have learned to do, they will be useful here. Without comparison with the sample, we would have this option:

So, the basis of the graphic language has been built, and we now roughly represent what it should look like. For a clear picture, you still need to deal with such important things as algebraic data types, lists, tuples, and pattern matching. When it’s done with them, ideas about what to do with type declarations, do-structures, list generators, as-samples, class types, class incarnations, and other great elements of Haskell syntax are likely to appear.
Let's start with algebraic data types, lists, and pattern matching. In the case example above, we tried to visualize the ADT and pattern matching. Imagine that arity instead of cutouts is denoted by protrusions. The picture with case, True and False will then be incorrect, because these two constructors have arity equal to zero. However, the arity of Just is 1, - and it will have one overhang.

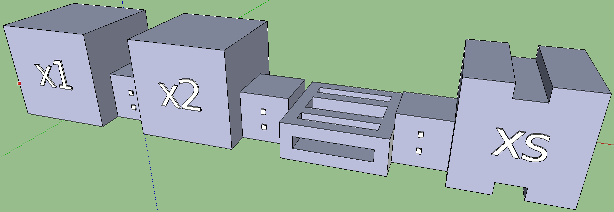
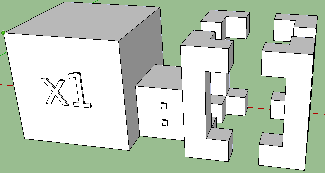
Lists are created using the infix operator ":" (which is actually a type constructor, but this is another story [1]). We already know how to visualize it. Take a more complicated case, when there are both “unimportant” elements and an empty list. Here is a hypothetical code:
someFunc someList = case someList of
( x1: x2: _ : xs ) -> Just ( x1 , x2 )
( x1: [ ] ) -> Just ( x1 , x1 )
[ ] -> Nothing
Already the constructions of the Haskell language clearly demonstrate their essence. An unimportant argument is replaced by an underscore, and an empty list with empty square brackets. We take this into account when rendering. Not visible in the formalism of the code only the differences between the arguments x1, x2 and xs from the first alternative. Meanwhile, x1 and x2 are split elements of the front list, and xs is the rest of the possible empty list. It would be useful to show the difference somehow.


Yes, the lists look very. I especially like the “unimportant” element. What about tuples? Well, there’s no need to be wise: just put each element of the tuple in the groove on the common board. It is impossible to confuse with the function, since the tuple does not have a name, and its base is thinner. For reliability, you can change the color.

Not such a difficult task was! So, logically speaking, you can build a language for visualization. It's okay if some designs will be changed beyond recognition through several versions. Now, not touching on how to visualize the type declaration, I risk then discovering that they do not fit into the semi-prepared schema. It is necessary to change something, to sacrifice something, but the general principles of visualization will remain the same. Of course, there were vast spaces for fantasy. I have not yet selected colors and shades, have not thought about fonts, and the shape of the elements can be improved in many ways. There was even such an idea: make boxes with inscriptions made of glass, and put the inscription inside, and make it all sparkle with reflected light. Perpetuate, so to speak, the code in the glass. It would probably be something like this:

Beauty, which is to say. And it already seems that the main costs here are to invent a design, and visualization can be quickly concocted in some graphic editor, but ... In reality, everything is somewhat more complicated, because a program is needed for visualization, and not a static 3D scene. This is the program that I create in the “GraphServer” project. The task is complicated by the fact that not all designs I came up with visualization; already during the writing of this article, some constructions were strongly modified or invented. But even that which is ready at the moment looks promising.
This is a cross article. On the creation of a server visualization, read the article "Haskell - Aesthetics . "
PS I apologize for not quite high-quality pictures. Habrastorage seems to be doing something with them.
[1] - Fix for the following comment: it-talk.org/post76900.html#p76900
Source: https://habr.com/ru/post/139167/
All Articles