Sqrt-decomposition (root optimization)
Sqrt decomposition is a method or data structure that allows for online operations such as calculating the amount on a segment for  and update item for
and update item for  . There are more efficient structures, such as a fenwick tree or a segment tree , which both requests process for
. There are more efficient structures, such as a fenwick tree or a segment tree , which both requests process for 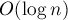 . However, I want to tell you about root optimization, because This method has an idea applicable to other types of tasks.
. However, I want to tell you about root optimization, because This method has an idea applicable to other types of tasks.
Let us be given an array A [i], which receives requests of the form:
We can predict an array of partial sums, namely: . However, a change request will require recalculation of partial sums (containing this element) and in the worst case will be asymptotic of order
. However, a change request will require recalculation of partial sums (containing this element) and in the worst case will be asymptotic of order 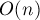 that is not good.
that is not good.
The main idea is that *
*  =
=  . Namely, if we have
. Namely, if we have  elements, then we can break them all into
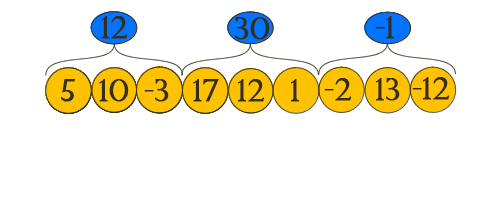
elements, then we can break them all into  blocks where each is long
blocks where each is long  except maybe the last one. Then, for all blocks, we calculate the sum of the numbers on it, you can immediately see that the auxiliary array will occupy
except maybe the last one. Then, for all blocks, we calculate the sum of the numbers on it, you can immediately see that the auxiliary array will occupy  of memory.
of memory.
We describe the construction of the sqrtSums [] array:
')
Consider the sum request [L; R], for a “quick” answer to it, it is necessary to make the most of the information already available. As we have said, Sum [L; R] = Sum [0, R] - Sum [0; L-1]. It remains to learn how to handle the request Sum [0; R]. Note that the first few segments , as the segments of all
, as the segments of all  ). However, we will have a “tail” of the form:
). However, we will have a “tail” of the form:  will not affect). Here is an example implementation:
will not affect). Here is an example implementation:
In many structures, to implement this query, you need to go down the tree, or count the hash function, or something else ... However, here we need to change only 2 values (each element is included in exactly one "sqrt-segment")
To answer RMQ (Range Min / Max Query) queries, you need almost the same thing as for amounts. However, it is worth noting that in order to update the “stupid” item, we will need time (when updating an element, recalculate min / max on the entire “sqrt-segment”), but if we impose some restrictions on the updates, we will achieve an estimate
time (when updating an element, recalculate min / max on the entire “sqrt-segment”), but if we impose some restrictions on the updates, we will achieve an estimate  . Namely, when solving the problem of finding a minimum / maximum, allow only reduce / increase the element.
. Namely, when solving the problem of finding a minimum / maximum, allow only reduce / increase the element.
Code to update the minimum:
Similarly, to update the maximum:
It is necessary to add that in the task RMQ, the task is not reduced to [0; R] - [0; L-1], i.e. it is necessary to calculate the minimum / maximum from L to R (not counting again, the “sqrt-segments” that are fully included in [L; R], think about why the asymptotics will not change, and the net operating time may even improve ...).
To calculate the GCD (Greatest Common Divisor), we will not be able to use the "chip" that we cranked for min / max. Therefore, both operations are calculated for .
.
The code for GCD (for the minimum and maximum, the getGCD functions will be replaced by min / max):
Used this site, namely .
Since the article was inspired by a lecture from the Kharkov Winter Computer School, I will throw the site , perhaps soon there will be a collection for this year, with video lectures.
So far everything, I hope that was understandable.
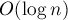 . However, I want to tell you about root optimization, because This method has an idea applicable to other types of tasks.
. However, I want to tell you about root optimization, because This method has an idea applicable to other types of tasks.
Formulation of the problem
Let us be given an array A [i], which receives requests of the form:
- calculate the amount on the segment [L; R] (later, we will understand that it is similarly possible to calculate the functions min, max, gcd, etc.
- add to element A [i], delta
Naive implementation
We can predict an array of partial sums, namely:
for(int j = 0; j < i; j++) B[j] += A[i]; 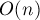 that is not good.
that is not good. Building decomposition
The main idea is that
We describe the construction of the sqrtSums [] array:
int len = (int)sqrt(n) + 1; // "sqrt-" int sqrtSums[MAXN], st = 0; // for(int i = 0; i < n; i++) sqrtSums[i / len] += A[i]; ')
Request Description
Request Amount (RSQ)
Consider the sum request [L; R], for a “quick” answer to it, it is necessary to make the most of the information already available. As we have said, Sum [L; R] = Sum [0, R] - Sum [0; L-1]. It remains to learn how to handle the request Sum [0; R]. Note that the first few segments
([0; len-1], [len; 2*len-1], ...) will be fully included in the query [0; R], which means we can use information from sqrtSums[] (for [k*len; k*len + delta] [k*len; k*len + delta] (delta <len, because otherwise we can include another segment [k*len; (k+1)*len-1] ), we can calculate it manually (delta <len, on asymptotics, int getPartSum(int r) { int it = 0, res = 0; while((it+1) * len -1 <= r) res += sqrtSums[it++]; // , for(int i = it*len; i <=r; i++) res += A[i]; // "" return res; } int getSum(int l, int r) { if(l == 0) return getPartSum(r); else return getPartSum(r) - getPartSum(l-1); } Item Change Request
In many structures, to implement this query, you need to go down the tree, or count the hash function, or something else ... However, here we need to change only 2 values (each element is included in exactly one "sqrt-segment")
int incElement(int index, int delta) { A[index] += delta; sqrtSums[index/len] += delta; } Range Min / Max / Gcd Query
To answer RMQ (Range Min / Max Query) queries, you need almost the same thing as for amounts. However, it is worth noting that in order to update the “stupid” item, we will need
Code to update the minimum:
int decElement(int index, unsigned int delta) //delta - { A[index] -= delta; sqrtSums[index/len] = min(sqrtSums[index/len], A[index]); } Similarly, to update the maximum:
int incElement(int index, unsigned int delta) //delta - { A[index] += delta; sqrtSums[index/len] = max(sqrtSums[index/len], A[index]); } It is necessary to add that in the task RMQ, the task is not reduced to [0; R] - [0; L-1], i.e. it is necessary to calculate the minimum / maximum from L to R (not counting again, the “sqrt-segments” that are fully included in [L; R], think about why the asymptotics will not change, and the net operating time may even improve ...).
To calculate the GCD (Greatest Common Divisor), we will not be able to use the "chip" that we cranked for min / max. Therefore, both operations are calculated for
The code for GCD (for the minimum and maximum, the getGCD functions will be replaced by min / max):
int getGCD(int a, int b) { while(a && b) { if(a < b) b %= a; else a %= b; } return a + b; } int gcdRQ(int l, int r) { int cur_gcd = A[l++]; for(int i = l; i <= r;) if (i % len == 0 && i + len - 1 <= r) { cur_gcd = getGCD(cur_gcd, b[i / len]); i += len; // "sqrt-" } else cur_gcd = getGCD(cur_gcd, A[i++]); } Sources
Used this site, namely .
Since the article was inspired by a lecture from the Kharkov Winter Computer School, I will throw the site , perhaps soon there will be a collection for this year, with video lectures.
So far everything, I hope that was understandable.
Source: https://habr.com/ru/post/138946/
All Articles