Introduction to the theory of interacting sequential processes (Communicating Sequential Processes - CSP)

• Part 1
• Part 2

Foreword

This text is a translation and an abbreviated retelling of the initial chapters of the book by Charles E. Hoare . The goal is to familiarize the Russian-speaking audience with this algebra of calculus of processes, which has found quite wide application in modern computational science due to the large spread of parallel systems. The closest and most understandable practical applications of CSP, I think, will be the following programming languages:

• Erlang
• Go
• Limbo

CSP is a formal mathematical language that allows to describe the interaction of parallel systems, its main application is the formal specification of parallel operation of systems, such as Transputer , in addition, it is used in the development of highly reliable e-commerce sites.
This article will explain the basics of this algebra, without which further study is impossible, basically this is a basic description of the process that covers the first half of the first chapter of the book.

Introduction

Forget temporarily everything you know about computers and programming, instead think about objects around us that can interact with us or with each other according to certain patterns of behavior. Imagine a watch, a phone or a candy dispenser. Let us take, for example, the last object, in order to describe it, we will determine the actions of the automaton that are of interest to us, and give them our names. Then for a simple vending machine selling chocolate for a coin there will be two actions:

• coin - lowering the coin into the coin receiver
• choc - getting chocolate

In the case of a more complex machine selling two chocolates: a small one (for a ruble) and a large one (for two), we get the following actions:

• in1p - lowering one ruble
• in2p - lowering two rubles
• small - getting a little chocolate
• large - getting a big chocolate bar
• out1p - getting one ruble surrender

The set of event names that interest us in this description of an object is called the alphabet . The alphabet is an immutable and predefined property of the object. It is logically impossible for an object to perform an action outside its alphabet, how impossible it is that a chocolate car would suddenly give us a radio-controlled tank. But at the same time, a machine designed for selling chocolates may not sell a single chocolate bar, for example, because it broke down or simply because no one wants chocolate bars, but despite this event, choc will remain in the alphabet of the machine, even if it never will not happen.

When choosing the alphabet, we intentionally simplify the situation and consciously ignore the properties and actions of the object that are of little interest to us. For example, the weight, color and shape of the chocolate bar are not described, as well as unconditionally important moments of her life, such as stocking chocolates, because during the work of this car all this will not especially worry the final buyer.

Every event is atomic, i.e. happens instantly. To describe the event lasting in time, a couple of events are used: initial and final. In the interval between them, other events may also occur, which means that events proceeding in time may overlap.
')
Another detail is the deliberate distraction from the exact time of execution, which simplifies the description and allows you to apply the theory regardless of the computing speed of the system. In cases where execution time is critical, this issue should be considered separately from the logical correctness of the system design.

The consequence of ignoring the temporary issue is that we refuse to consider the simultaneity of events. In cases where this is important (for example, synchronization), we present these events as one.

When choosing the alphabet, we do not need to separate the events occurring by impact from outside ( coin ) and events produced by the object itself ( choc ).

We introduce the term “ process ” to describe the behavior of a certain object, which can be described from the position of a limited number of events from the alphabet of the object. We will further adhere to the following agreement:

1. Words that begin with a small letter indicate individual events, for example: coin , choc , in2p , out1p , as well as individual letters a , b , c , etc.
2. Upper-case words denote processes, for example:
   
   • VMS is a simple trading machine.
   • VMC - more complex trading machine
   besides, the letters P , Q , R (used in the laws) denote certain arbitrary processes
   
3. The letters x , y , z are variable denoting an event.
4. The letters A , B , C denote a multitude of events.
5. The letters X , Y are process variables.
6. The alphabet of the process P is denoted as αP (alpha P), for example:
   
   • αVMS = { coin , choc }
   • αVMC = { in1p , in2p , small , large , out1p }

The process with the alphabet A , which never participates in any of the events in A, is designated as STOP _A.

Prefix

Let x be an event, and P is a process, then:

( x → P ) (pronounced “x then P”)

describes the object that first makes the event x , and then behaves like P. By definition, the process P has the same alphabet as y ( x → P ), of course, this record can only be used if x belongs to this alphabet, which can be written formally as:

α ( x → P ) = α P subject to x ∈ α P

Examples:

1. A simple trading machine breaking after giving one chocolate bar:
   

   (coin → STOP _αVMS )

2. A simple trading machine that breaks down after servicing two people:
   

   (coin → (choc → (coin → (choc → STOP _αVMS ))))

   At the very beginning, the machine can accept a coin, but can not give back the chocolate, but after the coin is inserted the machine will no longer accept the coin until the chocolate is removed.
3. The pointer can move through the maze only up and to the right in white cells:
   

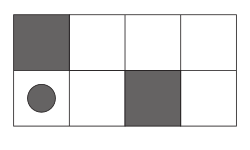
   αCTR = {up, right}
   CTR = (right → up → right → right → STOP _αCTR )

In the third example, we simplified the recording by lowering the parentheses by accepting the agreement that → is associative on the right.

Note that the following entries are not syntactically correct:

P → Q
x → y

→ must necessarily take the event to the left. The string of prefixes must end with a process. An example of a valid record would be equivalent records:

x → (y → STOP)
x → y → STOP

Thus, we clearly distinguish between an event and a process involved in one or many events.

Recursion

The prefix entry allows us to describe the behavior of the final process, but in the case of a vending machine it will be tedious to describe his whole life with its hundreds and thousands of sales. Thus, we need a way to describe repetitive actions, which will give us an opportunity to describe infinitely living processes.

Consider the usual ticking clock, considering that we will be interested only in his tics, then:

αCLOCK = {tick}

After the clock is ticked, it will remain the same clock, then we can say that the object after the tick becomes a clock is a clock:

CLOCK = (tick → CLOCK)

Making the substitution CLOCK in the right part we will receive:

  CLOCK
     = (tick → CLOCK) [original equation]
     = (tick → (tick → CLOCK)) [one permutation]
     = (tick → (tick → (tick → CLOCK))) [two substitutions] 

Thus, the behavior of a clock can be described as an infinite number of repeating ticks:

tick → tick → tick → · · ·

This way of reference to yourself will work only if the expression on the right side of the equation starts with a prefix, for example, the equation:

X = x

Nothing really determines, because it corresponds to any process. We will further call the process description starting with the prefix “protected”. Thus, if F (X) is a protected expression containing the name of the process X and αX = A, then the equation:

X = F (X)

It has the only solution with the alphabet A. It is often convenient to write this equation as:

μX: A • F (X)

where X is a local variable that can be changed:

μX: A • F (X) = μY: A • F (Y)

the equivalence of these expressions follows from the fact that the equations:

X = F (X)
Y = F (Y)

have the same solutions.

In the future, we will use both ways of defining the process: through the equation and through μ. In the second case, we will often omit the mention of the alphabet A, since it will be obvious from the context.

Examples:

1. Endless hours:
   

   CLOCK = μX: {tick} • (tick → X)

2. Vending machine selling an infinite amount of chocolates:
   

   VMS = μX: (coin → (choc → X))

   As mentioned above, this entry is a shortened version of a more formal entry:
   

   VMS = μX: {coin, choc} • (coin → (choc → X))

3. The machine exchanging five-ruble coins:
   

   αCH5A = {in5p, out2p, out1p}
   CH5A = (in5p → out2p → out1p → out2p → CH5A)

4. Another variant of the changing machine with the same alphabet:
   

   CH5A = (in5p → out1p → out1p → out1p → out2p → CH5A)

The statement that the protected expression has a solution and it is possible to uniquely show on fingers through the substitution method, substituting the process into the expression, we extend it, which can continue indefinitely, so we can write an arbitrarily long (but finite) description of the process, and if two process for an arbitrarily long time behave the same way, then we say that they are the same. A more formal proof is impossible without the exact mathematical definition given in the following chapters of the book.

Conclusion

This article did not even cover the first chapter of the book, but I hope I gave a rough understanding of what CSP is and what language it uses. Later in the first chapter, a choice is introduced (to describe branching), indirect recursion (to describe more complex processes). The basic laws of algebra of processes are proved on the basis of this primitive apparatus. The second half of the first chapter is devoted to the traces of the processes (recording the actions of the produced processes) and operations related to them.