Exact calculation of geometric predicates
Good day to you, colleagues. I suggest you read an article about the basic aspect of computational geometry - the exact calculation of predicates.
It is possible that many of you have come across the “strange” behavior of implementations of the algorithm of the vychgeoma: crashes and incorrect results. In general, there is nothing surprising in these oddities - these are the costs of transferring continuous geometry to the harsh discrete realities of floating point arithmetic. I would venture to suggest that some of you, by debugging your algorithms, solved similar problems by selecting magical constants. Most likely, if this method and led to the result, it is likely to temporary.
In this article, I will explain how to get rid of the flaws in floating-point calculations with little or no damage to efficiency. Article layout:
So, if you want to know why computational geometry is not a "science of selecting epsilons" and how to correctly and efficiently implement a geometric algorithm, click here.
')
In general, any algorithm, as a discrete structure, is implemented strictly. Problems arise in conditional blocks where the value of a predicate is checked (for example, if a point lies inside a triangle, if a segment intersects a quadrilateral, etc.).
Consider, for example, a turn, the simplest geometric predicate. This input predicate takes three points on the plane.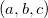 and returns 1 if c lies to the left of the directed segment ab ; -1 if on the right; and 0, if three points lie on one straight line. The predicate is implemented using the vector product:
and returns 1 if c lies to the left of the directed segment ab ; -1 if on the right; and 0, if three points lie on one straight line. The predicate is implemented using the vector product:
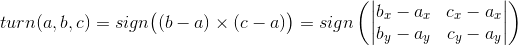
This predicate, despite its simplicity, is very important: it can be used to check, for example, if a pair of segments intersect, if a point lies inside a triangle, etc. Consider its implementation:
Consider a call to the turn function with the following input:
Despite the fact that all points lie on one straight line, the result, due to the limited accuracy of floating-point arithmetic, is not equal to collinear. Often, as a hot fix, it is believed that the vector product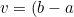\times(c - a)) can be considered zero if
can be considered zero if  less than some predefined constant e :
less than some predefined constant e :
The thought is unsuccessful, since the predicate will be incompatible at four points: for any such constant e, you can choose four points so that the predicate will return contradictory results. For example, consider two parallel, not lying on one straight line segment ab and cd (see figure).

In this figure, the triangles and
and 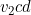 have the same area equal to e / 2 . Since the doubled area of a triangle is equal to the product of height and base, all points of a long segment ab form, on the basis of cd, triangles of the same area. This area will be less than the areas of similarly constructed triangles based on ab and vertices on cd . From this it follows, for example, that for a certain constant e, the segment ab will be collinear to the segment cd , but cd will not be collinear to the segment ab .
have the same area equal to e / 2 . Since the doubled area of a triangle is equal to the product of height and base, all points of a long segment ab form, on the basis of cd, triangles of the same area. This area will be less than the areas of similarly constructed triangles based on ab and vertices on cd . From this it follows, for example, that for a certain constant e, the segment ab will be collinear to the segment cd , but cd will not be collinear to the segment ab .
But note that usually collinear is a rather rare result. If we could produce most of the left and right turns, comparing the vector product with some constant, and counting the rest of the answers in some less effective but accurate way (for example, using long arithmetic), then we could consider our task accomplished, since on average the calculation time of the rotation would increase slightly. The calculation of the constant e, I will give in the appendix below, for those who are not afraid of tedious, but trivial calculations. After the changes, the predicate will look like this:
In general, we have already obtained an absolutely correct and fairly fast predicate. There are two subtleties: firstly, it can be accelerated a little more, and, secondly, the derivation of the formula for the constant e in the general case is quite difficult, despite significant help from symbolic arithmetic (sympy, sage, etc.) .). Now is the time to think about interval arithmetic.
The main idea of interval arithmetic is to fix a real number in a certain segment with floating-point boundaries. Any number that is exactly representable in floating arithmetic will be represented by a degenerate segment - a point.
When two intervals are added, their boundaries are added: the upper boundaries are rounded up (k plus infinity), and the lower ones are rounded down (minus infinity). It is easy to determine the remaining arithmetic operations from the following considerations: the exact value of a real number is unknown, it can be any in the segment. Hence, the resulting segment must contain the results of the arithmetic action on all pairs of numbers from the operand segments.
There are several implementations of interval arithmetic, for example, boost / interval.
Using interval arithmetic, one can much more accurately determine the “confidence interval” of the predicate calculation in floating point arithmetic. Interval arithmetic is, for obvious reasons, two to five times slower than ordinary arithmetic, but about three or four times faster than long arithmetic. So in the implementation of predicates, it makes sense to specify the confidence interval after ordinary floating point arithmetic before calling long arithmetic:
Please note that if you remove the usual arithmetic before the interval, the calculation speed will fall two to five times, but not by three or four orders of magnitude, as if we had left only long arithmetic. Sometimes it is much more difficult to estimate the predicate's confidence interval than in this case, and the performance of long arithmetic does not allow it to be used as the main means of calculation. In this case, interval arithmetic will be a reasonable compromise.
In general, long arithmetic is not the only way to accurately determine the sign of an arithmetic expression. There are several algorithms that are more efficient than long arithmetic by an order and a half. We are talking about algorithms ESSA and Adaptive Precision Arithmetic. I will not give these algorithms here, since it is easy to find detailed descriptions on the Internet. I will only make a remark that can save some time during debugging: often the coprocessor flags are set in such a way that the calculations are carried out in ten-byte real numbers, which are pushed out to eight or four-byte real numbers when assigned. Due to this, greater accuracy of computations is achieved, but this negatively affects the mentioned ESSA and Adaptive Precision Arithmetic algorithms. As for the rest, these algorithms are quite portable and quite simply realizable.
In this article, I introduced you to the method of filtered predicate calculation. In the first step of the filter (floating point arithmetic), most of the input data is effectively eliminated. In the second step (interval arithmetic), a significant part of the input data that passed the first filter is eliminated. In the third step (long arithmetic, ESSA or Adaptive Precision), the remaining data that has passed through the previous steps is processed. In our tests (a uniform distribution in the square) of their one hundred million input data, approximately two hundred thousand passed on interval arithmetic. Only a few inputs have reached the length of arithmetic, which makes it possible to make an optimistic conclusion about the effectiveness and simplicity of this approach. This approach is generally accepted: it is used, for example, by the library of computational geometry CGAL. In your tasks, you can easily use your own filters, in accordance with the nature of your input data.
There is already a lot written about floating point numbers, so I will simply list some facts.
A binary floating point number is represented as: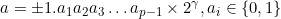 . Operations with an error on floating-point numbers (as opposed to the usual operations on real numbers) are usually designated as:
. Operations with an error on floating-point numbers (as opposed to the usual operations on real numbers) are usually designated as:  . "Machine epsilon" different authors define differently, I will use the following definition:
. "Machine epsilon" different authors define differently, I will use the following definition: 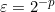 . Note in stl, for example, epsilon is twice as large. Then the error of operations, subject to rounding to the nearest, can be expressed as:
. Note in stl, for example, epsilon is twice as large. Then the error of operations, subject to rounding to the nearest, can be expressed as:
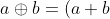(1 + \delta),\ |\delta| \leq \varepsilon)
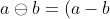(1 + \delta),\ |\delta| \leq \varepsilon)
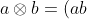(1 + \delta),\ |\delta| \leq \varepsilon)
Calculate the rotation in floating point numbers:
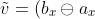 \otimes (c_y \ominus a_y) \ominus (b_y \ominus a_y) \otimes (c_x \ominus a_x)) .
.
Let's move from floating point arithmetic to real arithmetic:
(c_y - a_y)(1 + \delta_1)(1 + \delta_2)(1 + \delta_3) \\ \quad{} & \quad{ } - (b_y - a_y)(c_x - a_x)(1 + \delta_4)(1 + \delta_5)(1 + \delta_6)\bigr](1 + \delta_7).\end{align*})
Now we formulate a sufficient condition for the correctness of the calculation of the sign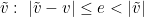 . Imagining a ball centered at
. Imagining a ball centered at 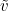 and radius e , we can verify that this condition is correct: the ball will not contain a zero point, therefore, all points of this ball will have one sign, including the point v . It remains to estimate the difference modulus.
and radius e , we can verify that this condition is correct: the ball will not contain a zero point, therefore, all points of this ball will have one sign, including the point v . It remains to estimate the difference modulus. 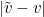 . Open the brackets with deltas and recall that the difference module does not exceed the sum of the modules, and the product module is equal to the product of the modules:
. Open the brackets with deltas and recall that the difference module does not exceed the sum of the modules, and the product module is equal to the product of the modules:
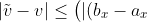(c_y - a_y)| + |(b_y - a_y)(c_x - a_x)|\bigr) \times (4\varepsilon + 6\varepsilon^2 + 4\varepsilon^3 + \varepsilon^4).)
We have obtained the lower bound of the number e in real numbers, but e is a floating point number. notice, that
(c_y - a_y)| + |(b_y - a_y)(c_x - a_x)|\bigr) \times (1 -\varepsilon)^4 \leq\: \qquad{ } \\ \qquad{ } \leq \: |(b_x \ominus a_x)\otimes(c_y \ominus a_y)| \oplus |(b_y \ominus a_y)\otimes(c_x \ominus a_x)|.\end{align*})
From here immediately follows:
\otimes(c_y \ominus a_y)| \oplus |(b_y \ominus a_y)\otimes(c_x \ominus a_x)|\bigr) \times\: \qquad{} \\ \qquad{} \times \: \frac{(4\varepsilon + 6\varepsilon^2 + 4\varepsilon^3 + \varepsilon^4)}{(1 -\varepsilon)^4}.\end{align*})
It’s easy to get a fraction limit from above:
}{(1 -\varepsilon)^4} \leq 8\varepsilon)
This means that the constant e we need can be calculated as follows:
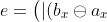\otimes(c_y \ominus a_y)| \oplus |(b_y \ominus a_y)\otimes(c_x \ominus a_x)|\bigr) \times 8\varepsilon.)
Note that the last multiplication, although real, does not derive a number from a set of floating point numbers, since the multiplier is a power of two.
UPD. Thanks Portah and fsgs for the specified typo: the cross function returns not point_2, but double.
UPD2. Mrrl gave an example when it makes sense to rebuild filters to increase performance.
It is possible that many of you have come across the “strange” behavior of implementations of the algorithm of the vychgeoma: crashes and incorrect results. In general, there is nothing surprising in these oddities - these are the costs of transferring continuous geometry to the harsh discrete realities of floating point arithmetic. I would venture to suggest that some of you, by debugging your algorithms, solved similar problems by selecting magical constants. Most likely, if this method and led to the result, it is likely to temporary.
In this article, I will explain how to get rid of the flaws in floating-point calculations with little or no damage to efficiency. Article layout:
- geometric predicate "turn";
- contradictory "naive" implementation of the turn;
- applying interval arithmetic to simplify the predicate calculation;
- long arithmetic and several alternative ways to calculate predicates;
- calculation of the calculation error of rotation in floating point numbers.
So, if you want to know why computational geometry is not a "science of selecting epsilons" and how to correctly and efficiently implement a geometric algorithm, click here.
')
Turn
In general, any algorithm, as a discrete structure, is implemented strictly. Problems arise in conditional blocks where the value of a predicate is checked (for example, if a point lies inside a triangle, if a segment intersects a quadrilateral, etc.).
Consider, for example, a turn, the simplest geometric predicate. This input predicate takes three points on the plane.
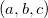 and returns 1 if c lies to the left of the directed segment ab ; -1 if on the right; and 0, if three points lie on one straight line. The predicate is implemented using the vector product:
and returns 1 if c lies to the left of the directed segment ab ; -1 if on the right; and 0, if three points lie on one straight line. The predicate is implemented using the vector product: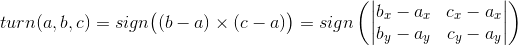
This predicate, despite its simplicity, is very important: it can be used to check, for example, if a pair of segments intersect, if a point lies inside a triangle, etc. Consider its implementation:
enum turn_t {left = 1, right = -1, collinear = 0}; double cross(point_2 const & a, point_2 const & b) { return ax * by - bx * ay; } turn_t turn(point_2 const & a, point_2 const & b, point_2 const & c) { double det = cross(b - a, c - a); if (det > 0) return left; if (det < 0) return right; return collinear; } Consider a call to the turn function with the following input:
point_2 a(3.0, 5.0); point_2 b = -a; point_2 c = a * (1LL << 52); turn_t res = turn(a, b, c); // collinear Despite the fact that all points lie on one straight line, the result, due to the limited accuracy of floating-point arithmetic, is not equal to collinear. Often, as a hot fix, it is believed that the vector product
double det = cross(b - a, c - a); if (det > e) return left; if (det < -e) return right; return collinear; The thought is unsuccessful, since the predicate will be incompatible at four points: for any such constant e, you can choose four points so that the predicate will return contradictory results. For example, consider two parallel, not lying on one straight line segment ab and cd (see figure).

In this figure, the triangles
But note that usually collinear is a rather rare result. If we could produce most of the left and right turns, comparing the vector product with some constant, and counting the rest of the answers in some less effective but accurate way (for example, using long arithmetic), then we could consider our task accomplished, since on average the calculation time of the rotation would increase slightly. The calculation of the constant e, I will give in the appendix below, for those who are not afraid of tedious, but trivial calculations. After the changes, the predicate will look like this:
double l = (bx - ax) * (cy - ay); double r = (cx - ax) * (by - ay); double e = (abs(l) + abs( r)) * std::numeric_limits<double>::epsilon() * 4; double det = l - r; if (det > e) return left; if (det < -e) return right; long_point_2 la(a), lb(b), lc( c); long_t ldet = cross(lb - la, lc - la); if (ldet > 0) return left; if (ldet < 0) return right; return collinear; In general, we have already obtained an absolutely correct and fairly fast predicate. There are two subtleties: firstly, it can be accelerated a little more, and, secondly, the derivation of the formula for the constant e in the general case is quite difficult, despite significant help from symbolic arithmetic (sympy, sage, etc.) .). Now is the time to think about interval arithmetic.
Interval arithmetic
The main idea of interval arithmetic is to fix a real number in a certain segment with floating-point boundaries. Any number that is exactly representable in floating arithmetic will be represented by a degenerate segment - a point.
When two intervals are added, their boundaries are added: the upper boundaries are rounded up (k plus infinity), and the lower ones are rounded down (minus infinity). It is easy to determine the remaining arithmetic operations from the following considerations: the exact value of a real number is unknown, it can be any in the segment. Hence, the resulting segment must contain the results of the arithmetic action on all pairs of numbers from the operand segments.
There are several implementations of interval arithmetic, for example, boost / interval.
Using interval arithmetic, one can much more accurately determine the “confidence interval” of the predicate calculation in floating point arithmetic. Interval arithmetic is, for obvious reasons, two to five times slower than ordinary arithmetic, but about three or four times faster than long arithmetic. So in the implementation of predicates, it makes sense to specify the confidence interval after ordinary floating point arithmetic before calling long arithmetic:
double l = (bx - ax) * (cy - ay); double r = (cx - ax) * (by - ay); double e = (abs(l) + abs( r)) * std::numeric_limits<double>::epsilon() * 4; double det = l - r; if (det > e) return left; if (det < -e) return right; interval_point_2 ia(a), ib(b), ic( c); interval<double> idet = cross(ib - ia, ic - ia); // , , // if (!zero_in(idet)) { if (idet > 0) return left; return right; } long_point_2 la(a), lb(b), lc( c); long_t ldet = cross(lb - la, lc - la); if (ldet > 0) return left; if (ldet < 0) return right; return collinear; Please note that if you remove the usual arithmetic before the interval, the calculation speed will fall two to five times, but not by three or four orders of magnitude, as if we had left only long arithmetic. Sometimes it is much more difficult to estimate the predicate's confidence interval than in this case, and the performance of long arithmetic does not allow it to be used as the main means of calculation. In this case, interval arithmetic will be a reasonable compromise.
About long arithmetic
In general, long arithmetic is not the only way to accurately determine the sign of an arithmetic expression. There are several algorithms that are more efficient than long arithmetic by an order and a half. We are talking about algorithms ESSA and Adaptive Precision Arithmetic. I will not give these algorithms here, since it is easy to find detailed descriptions on the Internet. I will only make a remark that can save some time during debugging: often the coprocessor flags are set in such a way that the calculations are carried out in ten-byte real numbers, which are pushed out to eight or four-byte real numbers when assigned. Due to this, greater accuracy of computations is achieved, but this negatively affects the mentioned ESSA and Adaptive Precision Arithmetic algorithms. As for the rest, these algorithms are quite portable and quite simply realizable.
findings
In this article, I introduced you to the method of filtered predicate calculation. In the first step of the filter (floating point arithmetic), most of the input data is effectively eliminated. In the second step (interval arithmetic), a significant part of the input data that passed the first filter is eliminated. In the third step (long arithmetic, ESSA or Adaptive Precision), the remaining data that has passed through the previous steps is processed. In our tests (a uniform distribution in the square) of their one hundred million input data, approximately two hundred thousand passed on interval arithmetic. Only a few inputs have reached the length of arithmetic, which makes it possible to make an optimistic conclusion about the effectiveness and simplicity of this approach. This approach is generally accepted: it is used, for example, by the library of computational geometry CGAL. In your tasks, you can easily use your own filters, in accordance with the nature of your input data.
Links
- Goldberg. What every computer scientist should know about floating-point arithmetic
- boost / interval library
- Chee K. Yap. Exact geometric computations.
- JR Shewchuk. Adaptive Precision Floating Arrowmetic and Fast Robust Geometric Predicates
Note. Calculating the constant e to rotate
There is already a lot written about floating point numbers, so I will simply list some facts.
A binary floating point number is represented as:
Calculate the rotation in floating point numbers:
Let's move from floating point arithmetic to real arithmetic:
Now we formulate a sufficient condition for the correctness of the calculation of the sign
We have obtained the lower bound of the number e in real numbers, but e is a floating point number. notice, that
From here immediately follows:
It’s easy to get a fraction limit from above:
This means that the constant e we need can be calculated as follows:
Note that the last multiplication, although real, does not derive a number from a set of floating point numbers, since the multiplier is a power of two.
UPD. Thanks Portah and fsgs for the specified typo: the cross function returns not point_2, but double.
UPD2. Mrrl gave an example when it makes sense to rebuild filters to increase performance.
Source: https://habr.com/ru/post/138168/
All Articles