Javascript Prefix Trees

As it was written

One long winter evening, my wife played Bookworm adventures , and periodically kicked me about writing words that were longer than the available letters. A quick search on the Internet for pages that allow to make words from a set of letters gave a bunch of sites that are trying to do it on the server side, and one that does it on a client-side java applet. Those that make up the words of server capacity either have a limit on the size of a set of letters (usually, for some reason at 8), or are deeply thoughtful if they are sent a set of “abcdefghijklmnopqrstuvwxyz”. The Java applet, on the other hand, had a 12-letter limit, worked smartly and almost fit (16 letters are offered in the game for making words).

Next to the java applet, lay a dictionary of 170 thousand English words. Shortly before that, I interviewed and I was assigned a task that was supposed to be solved using prefix trees, then, to my shame, of all the knowledge about prefix trees, only the name remained in my head, and there was no experience with it. Therefore, it was decided to fill this gap.

I make money programming in C ++ , so the original version was written as a console application in C ++ . It worked quickly and correctly, but I didn’t want to scare my wife with a black text box, so it was decided to rewrite it in Javascript. I didn’t want to write the construction of the prefix tree in Javascript, so I added the unloading of the tree in JSON to the existing C ++ program. The output turned out to be a file of 40 megabytes (from the source dictionary of 2 megabytes), maybe at that moment it was worthwhile to score and write the tree construction from the dictionary, but decided to write the search first, since there is a dictionary. Everything worked fine, but loading the page took seconds 5-10 from the hard drive. The construction of the tree was rewritten in Javascript, and the result was somewhat surprising: loading did indeed noticeably faster (this was expected), the surprise was that the browser's memory consumption in this case was three times less. The chromium tab in which the finished prefix tree was loaded ate 150 megabytes of memory, and the one in which the same tree was built from the dictionary only ate 50. As a result, in the final version both boot options are left for comparison. Sources are available on BitBucket .

How it all works

The task is as follows: the user enters a string consisting of letters, it is necessary to find in the dictionary all the words consisting of the letters entered by the user and using each letter no more than once. The user is not forbidden to specify a letter more than once if he wants to find words in which this letter occurs the appropriate number of times.
')
As Wikipedia says ( English is more verbose), a prefix tree is a tree that stores prefixes (that is, the first few letters) of words from the dictionary. The tree structure is such that each subsequent tree level after the root stores the next letter of the prefix relative to the previous level. At the root of the tree is stored an empty prefix that does not contain any letters. If we walk along the path from the root of the tree to any leaf vertex, and write the letters from the visited vertices from left to right, then at the end of the path we will have a word from the dictionary. However, it is worth noting that words do not necessarily end in leaf vertices, for example, a dictionary from the words BAD, CAB, CAD, DAB, AB, AD, BA is represented by the following tree:



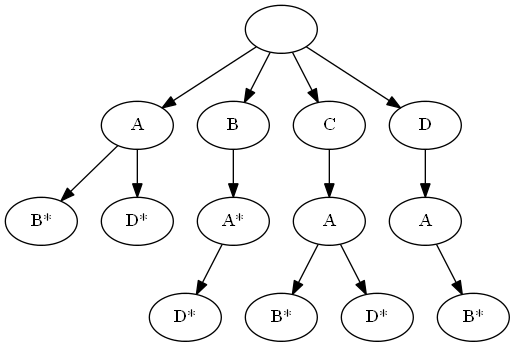
asterisks denote nodes where words end.

So, in the program, the tree is represented by a link to the root node, each node is a Javascript object with data fields, in which the letter corresponding to the node is stored; terminator if this node ends a word; and a number of fields with the name of a single letter with links to the child nodes that store subtrees for the corresponding letter. Those. node A first level of the tree in the picture in the form of JSON looks like this:

 { "data" : "A", "terminator" : false, "B" : { "data" : "B", "terminator" : true }, "D" : { "data" : "D", "terminator" : true } } 

The dictionary is represented as an array of strings. To build a tree, let's start with an empty root node, choose sequentially the words from the dictionary, break into letters and create nodes as necessary:

 var trieRoot; function buildTrie(wordList) { trieRoot = { "data" : "", "terminator" : false }; for ( var i = 0; i < wordList.length; ++i ) { var word = wordList[i]; var letters = word.split(""); var curNode = trieRoot; for ( var j = 0; j < letters.length; ++j ) { if ( curNode[letters[j]] == undefined ) { curNode[letters[j]] = { "data" : letters[j], "terminator" : false }; } curNode = curNode[letters[j]]; } curNode.terminator = true; } } 

To compose words from a set of letters, it is necessary to generate all placements of length from 1 to the number of letters from the list specified by the user. If in the process of constructing the next placement an already constructed prefix is ​​absent in the dictionary, then further construction of the placement can be stopped. The allocations are generated by a simple recursive function, and at the same time the presence of the current prefix is ​​checked in it.

 var letters = []; var used = []; var result = []; var words = {}; function findWords(node, depth) { if ( depth > 0 ) { result[depth - 1] = node.data; if ( node.terminator ) { var word = result.slice(0, depth).join(""); words[word] = 1; } } for ( var i = 0; i < letters.length; ++i ) { var child; if ( !used[i] && (child = node[letters[i]]) != undefined ) { used[i] = true; findWords(child, depth + 1); used[i] = false; } } } 

In the letters array there is a list of letters entered by the user, the used array stores flags for using the appropriate letter of letters from the letters array in the current location. In result the current location is stored, in words - the words found are stored in the object used as an associative array to avoid duplications in the case when the user specifies several repetitions of one letter ("AAABBBCCCDDD").

The rest of the code is dedicated to handling input and output, and has little to do with the relation trees themselves.

Why do you need it

As for me, I can now honestly say that I know what a prefix tree is and faced its practical implementation. In general, practically such a tree can be applied, for example, to store and quickly search for information on the first characters entered (such as search suggestions), the search is very fast, the search time depends only on the prefix length and the size of the alphabet, and if you donate memory, you can get rid of depending on the size of the alphabet.