The use of fuzzy binary relations in solving the problem of appointments (distribution of personnel)
The task of assignments has been known for a long time, the main algorithms for its solution have already been described at Khabarakhabr (see, for example, the Task of assignments ). Nevertheless, the task is still relevant in the distribution of employees according to positions, in the case when there are a lot of employees and positions and criteria, the usual methods will be very laborious.
for the decision maker (DM). Moreover, at the moment, it is possible to use a genetic algorithm and its modification (an interactive genetic algorithm) to solve this problem. That is, there arises a rather complex multi-criteria task of finding the optimal alternative, which can be divided into two tasks. If there is one vacancy, and there are many applicants, then for the decision maker to choose will be effective the use of the method of multi-criteria choice of alternatives using fuzzy inference rules ( Multi-criteria choice of alternatives using fuzzy inference rules. ).
This article attempts to solve the assignment problem in the case of several positions and several vacancies using fuzzy logic methods, namely using fuzzy binary relations. Suggestions / comments / improvements are welcome.
')
So what is a fuzzy relationship?
In the general case, a fuzzy relation or, more precisely, a fuzzy k-ary relation defined on sets (universes) X 1 , X 2 , ..., X k is called some fixed fuzzy subset of the Cartesian product of these universes. In other words, if we denote an arbitrary fuzzy relation by Q, then by definition Q = {<x 1 , x 2 ,. .., x k >, µ Q (<x 1 , x 2 , ..., x k >)}, where µ Q (<x 1 , x 2 , ..., x k >) is the membership function of this fuzzy relation, which is defined as the mapping µ Q : X 1 × X 2 ×… × X k → [0, 1]. Here through <x 1 , x 2 ,. .., x k > is a tuple of k elements, each of which is selected from its own universe: x 1 ϵ X 1 , x 2 ϵ X 2 , ..., x k X k .
Binary fuzzy relation. In the general case, a binary fuzzy relation is defined on the basis sets X1, X2 and is defined as a fuzzy relation Q = {<x i , x j >, μ Q (<x i , x j >)}. Here µ Q (<x i , x j >) is the membership function of the binary fuzzy ratio, which is defined as the map µ Q : X 1 × X 2 → [0, 1], and the <x i , x j > denotes the tuple from two elements, with x 1 ϵ x 1 , x 2 ϵ x 2 .
In addition, to build a solution to the problem, we need the composition of fuzzy binary relations:
The composition of two binary fuzzy relations. Let Q and R be finite or infinite binary fuzzy relations. Moreover, the fuzzy relation Q = {<x i , x j >, μ Q (<x i , x j >)} is given on the Cartesian product of the universums X 1 × X 2 , and the fuzzy relation R = {<x j , x k > , µ R (<x j , x k >)} - on the Cartesian product of the universums X 2 × X 3 . The fuzzy binary relation specified on the Cartesian product X 1 × X 3 and denoted by Q x R is called the composition of binary fuzzy relations Q and R , and its membership function is defined by the following expression:
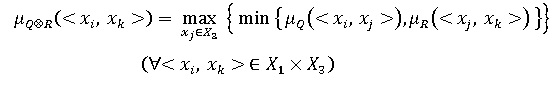
The composition of binary fuzzy relations thus defined is sometimes called the (max-min) -composition or the maximin convolution of fuzzy relations.
Alternative operations of composition of two binary fuzzy relations. The fuzzy binary relation specified on the Cartesian product X 1 × X 3 and denoted by Q * R is called (max - *) - the composition of binary fuzzy relations Q and R , if its membership function is defined by the following expression:

In particular, if in this expression instead of the operation “*” we use the operation of algebraic multiplication, then we get the definition of (max-prod) -composition.
(min-max) -composition. The fuzzy binary relation specified on the Cartesian product X 1 × X 3 and denoted by Q + R is called the (min-max) composition of the binary fuzzy relations Q and R if its membership function is defined by the following expression:

We now turn directly to the problem. This method was developed to solve a specific task in the field of personnel management, therefore I will describe its work immediately using the example of this task.
So, there are two sets: a set of positions and their profiles and a set of employees, which should be distributed as effectively as possible. Thus, the input data are the data sets, and output - the degree of compliance of candidates with positions.
In connection with the foregoing, consider a fuzzy model based on two binary fuzzy relations Ϯ and Ψ . The first of these fuzzy relations is based on two basic sets X = {x 1 , ..., x n } and Y = {y 1 , ..., y m }, and the second - on two basic sets Y = {y 1 , ..., y m } and Z = {z 1 , ..., z l }. Here X describes the set of specialties for which recruitment is carried out, Y - the set of characteristics (properties) of positions and Z - the set of candidates for positions. In the context of interest to us, a fuzzy attitude Ϯ meaningfully describes the profiles of specialties, and Ψ - profiles of candidates for positions. To determine the suitability of candidates for positions, we use the compositions of the original fuzzy relations. So, (max-min) - and (max-prod) -compositions (see clause 2.2) provide information on the degree of compliance of the candidate with the vacancy and the possibility of his appointment, and (min-max) -composition probably allows you to identify an employee who does not fit for this job.
Thus, three models are applied:
A small program was written to count these compositions, but I will not describe it here, since it is very simple (working with matrices) and the post is already very long. We turn immediately to the experiments with the program.
Consider a fuzzy model based on two binary fuzzy relations Ϯ and Ψ . The first of these fuzzy relations is based on two basic sets X and Y, and the second on two basic sets Y and Z. Here X describes the many specialties for which recruitment is carried out, Y - the set of psycho-physiological characteristics and Z - the set of candidates for posts. In the context of interest to us, fuzzy attitude Ϯ meaningfully describes the psycho-physiological profiling of specialties, and Ψ - the psycho-physiological profiling of candidates for posts. For concreteness, let X = {manager, programmer, driver, secretary-assistant, translator}; Y = {speed and flexibility of thinking, ability to make decisions quickly, stability and concentration of attention, visual memory, responsiveness, motor memory, physical endurance, coordination of movements, emotional-volitional stability, responsibility}; Z = {Petrov, Ivanov, Sidorov, Vasilyeva, Grigorieva}. The specific values of the membership functions μ Ϯ (<x i , y j >) and μ (<y j , z k >) of the fuzzy relations under consideration are presented in the following tables (Table 3.1 and 3.2).

Since the relations in question satisfy the formal requirements necessary to fulfill their fuzzy composition, the result of the operation of a fuzzy composition can be represented as

Analysis table. 3.3 shows that the HR manager can be recommended to recommend people to be appointed to the following positions (based on the maximum values of the membership function of the composition of the fuzzy relationships in question): Petrov is a manager, driver; Ivanov - manager, secretary; Sidorov - the driver; Vasilyeva - manager, Grigorieva - manager. From the point of view of assigning the employees to the manager’s place, the most suitable candidates are: Petrov, Ivanov, Vasilyeva and Grigorieva; in the specialty programmer - the same candidates; for the position of driver - Sidorov; for the post of secretary Ivanov; to work as a translator - Sidorov and Vasiliev.
Now consider the fuzzy composition of the original fuzzy relations.

Analysis table. 3.4 shows, the HR-manager can be recommended to recommend people to be appointed to the following positions (based on the maximum values of the membership function of the composition of the fuzzy relationships in question): Petrov is the driver; Ivanov - manager, secretary; Sidorov - the driver; Vasilyeva - manager, Grigorieva - manager. From the point of view of assigning the employees to the manager’s place, the most suitable candidates are: Ivanov and Grigorieva; in programmer specialty Grigorieva; in the specialty driver - Petrov; Specialty Secretary - Ivanov; specialty translator - Sidorov and Vasilyeva.
Following the general recommendations of applied systems analysis regarding the principle of multi-model, we can draw the following conclusion. If using different models obtained the same results. This fact may indicate the presence of a stable connection or pattern between the individual elements of the models. As applied to the considered fuzzy models, the coincidence of results. obtained on the basis of operations (max-min) -composition and (max-pd) -composition, gives the basis for more confident conclusions regarding the choice of certain specialties for training candidates.
At the end of this test we will analyze the results obtained as a result of the (min-max) composition of the original fuzzy relations.

Analyze the data. Since for fuzzy sets, in fact, the main values of the membership function are 0 and 1, and the worst option in terms of conclusions is 0.5, which cannot provide an informative answer to the question about the candidate’s inconsistency with the position.
Thus, based on the analysis of the three compositions, we can conclude that the data obtained using (max-min) - and (max-prod) -compositions were supplemented and refined, and the (min-max) -composition of two fuzzy mappings was somewhat divergent with them. So for example, according to the results of the first two compositions, Sidorov is suitable for the position of a driver, but according to (min-max) -compositions, it is not very suitable.
For today, I think everything. However, I conducted tests with other data and obtained results that are quite difficult to analyze, that is, such an approach to solving a problem does not always give an unambiguous result and needs to be improved.
for the decision maker (DM). Moreover, at the moment, it is possible to use a genetic algorithm and its modification (an interactive genetic algorithm) to solve this problem. That is, there arises a rather complex multi-criteria task of finding the optimal alternative, which can be divided into two tasks. If there is one vacancy, and there are many applicants, then for the decision maker to choose will be effective the use of the method of multi-criteria choice of alternatives using fuzzy inference rules ( Multi-criteria choice of alternatives using fuzzy inference rules. ).
This article attempts to solve the assignment problem in the case of several positions and several vacancies using fuzzy logic methods, namely using fuzzy binary relations. Suggestions / comments / improvements are welcome.
')
So what is a fuzzy relationship?
In the general case, a fuzzy relation or, more precisely, a fuzzy k-ary relation defined on sets (universes) X 1 , X 2 , ..., X k is called some fixed fuzzy subset of the Cartesian product of these universes. In other words, if we denote an arbitrary fuzzy relation by Q, then by definition Q = {<x 1 , x 2 ,. .., x k >, µ Q (<x 1 , x 2 , ..., x k >)}, where µ Q (<x 1 , x 2 , ..., x k >) is the membership function of this fuzzy relation, which is defined as the mapping µ Q : X 1 × X 2 ×… × X k → [0, 1]. Here through <x 1 , x 2 ,. .., x k > is a tuple of k elements, each of which is selected from its own universe: x 1 ϵ X 1 , x 2 ϵ X 2 , ..., x k X k .
Binary fuzzy relation. In the general case, a binary fuzzy relation is defined on the basis sets X1, X2 and is defined as a fuzzy relation Q = {<x i , x j >, μ Q (<x i , x j >)}. Here µ Q (<x i , x j >) is the membership function of the binary fuzzy ratio, which is defined as the map µ Q : X 1 × X 2 → [0, 1], and the <x i , x j > denotes the tuple from two elements, with x 1 ϵ x 1 , x 2 ϵ x 2 .
In addition, to build a solution to the problem, we need the composition of fuzzy binary relations:
The composition of two binary fuzzy relations. Let Q and R be finite or infinite binary fuzzy relations. Moreover, the fuzzy relation Q = {<x i , x j >, μ Q (<x i , x j >)} is given on the Cartesian product of the universums X 1 × X 2 , and the fuzzy relation R = {<x j , x k > , µ R (<x j , x k >)} - on the Cartesian product of the universums X 2 × X 3 . The fuzzy binary relation specified on the Cartesian product X 1 × X 3 and denoted by Q x R is called the composition of binary fuzzy relations Q and R , and its membership function is defined by the following expression:
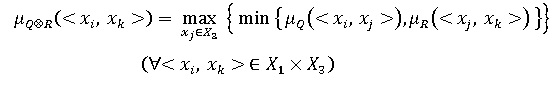
The composition of binary fuzzy relations thus defined is sometimes called the (max-min) -composition or the maximin convolution of fuzzy relations.
Alternative operations of composition of two binary fuzzy relations. The fuzzy binary relation specified on the Cartesian product X 1 × X 3 and denoted by Q * R is called (max - *) - the composition of binary fuzzy relations Q and R , if its membership function is defined by the following expression:

In particular, if in this expression instead of the operation “*” we use the operation of algebraic multiplication, then we get the definition of (max-prod) -composition.
(min-max) -composition. The fuzzy binary relation specified on the Cartesian product X 1 × X 3 and denoted by Q + R is called the (min-max) composition of the binary fuzzy relations Q and R if its membership function is defined by the following expression:

We now turn directly to the problem. This method was developed to solve a specific task in the field of personnel management, therefore I will describe its work immediately using the example of this task.
So, there are two sets: a set of positions and their profiles and a set of employees, which should be distributed as effectively as possible. Thus, the input data are the data sets, and output - the degree of compliance of candidates with positions.
In connection with the foregoing, consider a fuzzy model based on two binary fuzzy relations Ϯ and Ψ . The first of these fuzzy relations is based on two basic sets X = {x 1 , ..., x n } and Y = {y 1 , ..., y m }, and the second - on two basic sets Y = {y 1 , ..., y m } and Z = {z 1 , ..., z l }. Here X describes the set of specialties for which recruitment is carried out, Y - the set of characteristics (properties) of positions and Z - the set of candidates for positions. In the context of interest to us, a fuzzy attitude Ϯ meaningfully describes the profiles of specialties, and Ψ - profiles of candidates for positions. To determine the suitability of candidates for positions, we use the compositions of the original fuzzy relations. So, (max-min) - and (max-prod) -compositions (see clause 2.2) provide information on the degree of compliance of the candidate with the vacancy and the possibility of his appointment, and (min-max) -composition probably allows you to identify an employee who does not fit for this job.
Thus, three models are applied:
- max-min - model
- max-prod - model
- min-max - model
A small program was written to count these compositions, but I will not describe it here, since it is very simple (working with matrices) and the post is already very long. We turn immediately to the experiments with the program.
Consider a fuzzy model based on two binary fuzzy relations Ϯ and Ψ . The first of these fuzzy relations is based on two basic sets X and Y, and the second on two basic sets Y and Z. Here X describes the many specialties for which recruitment is carried out, Y - the set of psycho-physiological characteristics and Z - the set of candidates for posts. In the context of interest to us, fuzzy attitude Ϯ meaningfully describes the psycho-physiological profiling of specialties, and Ψ - the psycho-physiological profiling of candidates for posts. For concreteness, let X = {manager, programmer, driver, secretary-assistant, translator}; Y = {speed and flexibility of thinking, ability to make decisions quickly, stability and concentration of attention, visual memory, responsiveness, motor memory, physical endurance, coordination of movements, emotional-volitional stability, responsibility}; Z = {Petrov, Ivanov, Sidorov, Vasilyeva, Grigorieva}. The specific values of the membership functions μ Ϯ (<x i , y j >) and μ (<y j , z k >) of the fuzzy relations under consideration are presented in the following tables (Table 3.1 and 3.2).

Since the relations in question satisfy the formal requirements necessary to fulfill their fuzzy composition, the result of the operation of a fuzzy composition can be represented as

Analysis table. 3.3 shows that the HR manager can be recommended to recommend people to be appointed to the following positions (based on the maximum values of the membership function of the composition of the fuzzy relationships in question): Petrov is a manager, driver; Ivanov - manager, secretary; Sidorov - the driver; Vasilyeva - manager, Grigorieva - manager. From the point of view of assigning the employees to the manager’s place, the most suitable candidates are: Petrov, Ivanov, Vasilyeva and Grigorieva; in the specialty programmer - the same candidates; for the position of driver - Sidorov; for the post of secretary Ivanov; to work as a translator - Sidorov and Vasiliev.
Now consider the fuzzy composition of the original fuzzy relations.

Analysis table. 3.4 shows, the HR-manager can be recommended to recommend people to be appointed to the following positions (based on the maximum values of the membership function of the composition of the fuzzy relationships in question): Petrov is the driver; Ivanov - manager, secretary; Sidorov - the driver; Vasilyeva - manager, Grigorieva - manager. From the point of view of assigning the employees to the manager’s place, the most suitable candidates are: Ivanov and Grigorieva; in programmer specialty Grigorieva; in the specialty driver - Petrov; Specialty Secretary - Ivanov; specialty translator - Sidorov and Vasilyeva.
Following the general recommendations of applied systems analysis regarding the principle of multi-model, we can draw the following conclusion. If using different models obtained the same results. This fact may indicate the presence of a stable connection or pattern between the individual elements of the models. As applied to the considered fuzzy models, the coincidence of results. obtained on the basis of operations (max-min) -composition and (max-pd) -composition, gives the basis for more confident conclusions regarding the choice of certain specialties for training candidates.
At the end of this test we will analyze the results obtained as a result of the (min-max) composition of the original fuzzy relations.

Analyze the data. Since for fuzzy sets, in fact, the main values of the membership function are 0 and 1, and the worst option in terms of conclusions is 0.5, which cannot provide an informative answer to the question about the candidate’s inconsistency with the position.
Thus, based on the analysis of the three compositions, we can conclude that the data obtained using (max-min) - and (max-prod) -compositions were supplemented and refined, and the (min-max) -composition of two fuzzy mappings was somewhat divergent with them. So for example, according to the results of the first two compositions, Sidorov is suitable for the position of a driver, but according to (min-max) -compositions, it is not very suitable.
For today, I think everything. However, I conducted tests with other data and obtained results that are quite difficult to analyze, that is, such an approach to solving a problem does not always give an unambiguous result and needs to be improved.
Source: https://habr.com/ru/post/137461/
All Articles