Calculation errors in the vicinity of machine zero
Periodically on Habré there are great articles about the intricacies of floating point arithmetic. Actually, the mentioned publication was one of the first sources read in attempts to deal with the problem. This did not immediately become clearer, but nevertheless, the organization of neural connections somehow got streamlined. Get to the point.
The problem was formed when performing calculations in the framework of a single project and a future master's thesis on the hydrodynamics of a porous medium. I don’t hide the fact that the roots are hidden partly in the author’s personal curvature and neglecting commonplace known tips regarding the processing of small numbers, but nevertheless, this led to quite interesting observations and reflections.
If we discard the physical essence, the task is to solve the system of seven partial differential equations. Said and done, there is no difficulty in this particular - we write an explicit finite-difference scheme, parallelize on OpenMP and after final syntax debugging and speed optimization “the machine starts to rustle” .
')
Computational configuration: an HP 550 with a Core 2 Duo 1.8 GHz onboard, running Ubuntu 11.04.
Compilers: gfortran 4.5.2 and Intel Fortran Compiler 12.1.0.
In the initial conditions, it is assumed that there is no water in the liquid state inside the calculated area — it appears during phase transformations. And it is precisely this absence that played the main role in our performance.
So, there is no water in the area. What do you want to write in the initial condition? Naturally, 0.0D + 00 was immediately written (the program was written with double precision of real numbers). The account at the initial stages goes in the immediate vicinity of the machine zero. What are the results? Let's look at the chart:
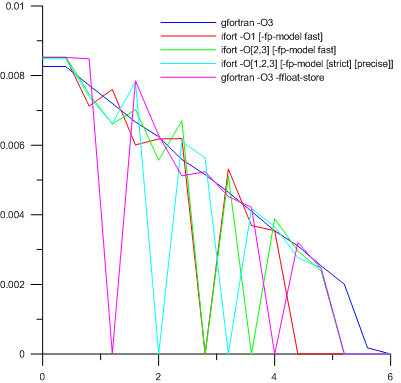
Here is the pore saturation distribution with water along the coordinate in the most interesting part of the computational domain after a little more than a day of the physical time of the model.
The necessary digression about the signatures in the legend of the schedule: a total of 18 different key combinations were tested (6 for gfortran and 12 for ifort), but many of them gave exactly the same results, and therefore were combined. The square brackets in the legend mean that any of the options contained in them could have been written. For example, “encryption” -O [1,2,3] [-fp-model [strict] [precise]] says that the compiler was used with the optimization of all possible levels, and in addition one floating-point model could be included (and could not be included). Three options (two from -fp-model and one without it) multiplied by three levels of optimization - a total of nine combinations. All of them were equivalent.
And now the result. Something realistic and physically possible was obtained only on gfortran without the inclusion of compliance with the IEEE 754 standard (key -ffloat-store). The rest of the chaos of lines does not contain a single drop of physical meaning, because even mathematically, equations do not allow this. The initially suspected instability of the difference scheme was justified, since no methods of dealing with it were successful.
It was noted that when water is available at the initial moment, the score remains stable and the differences between options and compilers are hidden in the vicinity of the sixth significant digit. And since According to the graphs obtained, the characteristic orders of magnitude should be around 1.0e-2, then a non-zero value was entered into the initial condition, but very small. The selection was able to establish that for 8-byte real it should be at least 1.0e-21. And then:
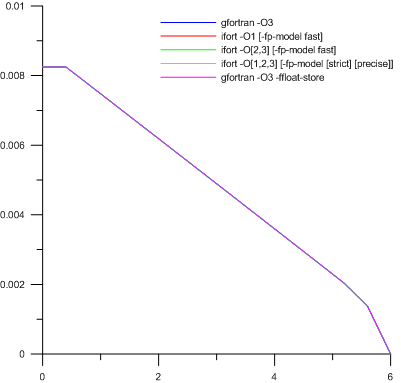
Yes, here, as written in the legend, in fact, five graphs. Simply, we get the very difference within the sixth significant figure.
The reasons? Quite obvious. They lie in the intricacies of the simultaneous processing of large and small numbers. And the fact that the phenomenon is so significant in scale was, in general, expected. But, above all, the interest is caused by the instability of the work of a truly excellent tool from Intel against the background of the relative success of gfortran 4.5.2. It should be noted that similar problems were also found when calculating the old version of gfortran 4.1.2 with optimization turned on and without other options installed on the available cluster (running Slamd64), but they were not given due attention at that time.
Compliance with IEEE 754, oddly enough, played a critical role for gfortran. Without it, the bill is fairly stable and accurate. For the brainchild of Intel, this turned out to be not so significant, because it did not work correctly anyway.
So, the conclusions and thoughts about the causes of what he saw.
Compiler testing for IEEE 754 compliance was performed using FORTRAN-version of William Kahan's “Floating point paranoia”.
The problem was formed when performing calculations in the framework of a single project and a future master's thesis on the hydrodynamics of a porous medium. I don’t hide the fact that the roots are hidden partly in the author’s personal curvature and neglecting commonplace known tips regarding the processing of small numbers, but nevertheless, this led to quite interesting observations and reflections.
If we discard the physical essence, the task is to solve the system of seven partial differential equations. Said and done, there is no difficulty in this particular - we write an explicit finite-difference scheme, parallelize on OpenMP and after final syntax debugging and speed optimization “the machine starts to rustle” .
')
Computational configuration: an HP 550 with a Core 2 Duo 1.8 GHz onboard, running Ubuntu 11.04.
Compilers: gfortran 4.5.2 and Intel Fortran Compiler 12.1.0.
In the initial conditions, it is assumed that there is no water in the liquid state inside the calculated area — it appears during phase transformations. And it is precisely this absence that played the main role in our performance.
So, there is no water in the area. What do you want to write in the initial condition? Naturally, 0.0D + 00 was immediately written (the program was written with double precision of real numbers). The account at the initial stages goes in the immediate vicinity of the machine zero. What are the results? Let's look at the chart:

Here is the pore saturation distribution with water along the coordinate in the most interesting part of the computational domain after a little more than a day of the physical time of the model.
The necessary digression about the signatures in the legend of the schedule: a total of 18 different key combinations were tested (6 for gfortran and 12 for ifort), but many of them gave exactly the same results, and therefore were combined. The square brackets in the legend mean that any of the options contained in them could have been written. For example, “encryption” -O [1,2,3] [-fp-model [strict] [precise]] says that the compiler was used with the optimization of all possible levels, and in addition one floating-point model could be included (and could not be included). Three options (two from -fp-model and one without it) multiplied by three levels of optimization - a total of nine combinations. All of them were equivalent.
And now the result. Something realistic and physically possible was obtained only on gfortran without the inclusion of compliance with the IEEE 754 standard (key -ffloat-store). The rest of the chaos of lines does not contain a single drop of physical meaning, because even mathematically, equations do not allow this. The initially suspected instability of the difference scheme was justified, since no methods of dealing with it were successful.
It was noted that when water is available at the initial moment, the score remains stable and the differences between options and compilers are hidden in the vicinity of the sixth significant digit. And since According to the graphs obtained, the characteristic orders of magnitude should be around 1.0e-2, then a non-zero value was entered into the initial condition, but very small. The selection was able to establish that for 8-byte real it should be at least 1.0e-21. And then:

Yes, here, as written in the legend, in fact, five graphs. Simply, we get the very difference within the sixth significant figure.
The reasons? Quite obvious. They lie in the intricacies of the simultaneous processing of large and small numbers. And the fact that the phenomenon is so significant in scale was, in general, expected. But, above all, the interest is caused by the instability of the work of a truly excellent tool from Intel against the background of the relative success of gfortran 4.5.2. It should be noted that similar problems were also found when calculating the old version of gfortran 4.1.2 with optimization turned on and without other options installed on the available cluster (running Slamd64), but they were not given due attention at that time.
Compliance with IEEE 754, oddly enough, played a critical role for gfortran. Without it, the bill is fairly stable and accurate. For the brainchild of Intel, this turned out to be not so significant, because it did not work correctly anyway.
So, the conclusions and thoughts about the causes of what he saw.
- The most likely candidate for the role of the cause of the observed behavior of calculations seems to be the subtleties of rounding numbers. Because in the initial distribution of the value, a zero value is specified, then in the first steps the count is made almost at the boundary of machine accuracy. Accordingly, this leads to the accumulation of noticeable errors, which manifest themselves in the final result.
- The loss of accuracy in the algorithm is obviously caused by the fact that the dimensional system of seven differential equations in partial derivatives is solved, the variables in each of which have their own characteristic values that are significantly different from the others. With the right choice of scale factors, in a dimensionless system of equations to get close at least in order of magnitude values of all variables, although during initial attempts to make the dimensionless, there were small coefficients in front of the derivatives, which was the reason for the rejection of this procedure.
- The question of why gfortran, which does not meet the standard for floating-point calculations, is capable of producing an acceptable result, remains open. It is reasonable to assume that there are some own, different from the standard, rounding rules that ensure the preservation of a stable account, as well as their adjustment and refinement in the compiler development process. “Fragile balance of mistakes” or a well-considered correction of the approach? Alas, at my level of knowledge about the toolkit, aimed primarily at the use of compilers, rather than testing them and studying properties, this is unknown. But it makes one think and remember the warnings about possible loss of accuracy in various places of the programs, given at the first stages of teaching numerical methods at the university.
Compiler testing for IEEE 754 compliance was performed using FORTRAN-version of William Kahan's “Floating point paranoia”.
Source: https://habr.com/ru/post/137000/
All Articles