Simplex Sierpinski

This article is intended to familiarize you with the basic mathematical component of computer multidimensional graphics. Using the example of the Sierpinski simplex , the article discusses the issues of constructing, moving, projecting and displaying complex multidimensional geometric figures.
There are also pictures, videos, sources, and I assure you that everything is very simple, read, understand.

What is the Sierpinski triangle , and what the Sierpinski pyramid is quite understandable. But what is the Sierpinski simplex? To begin with, for those who have not read on the wiki what simplex is, I’ll just say that simplex is an n-dimensional tetrahedron (see video ). Well, the Sierpinski simlex is a kind of fractal, built by analogy with the Sierpinski triangle and tetrahedron.

Construction of an equilateral simplex

Do not believe it, but this is the most difficult among all that is in this article (according to my estimates). But all we need is n points in n-1 dimensional space, equidistant from each other and from the center. Before reading further, I strongly recommend to think, how would you build such points?
')
Of course, we are interested in cases where n> = 3, otherwise it’s just not interesting. Each n-th point will be built on the basis of all previous ones. To begin with, we need to build a normal equilateral triangle:


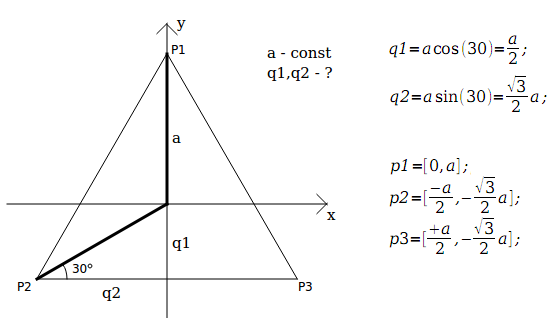
In order to add a new point - you need a new dimension (denoted by W). Entering this measurement, so that the point is equidistant from all other points, set the value of the point P1 for this point P1 along the W axis, and the rest of the points along the W axis as -q2. The remaining coordinates of the axes for the point Pn are left zero. What is the result? With all the points that were - remain at equal distance from each other and from the center, and the new point is equidistant from all the others. It remains only to choose such q1, q2, so that all points are equidistant from each other, and from the center.


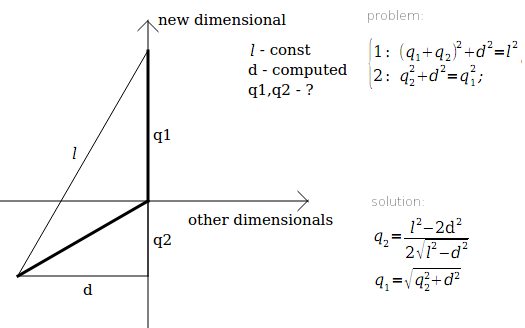
l - the distance between points is constant, and is calculated after constructing a triangle.
d - distance from points to the center - changes, and is calculated before adding a new point.
The first equation indicates that the distances from the received points to the new ones should be the same.
The second is that the distances to the center should be the same.
Actually, this is how we get an equilateral simplex.

Sources:

double c = r * sqrt(3) / 2; double l = c * 2; //distance between points points[0][0] = + 0; points[0][1] = + r; //first point points[1][0] = + c; points[1][1] = - r / 2; //second point points[2][0] = - c; points[2][1] = - r / 2; //3th point for (int i = 3; i <= dimensionalCount; i++) { double d = points[0].distanceToCenter(); double q2 = (l * l - 2 * d * d) / (2 * sqrt(l * l - d * d)); double q1 = sqrt(d * d + q2 * q2); for (int k = 0; k < i; k++) { points[k][i-1] = -q2; //set i-th dimension for all created points points[i][k] = 0; //set all calculated dimension for new point } points[i][i-1] = q1; } 

Fractal

It is very easy to see that both the triangle (n = 2) and the tetrahedron (n = 3) of Sierpinski are created from the base figure by replacing the base figure with n + 1 of the same, but smaller. In each of the new figures, one point of the base figure is taken as a basis, the remaining points are the centers of mass of the segments, which include this point. In principle, everything is very simple and clear.

So we write:

 void rec(QVector<Simplex>& storage, const Simplex& current, int recursionDepth) { if (recursionDepth == maxRecursionDepth) storage.append(current); else { for (int i = 0; i <= n; i++) { Simplex newTriangle(current.dimensionsCount()); for (int k = 0; k <= n; k++) { if (i == k) newTriangle[k] = current[i]; else newTriangle[k] = (current[i] + current[k]) / 2.0; } rec(storage, newTriangle, recursionDepth + 1); } } } 

As you can see, nowhere is there a reliance on the dimension of space, and it works correctly for both 2D and 3D:

Rotate & Projection

It can be difficult to rotate (quaternions, matrix transformations), but you can simply ... We will do everything simply, sequentially rotate in each two coordinates. For 2D, this can be perceived as a turn around a point, for 3D - around a straight line, for ND - around (N-2) -dimensional space. Actually, the rotation formula is calculated very simply:


Well, it is programmed even easier:

  for (int i = 0; i < coordinates.count(); i++) for (int k = i + 1; k < coordinates.count(); k++) { ratio = sqrt(2 + i * coordinates.count() + k); p1 = temp[i] * cos(angle * ratio) - temp[k] * sin(angle * ratio); p2 = temp[k] * cos(angle * ratio) + temp[i] * sin(angle * ratio); temp[i] = p1; temp[k] = p2; } 

Where ratio is the ratio in order for the rotation in different directions to be at different speeds, preferably without looping. temp [i] is the i-th coordinate of the current point.

Projection is the most difficult moment of working with multidimensional spaces. There are many reasons:
1. No one used to understand multidimensional geometric objects.
2. Optics of physics is silent about this (as far as I know).
3. A bunch of different methods and all overload the picture, and it is unclear what is correct.

We take the simplest method - a perspective projection. We will project the n-dimensional point on the (n-1) space ... Thus, each time lowering the N - we get to the point that the point is already two-dimensional or three-dimensional and can already be displayed.

Using the example of 2D to 1D, we will try to calculate the perspective projection formula.


It can be seen that with the help of 2 coordinates and a certain focus constant one coordinate can be made. And the formula is very simple, like the code:

  for (int i = coordinates.count() - 1; i > 3; i--) for (int k = 0; k < i; k++) temp[k] *= focus / (focus + temp[i]); 

How is all this correct? Not at all correctly, never, not a drop! But judging by what is in the internet, something very similar is used by other programmers. For example, a tesseract obtained by this projection method:

Rendering

QPainter is the easiest way, which is to use standard development environment tools to draw everything with normal lines, without lighting, filling triangles, and so on. In my sources, it is enabled by default, and will work wherever there is Qt (Windows, Linux, Mac OS ...).

Actually, this is how the rendering code looks like:

  QPoint center(this->width() / 2, this->height() / 2); foreach(const Simplex& simplex, simplexes) for (int i = 0; i < simplex.dimensionsCount() + 1; i++) for (int k = i+1; k < simplex.dimensionsCount() + 1; k++) p.drawLine(simplex[i].to2D(focus, angle) + center, simplex[k].to2D(focus, angle) + center); 

As you can see, there is nothing simpler ... But we need to be beautiful, right?

OpenGL , DirectX is a progressive method that allows rendering everything in real time beautifully. But there is a misfortune: without transparency, nothing will be beautiful, and the transparency of these two monsters suggests that you need to render from the far (z -> max) to the close (z -> min). For this, each frame, the triangles need to be sorted, and in my example they are about 6000. Well, it does not matter, the trouble is that in general it is impossible to determine which triangle is closer and which is farther. Moreover, when we speak of projection from multidimensional space, we say that the triangles intersect. As a result, they need to cut and sort each iteration, which is already very difficult ...
I did not implement this method.

Ray tracing is what the doctor prescribed. This technology will allow you to get the picture of the highest quality and has a drawback only in speed. But, in fact, we don’t need real time.

For tracing, I used POV-Ray , which was ideally suited for this task only because it can run from the command line, without any GUI there.
To use this miracle, I wrote a certain template, which the program fills with the necessary points, and the output is a ready-for-trace .pov file. The pattern on a set of points builds triangles and frames, and is very simple in its structure:

 #declare ppp = array[<<!!--count of points--!!>>] { <<!!--Main Array of points--!!>> }; #declare i = 0; #while(i < <<!!--count of points--!!>>) #if (vlength(ppp[i] - ppp[i+1])!=0) cylinder{ppp[i], ppp[i+1], 0.2 texture {pigment{color Gray}} } #end #if (vlength(ppp[i] - ppp[i+2])!=0) cylinder{ppp[i], ppp[i+2], 0.2 texture {pigment{color Gray}} } #end #if (vlength(ppp[i+1] - ppp[i+2])!=0) cylinder{ppp[i+1], ppp[i+2], 0.2 texture {pigment{color Gray}} } #end polygon {4 ppp[i], ppp[i+1], ppp[i+2] ,ppp[i] texture { Surface_Texture }} #declare i=i+3; #end 

Actually, based on this template, 1000 pictures were made with different turns, of which this video was later made:


Sources

The article is dedicated to the girls heavy metal band Fight with Fate.