HashLife on the knee
After messing around with the three-dimensional game “Life”, I remembered that for the regular, Konevsky version of this game, there is an algorithm called “Hashlife” . It is described in several phrases on Wikipedia, and the picture with a comment there (“configuration after 6 octillion generations”) was enough for me to keep away from this idea: how many resources does this algorithm need? Is it worth it to take at all?
The general idea of the algorithm is as follows.
Suppose that we have a square of a field of size N * N (N> = 4 - the power of two). Then we can uniquely determine the state of its central region of size (N / 2) * (N / 2) in terms of T = N / 4 steps. If we remember the state of the original square and the result of its evolution in the dictionary, then we will be able next time, having met such a square, to immediately determine what will become of it.
')
Suppose that for squares N * N, we can count the evolution by N / 4 steps. Suppose we have a square 2N * 2N. To calculate its development on N / 2 steps, you can do the following.
We divide the square into 16 squares with side N / 2. Let's make one of them 9 squares with side N, for each of them we will find the result of evolution by N / 4 steps. It turns out 9 squares with side N / 2. In turn, we will make 4 squares with a side N of them, and for each of them we will find the result of an evolution by N / 4 steps. The resulting 4 squares with a side of N / 2 will be combined into a square with a side of N - it will be the answer.
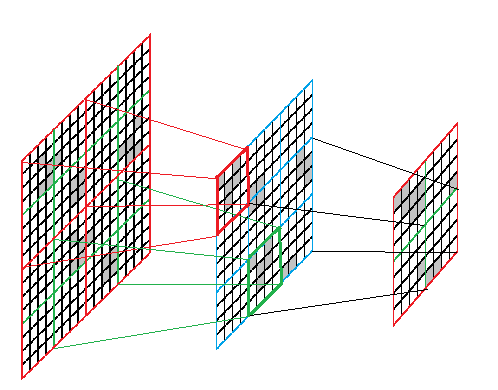
To implement the algorithm, we need to be able to do the following:
If you look for the result of evolution at the time of building the square, then it is enough to have a structure with 5 fields:
Then the algorithm of combining four squares into one can be written as:
Actually, everything. Little things left:
Stop recursion. To do this, all 4 * 4 squares are entered into the dictionary and the results of their evolution are 1 step (in fact, only in this place the program requires knowledge of the rules of the game). For 2 * 2 squares, the evolution by half a step is not calculated, they are marked in some special way.
Double the number of evolutionary steps. In terms of the algorithm, this is the same as double the size of the square containing the original field. If we want to leave the square in the center, adding zeros to it, you can do this:
Here Zero is a special square, all parts and the result of which is equal to itself.
And you can simply alternate the actions x = Unite (x, Zero, Zero, Zero) and x = Unite (Zero, Zero, Zero, x). The original square will be somewhere in the center.
Implement a dictionary. Here I did not find a beautiful solution: I need to search for an object by key, which is 80% of this object (and not only the remaining 20%, but also the object itself must be searched for). Fumbling with different types of collections, I waved my hand and entered Fortran: I described five integer arrays (LT, RT, LB, RB, Res) and said that the square is determined by an integer – index in these arrays. Indices from 0 to 15 are reserved for squares 2 * 2. The sixth array, twice as long, is used for hashing.
You also need to set the field and read the result - but this is a matter of technology. Although reading must be careful: if you run Expand more than 63 times, the length of the side of the field will no longer fit into 64 bits.
I tried the algorithm on such constructions:
"Garbage bin".

It moves at c / 2 speed, reserves a lot of garbage behind it and releases a pair of gliders every 240 steps. A trillion generations (more precisely, 2 ^ 40) were calculated in 0.73 seconds. Approximately 120000 squares fell into the dictionary (1500 for each doubling of time), the number of living cells per field was 600 billion.
A fragment of the resulting field looks like this:
(2001x2001, 82 KB)
"The battle of glider guns"
Two glider guns are located at a distance of 800 cells from each other, the flows released by them collide:
(T = 2048, 804x504, 11 KB)
Shortly after the collision, gliders fly out of a heap of debris, which first destroy one gun:
(T = 4096, 1098x1024, 30 Kb)
And then the second (after which the development quickly ends):
(T = 8192, 3146x3252, 190 Kb)
The counting time is 0.84 seconds, the number of elements in the dictionary is about 270,000.
"Random Filling"
Field 1024 * 1024 is randomly filled with cells with a density of 1/3. For the algorithm, this is the most difficult case: the configuration stabilizes slowly, and the squares do not begin to repeat immediately.
Here is an example of the development of one of the configurations:
(T = 0, 1024x1024, 300 Kb)
(T = 1024, 1724x1509, 147 Kb)
(T = 2048, 2492x2021, 177 Kb)
(T = 4096, 4028x3045, 300 Kb)
(T = 8192, 7100x5093, 711 Kb)
The counting time is 14 seconds, the number of elements in the dictionary is about 15 million, about 35,000 points remained on the field.
What is unusual about this algorithm? I would note the following:
The general idea of the algorithm is as follows.
Suppose that we have a square of a field of size N * N (N> = 4 - the power of two). Then we can uniquely determine the state of its central region of size (N / 2) * (N / 2) in terms of T = N / 4 steps. If we remember the state of the original square and the result of its evolution in the dictionary, then we will be able next time, having met such a square, to immediately determine what will become of it.
')
Suppose that for squares N * N, we can count the evolution by N / 4 steps. Suppose we have a square 2N * 2N. To calculate its development on N / 2 steps, you can do the following.
We divide the square into 16 squares with side N / 2. Let's make one of them 9 squares with side N, for each of them we will find the result of evolution by N / 4 steps. It turns out 9 squares with side N / 2. In turn, we will make 4 squares with a side N of them, and for each of them we will find the result of an evolution by N / 4 steps. The resulting 4 squares with a side of N / 2 will be combined into a square with a side of N - it will be the answer.

To implement the algorithm, we need to be able to do the following:
- Break the square into four squares;
- Find the result of the evolution of the square;
- Find the square consisting of four squares.
If you look for the result of evolution at the time of building the square, then it is enough to have a structure with 5 fields:
class Square {
internal Square LB, RB, LT, RT, Res;
} Then the algorithm of combining four squares into one can be written as:
Square Unite (Square a0, Square a1, Square a2, Square a3) {
Square res = FindInDictionary (a0, a1, a2, a3);
if (res! = null) return res;
// layer at T = N / 4
Square b1 = Unite (a0.RB, a1.LB, a0.RT, a1.LT) .Res;
Square b3 = Unite (a0.LT, a0.RT, a2.LB, a2.RB) .Res;
Square b4 = Unite (a0.RT, a1.LT, a2.RB, a3.LB) .Res;
Square b5 = Unite (a1.LT, a1.RT, a3.LB, a3.RB) .Res;
Square b7 = Unite (a2.RB, a3.LB, a2.RT, a3.LT) .Res;
// layer at T = N / 2
Square c0 = Unite (a0. Res, b1, b3, b4). Res;
Square c1 = Unite (b1, a1.Res, b4, b5) .Res;
Square c2 = Unite (b3, b4, a2.Res, b7) .Res;
Square c3 = Unite (b4, b5, b7, a3.Res) .Res;
return AddToDictionary (new Square () {LB = a0, RB = a1, LT = a1, RT = a3, Res = Unite (c0, c1, c2, c3)});
}
Actually, everything. Little things left:
Stop recursion. To do this, all 4 * 4 squares are entered into the dictionary and the results of their evolution are 1 step (in fact, only in this place the program requires knowledge of the rules of the game). For 2 * 2 squares, the evolution by half a step is not calculated, they are marked in some special way.
Double the number of evolutionary steps. In terms of the algorithm, this is the same as double the size of the square containing the original field. If we want to leave the square in the center, adding zeros to it, you can do this:
Square Expand (Square x) {
Square c0 = Unite (Zero, Zero, Zero, x.LB);
Square c1 = Unite (Zero, Zero, x.RB, Zero);
Square c2 = Unite (Zero, x.LT, Zero, Zero);
Square c3 = Unite (x.rt, zero, zero, zero);
return Unite (c0, c1, c2, c3);
}
Here Zero is a special square, all parts and the result of which is equal to itself.
And you can simply alternate the actions x = Unite (x, Zero, Zero, Zero) and x = Unite (Zero, Zero, Zero, x). The original square will be somewhere in the center.
Implement a dictionary. Here I did not find a beautiful solution: I need to search for an object by key, which is 80% of this object (and not only the remaining 20%, but also the object itself must be searched for). Fumbling with different types of collections, I waved my hand and entered Fortran: I described five integer arrays (LT, RT, LB, RB, Res) and said that the square is determined by an integer – index in these arrays. Indices from 0 to 15 are reserved for squares 2 * 2. The sixth array, twice as long, is used for hashing.
You also need to set the field and read the result - but this is a matter of technology. Although reading must be careful: if you run Expand more than 63 times, the length of the side of the field will no longer fit into 64 bits.
I tried the algorithm on such constructions:
"Garbage bin".

It moves at c / 2 speed, reserves a lot of garbage behind it and releases a pair of gliders every 240 steps. A trillion generations (more precisely, 2 ^ 40) were calculated in 0.73 seconds. Approximately 120000 squares fell into the dictionary (1500 for each doubling of time), the number of living cells per field was 600 billion.
A fragment of the resulting field looks like this:
(2001x2001, 82 KB)
"The battle of glider guns"
Two glider guns are located at a distance of 800 cells from each other, the flows released by them collide:
(T = 2048, 804x504, 11 KB)
Shortly after the collision, gliders fly out of a heap of debris, which first destroy one gun:
(T = 4096, 1098x1024, 30 Kb)
And then the second (after which the development quickly ends):
(T = 8192, 3146x3252, 190 Kb)
The counting time is 0.84 seconds, the number of elements in the dictionary is about 270,000.
"Random Filling"
Field 1024 * 1024 is randomly filled with cells with a density of 1/3. For the algorithm, this is the most difficult case: the configuration stabilizes slowly, and the squares do not begin to repeat immediately.
Here is an example of the development of one of the configurations:
(T = 0, 1024x1024, 300 Kb)
(T = 1024, 1724x1509, 147 Kb)
(T = 2048, 2492x2021, 177 Kb)
(T = 4096, 4028x3045, 300 Kb)
(T = 8192, 7100x5093, 711 Kb)
The counting time is 14 seconds, the number of elements in the dictionary is about 15 million, about 35,000 points remained on the field.
What is unusual about this algorithm? I would note the following:
- We almost without effort received a program capable of separating empty areas from active ones, tracking active areas and working out their interaction. If we wrote such an analysis directly, through a multitude of dynamic two-dimensional arrays, the program would be much more complicated.
- The algorithm not only calculates the state of the field in T steps - it remembers the entire development. From the result of his work, it is easy to extract the state through any interval T_k = 2 ^ k (how to get the state of the field in time that is not a power of two is a separate question). At the same time, the whole evolution turns out to be well-packed - again, without special efforts: 2 ^ 40 generations of the garbage bin were packed into 3 MB.
- Despite the fact that the dictionary is based on the original configuration, its contents are independent of this configuration. After we finish any calculation, we can use the same dictionary for the new configuration, and save a lot of time with luck (although I have not tried).
- Formally, the configurations on the plane are presented in the form of 4-trees. But to analyze the interaction between the extreme points of neighboring branches, we do not explicitly descend to these points, but only descend by 1-2 steps, after which we look for / build a tree suitable for solving our problem. However, there is nothing unusual here - only that we do not lose time because of the construction of new nodes, but rather, on the contrary.
- The algorithm never uses the actual size of "atomic" cells, or the number of their states. The lowest level to which recursion can go down is cells with 16 states, which we perceive as squares 2 * 2. The space-time at this level (for the algorithm) looks like a face-centered grid (a three-dimensional chessboard, from which only black cells were taken). The number 16 we came up with on the basis of Conway’s rules. It could be any in the algorithm, the main code does not depend on it
Source: https://habr.com/ru/post/136616/
All Articles