Multi-criteria selection of alternatives using fuzzy inference rules. Implementation in Java. Part 3/3: Example
Previous parts:
The example is taken from the book: Borisov, Krumberg, Fedorov - “Decision making based on fuzzy models. Examples of use ", 1990. Pp. 94-102
Condition. The management of the institute considers candidates for the vacant position at the faculty. The task is to use the method described above to identify the best of them. The discussion among the faculty members gave the following result:
d1: “If the candidate is an experienced researcher, has some work experience and experience in teaching technical disciplines, then he is satisfying (meets the requirements)”;
')
d2: “If, in addition to the above requirements, he can teach the theory of information systems, then he is more than satisfying”;
d3: “If he, in addition to the conditions of d2, has the ability to find a customer for high-tech products, then he is flawless”;
d4: “If it has everything that is contained in d3, except for the ability to teach the theory of information systems, then it is very satisfying”;
d5: “If the candidate is a very experienced researcher, has the ability to find a customer and a good teacher, but does not have production experience, he will nevertheless be satisfying”;
d6: "If he does not have the qualifications of a researcher or does not have a proven ability to teach, he is dissatisfied."
Analysis of six information fragments gives five criteria used in decision making:
X (1) - research skills;
X (2) - production experience
X (3) - experience in teaching technical subjects;
X (4) - Experience in Teaching Information Systems Theory
X (5) - the ability to find a customer.
We measure these variables on the base set U of candidates. Turning to six fragments, we get:

From rows A, B, C, D, E, a matrix is compiled, which is passed to the input class makeSkill method, which implements the Input interface. Its description is set forth below (see sentence transformation).
Fuzzy features
After this, fragments of knowledge take the form:
d (1): “If X = A, and B, and C, then Y = S”
d (2): "If X = A, and B, and C, and D, then Y = MS"
d (3): "If X = A, and B, and C, and D, and E, then Y = P”
d (4): “If X = A, and B, and C, and E, then Y = VS”
d (5): "If X is very A, and not B, and C, and E, then Y = S"
d (6): "If X = not A or not C, then Y = US"
In accordance with the above, the content of the functions in the implementation:
Transformation of statements
Using the rule to transform these statements, we get
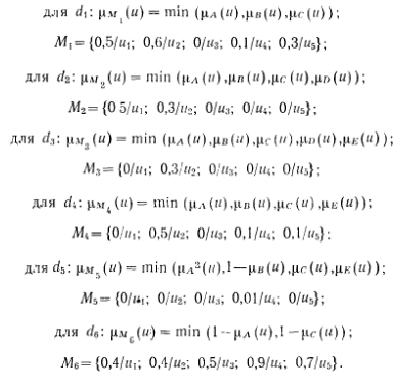
The Input class associating a rule with the required skills is:
In this way,
d (1): "If X = M (1), then Y = S"
d (2): "If X = M (2), then Y = MS"
d (3): "If X = M (3), then Y = P"
d (4): “If X = M (4), then Y = VS”
d (5): "If X = M (5), then Y = S"
d (6): "If X = M (6), then Y = US"

Calculations
Using the appropriate expression, we obtain the matrix D for each statement:

The result of the code:
D [1]:
0.5 0.60 0.70 0.80 0.9 1.0 1.0 1.0 1.0 1.0 1.0
0.4 0.50 0.60 0.70 0.8 0.9 1.0 1.0 1.0 1.0 1.0
0.5 0.60 0.70 0.80 0.9 1.0 1.0 1.0 1.0 1.0 1.0
0.9 1.00 1.00 1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.0
0.7 0.79 0.89 1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.0

D [2]:
0.5 0.53 0.58 0.66 0.75 0.85 0.96 1.0 1.0 1.0 1.0
0.7 0.73 0.78 0.86 0.95 1.00 1.00 1.0 1.0 1.0 1.0
0.5 0.53 0.58 0.66 0.75 0.85 0.96 1.0 1.0 1.0 1.0
0.9 0.93 0.98 1.00 1.00 1.00 1.00 1.0 1.0 1.0 1.0
0.7 0.73 0.78 0.86 0.95 1.00 1.00 1.0 1.0 1.0 1.0
Here the results do not agree, but the matlab and the calculator are on my side. Most likely, this is a miscalculation of the author.

D [3]:
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 1.0
0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 1.0
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 1.0
0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 1.0
0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 1.0
The same story is probably one of the functions in the calculations of the author was with an error.

D [4]:
0.5 0.51 0.54 0.59 0.66 0.75 0.86 0.99 1.0 1.0 1.0
0.5 0.51 0.54 0.59 0.66 0.75 0.86 0.99 1.0 1.0 1.0
0.5 0.51 0.54 0.59 0.66 0.75 0.86 0.99 1.0 1.0 1.0
0.9 0.91 0.94 0.99 1.00 1.00 1.00 1.00 1.0 1.0 1.0
0.9 0.91 0.94 0.99 1.00 1.00 1.00 1.00 1.0 1.0 1.0

D [5]:
0.50 0.6 0.7 0.8 0.9 1.0 1.0 1.0 1.0 1.0 1.0
1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
0.99 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0

D [6]:
1.0 1.0 1.0 1.0 1.0 1.0 1.00 1.00 0.90 0.8
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.00 1.00 1.00 0.9
1.0 1.0 1.0 1.0 1.0 1.0 1.00 1.00 1.00 1.0
1.0 1.0 1.0 1.0 1.0 1.0 0.99 0.89 0.79 0.7
1.0 1.0 1.0 1.0 1.0 1.0 1.00 1.00 1.00 1.0
The general functional solution D is found as the intersection of the fuzzy sets D (i):

D:
0.5 0.50 0.50 0.50 0.50 0.5 0.5 0.5 0.50 0.50 0.8
0.4 0.50 0.54 0.59 0.66 0.7 0.7 0.7 0.70 0.70 0.9
0.5 0.50 0.50 0.50 0.50 0.5 0.5 0.5 0.50 0.50 1.0
0.9 0.90 0.90 0.90 0.90 0.9 0.9 0.9 0.89 0.79 0.7
0.7 0.73 0.78 0.86 0.90 0.9 0.9 0.9 0.90 0.90 1.0
The possible reason for the discrepancy of the results described above, then the comparison with the book goes to demonstrate the general course of the decision, who was “more correct” - the question. The formulas are the same, but this implementation, matlab, calculator, is in my favor; The author of the textbook has an order of magnitude more experience, but the method of calculation is unknown - the only copy of the book found dates back to the 1990s and the same mistake cannot be ruled out.
Counting Point Estimates

My result:
Object # 1:
E: 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.8
X: 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.7 0.8 0.9 1.0
Point estimate: 0.6875

Object # 2:
E: 0.4 0.5 0.54 0.59 0.66 0.7 0.7 0.7 0.7 0.7 0.9
X: 0.0 0.1 0.20 0.30 0.40 0.5 0.6 0.7 0.8 0.9 1.0
Point estimate: 0.6561

Object # 3:
E: 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 1.0
X: 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.7 0.8 0.9 1.0
Point estimate: 0.7500

Object # 4:
E: 0.7 0.79 0.89 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9
X: 0.0 0.10 0.20 0.3 0.4 0.5 0.6 0.7 0.8 0.8 0.9 1.0
Point estimate: 0.4833

Object # 5:
E: 0.7 0.73 0.78 0.86 0.9 0.9 0.9 0.9 0.9 0.9 1.0
X: 0.0 0.10 0.20 0.30 0.4 0.5 0.6 0.7 0.8 0.9 1.0
Point estimate: 0.5757308868523388

Obviously, the third alternative is best (score 0.75).
In the book, the second candidate is recognized as the best candidate (before rounding his score was higher than that of the first).
Sources (project from NetBeans 6.9.1): ifolder.ru
pass: habrahabr.ru
Just in case: the .jar executable is in the \ dist \ folder
- Multi-criteria selection of alternatives using fuzzy inference rules. Part 1/3: Theory
- Multi-criteria selection of alternatives using fuzzy inference rules. Implementation in Java. Part 2/3: Basic Algorithm
The example is taken from the book: Borisov, Krumberg, Fedorov - “Decision making based on fuzzy models. Examples of use ", 1990. Pp. 94-102
Condition. The management of the institute considers candidates for the vacant position at the faculty. The task is to use the method described above to identify the best of them. The discussion among the faculty members gave the following result:
d1: “If the candidate is an experienced researcher, has some work experience and experience in teaching technical disciplines, then he is satisfying (meets the requirements)”;
')
d2: “If, in addition to the above requirements, he can teach the theory of information systems, then he is more than satisfying”;
d3: “If he, in addition to the conditions of d2, has the ability to find a customer for high-tech products, then he is flawless”;
d4: “If it has everything that is contained in d3, except for the ability to teach the theory of information systems, then it is very satisfying”;
d5: “If the candidate is a very experienced researcher, has the ability to find a customer and a good teacher, but does not have production experience, he will nevertheless be satisfying”;
d6: "If he does not have the qualifications of a researcher or does not have a proven ability to teach, he is dissatisfied."
Analysis of six information fragments gives five criteria used in decision making:
X (1) - research skills;
X (2) - production experience
X (3) - experience in teaching technical subjects;
X (4) - Experience in Teaching Information Systems Theory
X (5) - the ability to find a customer.
We measure these variables on the base set U of candidates. Turning to six fragments, we get:

From rows A, B, C, D, E, a matrix is compiled, which is passed to the input class makeSkill method, which implements the Input interface. Its description is set forth below (see sentence transformation).
Fuzzy features
After this, fragments of knowledge take the form:
d (1): “If X = A, and B, and C, then Y = S”
d (2): "If X = A, and B, and C, and D, then Y = MS"
d (3): "If X = A, and B, and C, and D, and E, then Y = P”
d (4): “If X = A, and B, and C, and E, then Y = VS”
d (5): "If X is very A, and not B, and C, and E, then Y = S"
d (6): "If X = not A or not C, then Y = US"
In accordance with the above, the content of the functions in the implementation:
package Function; import Support.Function; public class mMS extends Function { /*, */ public mMS(){} public double getY(double x) { return x*Math.sqrt(x); } } package Function; import Support.Function; public class mP extends Function{ /**/ public mP(){} public double getY(double x) { if (x==1) return 1; return 0; } } package Function; import Support.Function; public class mVS extends Function{ /* */ public mVS(){} public double getY(double x) { return x*x; } } package Function; import Support.Function; public class mS extends Function { /**/ public mS(){} public double getY(double x) { return x; } } package Function; import Support.Function; public class mUS extends Function{ /* */ public mUS(){} public double getY(double x) { return 1-x; } } Transformation of statements
Using the rule to transform these statements, we get
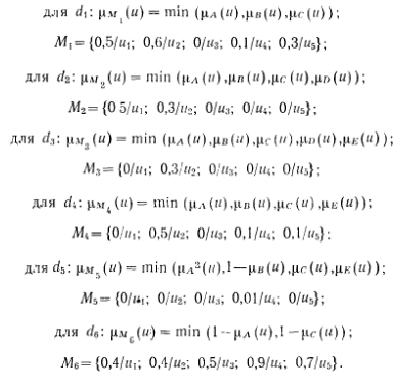
The Input class associating a rule with the required skills is:
package FLO_Engine; import Support.Function; import Support.Input; import Support.Rule; import Support.Skill; public class input extends Input{ private Skill A,B,C,D,E,A_M5,B_M5,A_M6,C_M6; public input(){ /* */ PARAMS_CNT = 5; FUNC_CNT = 6; } public void initFunc(Function[] func){ this.func = func; } private void makeSkill(double[][] arr){ /* ; , Function */ rl = new Rule[FUNC_CNT]; A = new Skill(arr[0]); B = new Skill(arr[1]); C = new Skill(arr[2]); D = new Skill(arr[3]); E = new Skill(arr[4]); double[][] u=arr; double[] a_m5 = (double[]) u[0].clone(); for (int i=0;i<u[0].length;i++) a_m5[i]*=a_m5[i]; /* */ A_M5 = new Skill(a_m5); double[] b_m5 = (double[]) u[1].clone(); for (int i=0;i<u[1].length;i++) b_m5[i]= 1 — b_m5[i]; /* */ B_M5 = new Skill(b_m5); double[] a_m6 = (double[]) u[0].clone(); for (int i=0;i<u[0].length;i++) a_m6[i] = 1 — a_m6[i]; /* */ A_M6 = new Skill(a_m6); double[] c_m6 = (double[]) u[2].clone(); for (int i=0;i<u[2].length;i++) c_m6[i] = 1 — c_m6[i]; /* */ C_M6 = new Skill(c_m6); } public Rule[] makeRules(double[][] arr) throws Exception{ makeSkill(arr); rl[0] = new Rule(new Skill[]{A,B,C} ,func[0]); // d1 rl[1] = new Rule(new Skill[]{A,B,C,D} ,func[1]); // d2 rl[2] = new Rule(new Skill[]{A,B,C,D,E} ,func[2]); // d3 rl[3] = new Rule(new Skill[]{A,B,C,E} ,func[3]); // d4 rl[4] = new Rule(new Skill[]{A_M5,B_M5,C,E} ,func[4]); // d5 rl[5] = new Rule(new Skill[]{A_M6,C_M6} ,func[5]); // d6 return rl; } } In this way,
d (1): "If X = M (1), then Y = S"
d (2): "If X = M (2), then Y = MS"
d (3): "If X = M (3), then Y = P"
d (4): “If X = M (4), then Y = VS”
d (5): "If X = M (5), then Y = S"
d (6): "If X = M (6), then Y = US"

Calculations
Using the appropriate expression, we obtain the matrix D for each statement:

The result of the code:
D [1]:
0.5 0.60 0.70 0.80 0.9 1.0 1.0 1.0 1.0 1.0 1.0
0.4 0.50 0.60 0.70 0.8 0.9 1.0 1.0 1.0 1.0 1.0
0.5 0.60 0.70 0.80 0.9 1.0 1.0 1.0 1.0 1.0 1.0
0.9 1.00 1.00 1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.0
0.7 0.79 0.89 1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.0

D [2]:
0.5 0.53 0.58 0.66 0.75 0.85 0.96 1.0 1.0 1.0 1.0
0.7 0.73 0.78 0.86 0.95 1.00 1.00 1.0 1.0 1.0 1.0
0.5 0.53 0.58 0.66 0.75 0.85 0.96 1.0 1.0 1.0 1.0
0.9 0.93 0.98 1.00 1.00 1.00 1.00 1.0 1.0 1.0 1.0
0.7 0.73 0.78 0.86 0.95 1.00 1.00 1.0 1.0 1.0 1.0
Here the results do not agree, but the matlab and the calculator are on my side. Most likely, this is a miscalculation of the author.

D [3]:
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 1.0
0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 1.0
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 1.0
0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 1.0
0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 1.0
The same story is probably one of the functions in the calculations of the author was with an error.

D [4]:
0.5 0.51 0.54 0.59 0.66 0.75 0.86 0.99 1.0 1.0 1.0
0.5 0.51 0.54 0.59 0.66 0.75 0.86 0.99 1.0 1.0 1.0
0.5 0.51 0.54 0.59 0.66 0.75 0.86 0.99 1.0 1.0 1.0
0.9 0.91 0.94 0.99 1.00 1.00 1.00 1.00 1.0 1.0 1.0
0.9 0.91 0.94 0.99 1.00 1.00 1.00 1.00 1.0 1.0 1.0

D [5]:
0.50 0.6 0.7 0.8 0.9 1.0 1.0 1.0 1.0 1.0 1.0
1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
0.99 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0

D [6]:
1.0 1.0 1.0 1.0 1.0 1.0 1.00 1.00 0.90 0.8
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.00 1.00 1.00 0.9
1.0 1.0 1.0 1.0 1.0 1.0 1.00 1.00 1.00 1.0
1.0 1.0 1.0 1.0 1.0 1.0 0.99 0.89 0.79 0.7
1.0 1.0 1.0 1.0 1.0 1.0 1.00 1.00 1.00 1.0
The general functional solution D is found as the intersection of the fuzzy sets D (i):

D:
0.5 0.50 0.50 0.50 0.50 0.5 0.5 0.5 0.50 0.50 0.8
0.4 0.50 0.54 0.59 0.66 0.7 0.7 0.7 0.70 0.70 0.9
0.5 0.50 0.50 0.50 0.50 0.5 0.5 0.5 0.50 0.50 1.0
0.9 0.90 0.90 0.90 0.90 0.9 0.9 0.9 0.89 0.79 0.7
0.7 0.73 0.78 0.86 0.90 0.9 0.9 0.9 0.90 0.90 1.0
The possible reason for the discrepancy of the results described above, then the comparison with the book goes to demonstrate the general course of the decision, who was “more correct” - the question. The formulas are the same, but this implementation, matlab, calculator, is in my favor; The author of the textbook has an order of magnitude more experience, but the method of calculation is unknown - the only copy of the book found dates back to the 1990s and the same mistake cannot be ruled out.
Counting Point Estimates

My result:
Object # 1:
E: 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.8
X: 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.7 0.8 0.9 1.0
Point estimate: 0.6875

Object # 2:
E: 0.4 0.5 0.54 0.59 0.66 0.7 0.7 0.7 0.7 0.7 0.9
X: 0.0 0.1 0.20 0.30 0.40 0.5 0.6 0.7 0.8 0.9 1.0
Point estimate: 0.6561

Object # 3:
E: 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 1.0
X: 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.7 0.8 0.9 1.0
Point estimate: 0.7500

Object # 4:
E: 0.7 0.79 0.89 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9
X: 0.0 0.10 0.20 0.3 0.4 0.5 0.6 0.7 0.8 0.8 0.9 1.0
Point estimate: 0.4833

Object # 5:
E: 0.7 0.73 0.78 0.86 0.9 0.9 0.9 0.9 0.9 0.9 1.0
X: 0.0 0.10 0.20 0.30 0.4 0.5 0.6 0.7 0.8 0.9 1.0
Point estimate: 0.5757308868523388

Obviously, the third alternative is best (score 0.75).
In the book, the second candidate is recognized as the best candidate (before rounding his score was higher than that of the first).
Sources (project from NetBeans 6.9.1): ifolder.ru
pass: habrahabr.ru
Just in case: the .jar executable is in the \ dist \ folder
Source: https://habr.com/ru/post/136227/
All Articles