3D Life - in search of gliders

Many people know the game “Life”, invented by J. Conway in 1970. One of the objects of this game, the glider (or glider), is even more widely known - a moving formation of 5 cells:

.
')
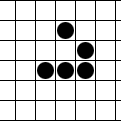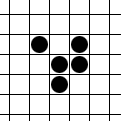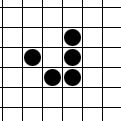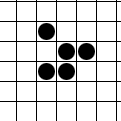In 1987, the first gliders were found in three-dimensional versions of "life" ( www.complex-systems.com/pdf/16-4-7.pdf ). Unfortunately, they occur very rarely from random configurations (unlike the two-dimensional version). I decided to look for the rules of the game in which there would be more gliders.

Let me remind the rules. There is some regular lattice. Each of its cells (cells) has a set of neighbors (in the case of a square grid on the plane, usually take 8 neighbors, and for a cubic grid in space - 26). Each cell can be either alive or dead. For each time step, dead cells, the number of living neighbors of which belongs to a certain set of B, come to life, and living cells, the number of living neighbors of which do not belong to a set, die. A pair of S / B determines the laws of development. For example, the classic Conway game has the rules S2,3 / B3 (or B3 / S2,3 - they write differently in different places, so the letters B and S should be left).

Depending on the rules, the development of cell configuration may be different. In some cases, a random configuration eventually dies out completely:



In others, it comes to a stable or periodic state:



Thirdly, the area with living cells occupies the whole space, and we see only an indiscriminate alternation of living and dead cells:



And finally, in the fourth type rules, compact stable structures exhibit an arbitrarily complex behavior. Finding such rules is the dream of any researcher who is not too lazy to do it, but it’s not at all easy. An example of such rules is the actual game of Conway. Are there others, I do not know.

How to search for gliders? The first thing that comes to mind is to take a certain range of rules. For example, only cells with 5 to 9 neighbors can be born, and survivors can have between 4 and 10 neighbors. This gives 4096 possible rules, and given that at least someone must be born - even less. Take the cube 200x200x200. Fill its central area with a size of 100x100x100 random cells with a certain density, leave the rest of the space empty. We're going through all the rules.

For each rule, we calculate several generations of the configuration - in order to reduce the influence of the initial chaos (I took 60, but this is with a margin). We look at how many living cells we have left and how much has changed in the last step.

If there are more than 100,000 cells left or more than 50,000 have changed - we say that we have a rule of the 3rd type, which is of no interest. Maybe the active area will occupy all the space, and maybe it will remain within the original cube - it is not very important, we are not going to look for stable structures in it (although it is possible that they will be there if you minimize the image with a suitable core).

If there are no changed cells, then we also discard the rule, it is of the 1st or 2nd type: we consider that if we have gliders, then at least a few pulsars should be obtained from any configuration.

In other cases, we calculate the evolution further, in portions of 60 generations. We check both previous conditions, and in addition, we check whether the configuration has returned to its previous state in 60 steps. If it returns, then development is over - but pulsars exist. Remember the rule for further research.

In addition, we check whether living cells have reached the cube border (for example, at a distance of 10). If so, then we have a big chance that a glider is found. Or something else interesting.

If the development has reached the 1200th generation and has not stopped for any of the above reasons, then the rule still remains on the list of suspicious ones, remember it.

Now we look through the list of “suspicious” rules, and begin to examine them manually.
The plan seemed good, and with it I found several new gliders. But I quickly discovered that the picture of development might look like this:



In general, evolution behaves as a rule of the second type, but if in some place the density turns out to be more critical, an active region arises there, which ultimately expands to the whole space. In Beys' work, such rules are immediately discarded as violating the condition of “the limited growth of random configurations”. I did not want to discard them, so I had to complicate the brute force algorithm.

Now for each rule I calculate not one, but four random configurations - with a density of living cells of 3%, 6%, 12% and 24% (the numbers are taken from the ceiling, but they seemed to me quite reasonable). Then I follow the above described algorithm, but I remember not only the rules, but also the density.

984 configurations out of 15872 passed the first stage of selection. It was too long to see them manually, so the next level of selection also went to the computer.

View the rules and density configurations. For each, we take 4 density values ​​close to the recorded one (for more fine-tuning), for each value we build two random fillings, and process them with the same algorithm as in the first stage. But this time we are only interested in gliders (configurations, whose living cells have reached the cube boundary), and, just in case, not stabilized configurations (calculated before generation 1200). You never know what's going on there?

For all configurations that have passed the second selection stage, we save the starting conditions (rules, density and starting value RND) for further study.

The total number of rules that have passed the second stage is 30. Some have recorded only one starting configuration, others have several dozen.

We start to look.

The first rule from which the popularization of three-dimensional "life" began was B5 / S4,5 ("it is remarkable that all the parameters are exactly 2 more than in the classical version"). Indeed, the program has found this rule and the glider. With a density of about 18%, the configuration stabilizes in about 100 generations, 450-500 living cells remain (0.05% density), the probability of a glider appearing is about 1/10 (that is, 1 per 10 million cells of volume).





The list had several more similar rules: B5 / S4,5,9; B5 / S4,5,10; B5.9 / S4,5,9; B5,9 / S4,5,10
But if in the second of these rules the glider looks the same as in B5 / S4,5, then in the first more often a different, lighter type appears:



In the last two rules, gliders are completely different. In B5.9 / S4,5,9 there are two of them (with periods 4 and 6): the first one is the same as in the previous picture, and the second one is:



And they do not always have a chance to survive



Maybe in an infinite space the glider would have managed to fly away from the active region, but in a closed universe there is no chance.

And in rule B5.9 / S4,5,10 there is a light glider with a period of 2:



But these rules are not the most popular in the list. Most places there are occupied by B6 / S5,7 and its "gain" (B6 / S5,6,7, etc.) If you look at the gliders arising in them, it becomes clear what's the matter:



If we take the configuration from Conway’s “life”, in which none of the empty cells have 6 neighbors (and 5 have live neighbors) and write it in “two layers”, then it will behave in exactly the same way in rule B6 / S5.7 as original. Therefore, in the space appear "blocks", "boxes", "flashers" and other simple shapes. Unfortunately, the glider gun will not survive there.
An example of development from the very beginning:



But, of course, in this universe there are other objects that have no analogues in 2D ...



This is just the beginning. With other rules come across other types of gliders, and many more interesting things. So to be continued ...