The solution of the inverse problem of analytic geometry. The theory of R-functions
Inspired by a recent post about the construction of various images using the Hubert curve. There will be some theory and some pictures.
The computer age spawned the theory of R-functions, functions with a “logical charge,” which arose at the junction of discrete and continuous analyzes, using the apparatus of Boolean algebra, which is inherently inherent in computers. On the basis of the theory of R-functions, the inverse problem of analytic geometry was solved, it became possible to build an equation of the boundary of a complex object as an elementary function, and, moreover, an equation that would have the necessary differential properties . VL Rvachev , using the constructive apparatus of the theory of R-functions, developed a unified approach to the problem of constructing coordinate sequences for basic variational and projection methods. To date, the R-function method has been applied to solve a large number of problems of electrodynamics, the mechanics of a deformable solid, the theory of plates and shells, hydrodynamics and magnetic hydrodynamics, thermal physics, etc.
Denote .
.
If you name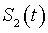 boolean sign
boolean sign  , then we can give such a definition of R-functions: function
, then we can give such a definition of R-functions: function 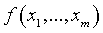 is called an R-function if the boolean sign of this function is equal to the boolean function of the Boolean characters of the arguments
is called an R-function if the boolean sign of this function is equal to the boolean function of the Boolean characters of the arguments  . Any Boolean function can be represented through
. Any Boolean function can be represented through  (in conjunctive and disjunctive normal forms). This fact means that the system is a complete system of Boolean functions (that is, the set of H-realizable functions (M (H)) is the set of all Boolean functions).
(in conjunctive and disjunctive normal forms). This fact means that the system is a complete system of Boolean functions (that is, the set of H-realizable functions (M (H)) is the set of all Boolean functions).
Consider the functions:
The functions of the first column are R-functions . Any continuous function of any number of arguments can be attributed to one of these columns. What attribute separates R-functions from non-R-functions, presented in the second column?
A person who does not have prior acquaintance with R-functions can hardly guess the “secret of R-functions”. Meanwhile, this feature is very simple: R-functions have the property that specifying the signs of the arguments uniquely determines the sign of the R-function . And this is their genius. For This property is obvious. In order to prove its fairness for
This property is obvious. In order to prove its fairness for  consider a right triangle with sides
consider a right triangle with sides 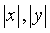 . If a
. If a 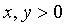 , then the modules can not write, and then the amount of the legs is more than the hypotenuse:
, then the modules can not write, and then the amount of the legs is more than the hypotenuse:  . If a
. If a 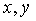 have different signs then
have different signs then  there is a difference between the legs, and then
there is a difference between the legs, and then 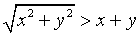 . If a
. If a  negative then all the more
negative then all the more 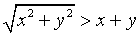 . Signs
. Signs 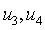 same as u
same as u 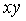 and sign
and sign  same as u
same as u  . It is obvious. Thus, for these functions, you can create a table of characters.
. It is obvious. Thus, for these functions, you can create a table of characters.
If in this table we replace “-” with “0”, and “+” with “1”, then we will get the tables of three Boolean functions. For example, functions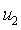 matching conjunction
matching conjunction 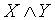 functions
functions  matches the boolean function
matches the boolean function  .
.
')
The most common and historically first is such a system of R-functions:

Let simple (support) areas be given.
 - vertical line between straight lines
- vertical line between straight lines 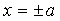 ,
,
 - horizontal stripe between straight lines
- horizontal stripe between straight lines 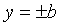 ,
,
 - vertical line between straight lines
- vertical line between straight lines  ,
,
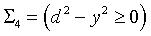 - horizontal stripe between straight lines
- horizontal stripe between straight lines 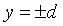 ,
,
a complex drawing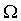 determined by the logical formula:
determined by the logical formula: 
It is easy to see that this drawing is a cruciform area shown in the figure, provided that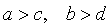 .
.
The result is:

The apparatus of R-functions will allow you to build the objects shown below, while we always know the exact (analytical) expression for each geometric object, and in fact we can not lose accuracy on the approximate description of the object's geometry.
And here is the program that can visualize and solve puzzles using R-functions
Source: Rvachev V.L. The theory of R-functions and some of its applications
A bit of theory
The computer age spawned the theory of R-functions, functions with a “logical charge,” which arose at the junction of discrete and continuous analyzes, using the apparatus of Boolean algebra, which is inherently inherent in computers. On the basis of the theory of R-functions, the inverse problem of analytic geometry was solved, it became possible to build an equation of the boundary of a complex object as an elementary function, and, moreover, an equation that would have the necessary differential properties . VL Rvachev , using the constructive apparatus of the theory of R-functions, developed a unified approach to the problem of constructing coordinate sequences for basic variational and projection methods. To date, the R-function method has been applied to solve a large number of problems of electrodynamics, the mechanics of a deformable solid, the theory of plates and shells, hydrodynamics and magnetic hydrodynamics, thermal physics, etc.
Definition of R-functions and basic systems of R-functions
Denote
 .
.If you name
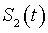 boolean sign
boolean sign 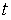 , then we can give such a definition of R-functions: function
, then we can give such a definition of R-functions: function 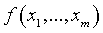 is called an R-function if the boolean sign of this function is equal to the boolean function of the Boolean characters of the arguments
is called an R-function if the boolean sign of this function is equal to the boolean function of the Boolean characters of the arguments  . Any Boolean function can be represented through
. Any Boolean function can be represented through  (in conjunctive and disjunctive normal forms). This fact means that the system is a complete system of Boolean functions (that is, the set of H-realizable functions (M (H)) is the set of all Boolean functions).
(in conjunctive and disjunctive normal forms). This fact means that the system is a complete system of Boolean functions (that is, the set of H-realizable functions (M (H)) is the set of all Boolean functions).Consider the functions:
 | 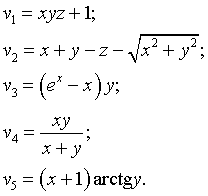 |
The functions of the first column are R-functions . Any continuous function of any number of arguments can be attributed to one of these columns. What attribute separates R-functions from non-R-functions, presented in the second column?
A person who does not have prior acquaintance with R-functions can hardly guess the “secret of R-functions”. Meanwhile, this feature is very simple: R-functions have the property that specifying the signs of the arguments uniquely determines the sign of the R-function . And this is their genius. For
 This property is obvious. In order to prove its fairness for
This property is obvious. In order to prove its fairness for 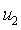 consider a right triangle with sides
consider a right triangle with sides 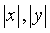 . If a
. If a 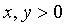 , then the modules can not write, and then the amount of the legs is more than the hypotenuse:
, then the modules can not write, and then the amount of the legs is more than the hypotenuse:  . If a
. If a 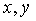 have different signs then
have different signs then  there is a difference between the legs, and then
there is a difference between the legs, and then 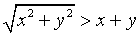 . If a
. If a  negative then all the more
negative then all the more 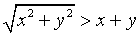 . Signs
. Signs 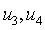 same as u
same as u 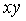 and sign
and sign  same as u
same as u  . It is obvious. Thus, for these functions, you can create a table of characters.
. It is obvious. Thus, for these functions, you can create a table of characters. | 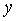 |  | 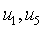 | 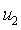 | 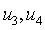 |
| - | - | - | - | - | + |
| - | - | + | + | - | + |
| - | + | - | + | - | - |
| - | + | + | - | - | - |
| + | - | - | + | - | - |
| + | - | + | - | - | - |
| + | + | - | - | + | + |
| + | + | + | + | + | + |
If in this table we replace “-” with “0”, and “+” with “1”, then we will get the tables of three Boolean functions. For example, functions
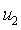 matching conjunction
matching conjunction 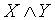 functions
functions  matches the boolean function
matches the boolean function  .
.')
The most common and historically first is such a system of R-functions:

Actually an example
Let simple (support) areas be given.
 - vertical line between straight lines
- vertical line between straight lines 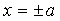 ,
, - horizontal stripe between straight lines
- horizontal stripe between straight lines 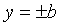 ,
, - vertical line between straight lines
- vertical line between straight lines  ,
,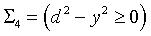 - horizontal stripe between straight lines
- horizontal stripe between straight lines 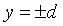 ,
,a complex drawing
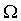 determined by the logical formula:
determined by the logical formula: 
It is easy to see that this drawing is a cruciform area shown in the figure, provided that
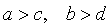 .
.The result is:

Some pictures
The apparatus of R-functions will allow you to build the objects shown below, while we always know the exact (analytical) expression for each geometric object, and in fact we can not lose accuracy on the approximate description of the object's geometry.
 |  |  |  |
And here is the program that can visualize and solve puzzles using R-functions
Source: Rvachev V.L. The theory of R-functions and some of its applications
Source: https://habr.com/ru/post/135549/
All Articles