Detection of elliptical particles on micrographs. New algorithm for finding ellipses in the image
I keep on messing around with my micrographs . Science does not stand still (since that article a year has passed without two months!), And now we need to recognize other objects:
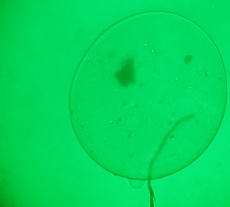
But here without any loosening: the accuracy should be quite high.
Specifically, this problem arose recently (approximately at the end of November), and was solved in my free time from study and work.
Achtung ! The article turned out quite large, a lot of pictures. But without excess mathematics.
We formulate the problem: to obtain parameters that fully characterize the outline of the figure shown in the picture .
')
Here I have an advantage: I know how these particles are made, and I also know that they are always of elliptical form, and this form tends to be ideal. A perfect ellipse is described by a second order curve equation:
Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0
Thus, the task is reduced to finding all these parameters. To find them, we need to know the coordinates of any six points that are known to lie on the ellipse (number of points = number of unknowns in the complete second-order equation above): then we can find all the parameters of the ellipse we need ( how to approximate six points with an ellipse read below, we are now solving another problem ). Actually, I immediately wrote a program where the user could poke six points with the mouse and the program gave out the area of the ellipse. It was written quickly, and it was with her help that I defended a term paper a week ago.
But how to select points automatically? Very simple: remember the sudoku decision article ? There the author uses an excellent algorithm for finding the singular points of the image (read the boundaries on the image).
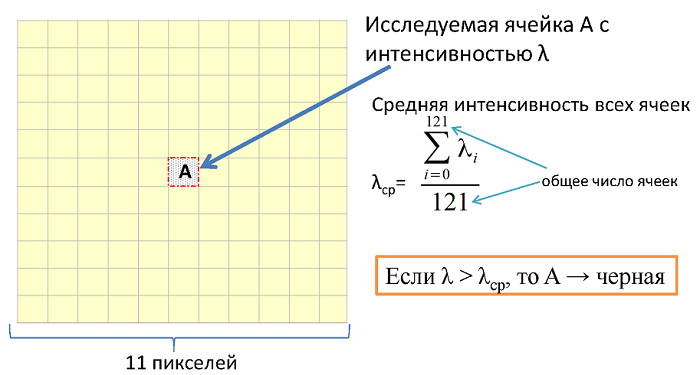
In short, what is its essence: to find the borders, we do not set one intensity border (which ranges from 0 to 255), with respect to which the pixels are repainted either white or black (if the intensity is less than a given border, the pixel is black, otherwise white). This approach is used in the Ots method, and there is nothing good in it except for the speed of execution. Very focused algorithm. Instead, it is better to use the "floating" border of intensity. A region of a known size is selected around the studied pixel (I used a region of 11x11 pixels). If its intensity is less than the average intensity of all pixels in the area, then it is the background, and it is painted over with white. If its intensity is greater, then it is painted over with black. A short diagram is shown in the figure below:
The result of this algorithm is almost satisfied. Here is about the result we get, following this algorithm:

Seeing this, it was immediately decided to “overstate” the value of the average intensity. Artificially raising this value by 15 units, I came to the following result:

And this result gave me a little more than full. Because there is practically nothing on it except the outline of my ellipse. This in itself is excellent!
But we need to move on. Remember why we started all this? We need to determine the parameters of the complete equation of the second order curve by the six points lying on the ellipse. At the moment we are still far from the final decision, because we have found only an array of points (black dots) that can claim the ones we need. However, not all points will suit us ... Why exactly, I decided to show with a picture:
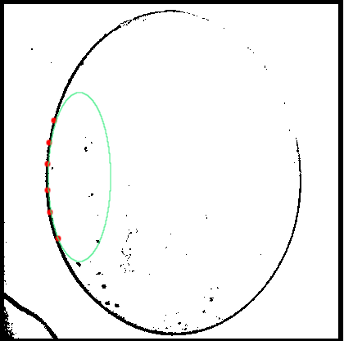
If the points are too close to each other, then at least six ellipses can be drawn through the given six points with the same confidence. Therefore, the selected six points should lie as far as possible from each other. Plus, obviously lying on an ellipse.
There was something to think about, and I really hung on for a week. However, his holiness, the Math.Rand () function saved me.
It was decided to remove random six points from the array, and build an ellipse on them. And so many, many times (empirically for an image of 700x700 pixels in size - two thousand iterations are enough)
The result met all my expectations: I did it. A function that converts six points into an ellipse (its algorithm is given just below) returned the coordinates of the center of the ellipse, the length of its two axes, and its angle of rotation relative to the axes of the coordinates. For clarity, I decided to draw the schema again:

From the data obtained, it was possible to construct the dependence x = f (y), where (x, y) are the coordinates of the center of the ellipse; and the dependence R 1 = f (R 2 ) - where R 1 and R 2 are the lengths of the axes of the ellipse. The point - at which the coordinates obtained are most often encountered - is our desired point (coordinate of coordinates, sorry for the tautology).
To make it clearer, I will quote a fragment of such a “sputtering” of the resulting array of points on a plane.
Spray the coordinates of the center of the ellipse:
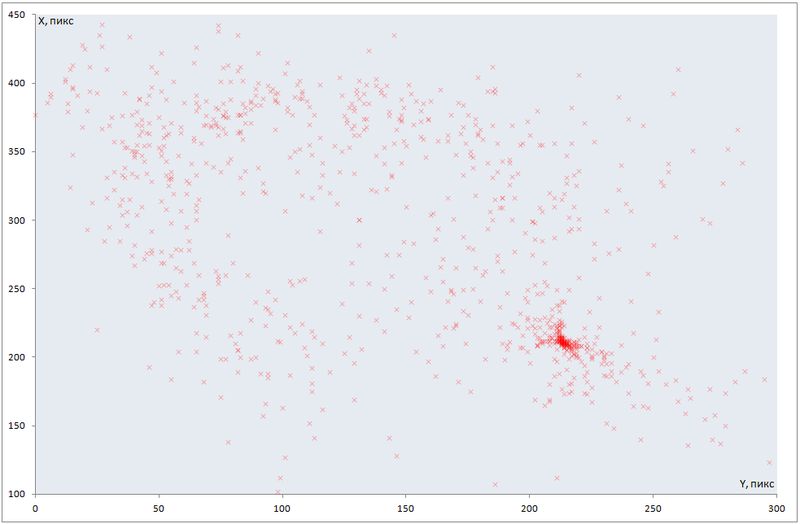
As can be seen with the naked eye - the maximum is approximately at X = 210, Y = 220; These points are the coordinates of the center of our image.
How to search for a maximum of points aggregation? Oooh ... I asked a question here (on Habré) - one person (let's not poke a finger at Monnoroch ) advised me of this, that the rays of hatred in his direction. But there were cool answers, including in a personal, thanks to everyone who responded! However, I still went my own way.
I took and created an empty array counter [] [], the dimension as the original image. And he began to sort through the array of points (x, y) obtained as a result of two thousand iterations. If the field is empty, then naturally I did not do anything. However, as soon as there is a point, then, firstly, we do counter [x] [y] = counter [x] [y] +2, and secondly, we also increase the counter for all neighbors. Forgive me for these schemes, but here's another one :)
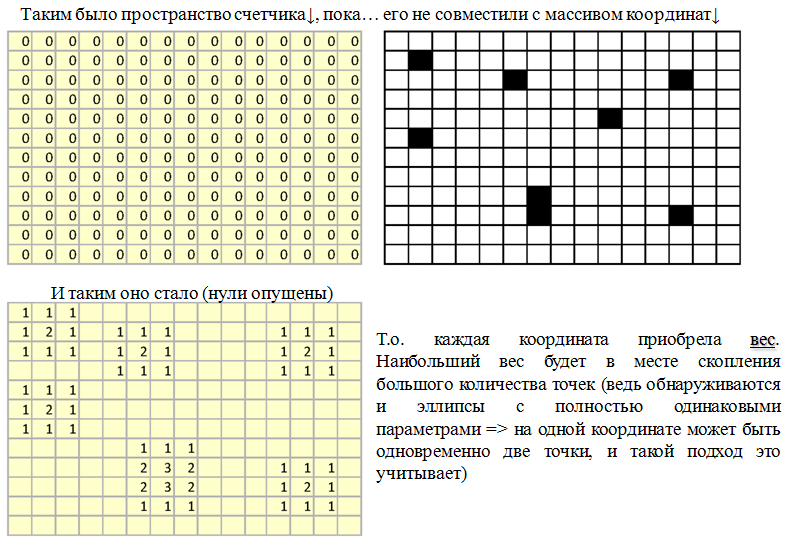
An absolutely identical picture and in the case of enumerating the resulting array of the lengths of the axes of the ellipse, in order not to overload the article, I will not give pictures for them. Believe me - absolutely the same thing.
Well that's all. The maxima are found, which means the coordinates, the lengths of the axes and the angle of rotation are known. Everything! :)
The result of the algorithm on the very first picture from the article:

PS Separately, thank you very much to the habrayuzer ruedj , who for so simply gave me his two-volume book (2011!) To Horstmann, and I finally learned to more or less properly communicate with multithreading. The entire algorithm on the image of 700x700 pixels on the core i3-2100 (one of the weakest models in the Sandy Bridge lineup) takes ~ 1000ms.

But here without any loosening: the accuracy should be quite high.
Specifically, this problem arose recently (approximately at the end of November), and was solved in my free time from study and work.
Achtung ! The article turned out quite large, a lot of pictures. But without excess mathematics.
We formulate the problem: to obtain parameters that fully characterize the outline of the figure shown in the picture .
')
Here I have an advantage: I know how these particles are made, and I also know that they are always of elliptical form, and this form tends to be ideal. A perfect ellipse is described by a second order curve equation:
Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0
Thus, the task is reduced to finding all these parameters. To find them, we need to know the coordinates of any six points that are known to lie on the ellipse (number of points = number of unknowns in the complete second-order equation above): then we can find all the parameters of the ellipse we need ( how to approximate six points with an ellipse read below, we are now solving another problem ). Actually, I immediately wrote a program where the user could poke six points with the mouse and the program gave out the area of the ellipse. It was written quickly, and it was with her help that I defended a term paper a week ago.
But how to select points automatically? Very simple: remember the sudoku decision article ? There the author uses an excellent algorithm for finding the singular points of the image (read the boundaries on the image).
In short, what is its essence: to find the borders, we do not set one intensity border (which ranges from 0 to 255), with respect to which the pixels are repainted either white or black (if the intensity is less than a given border, the pixel is black, otherwise white). This approach is used in the Ots method, and there is nothing good in it except for the speed of execution. Very focused algorithm. Instead, it is better to use the "floating" border of intensity. A region of a known size is selected around the studied pixel (I used a region of 11x11 pixels). If its intensity is less than the average intensity of all pixels in the area, then it is the background, and it is painted over with white. If its intensity is greater, then it is painted over with black. A short diagram is shown in the figure below:

The result of this algorithm is almost satisfied. Here is about the result we get, following this algorithm:

Seeing this, it was immediately decided to “overstate” the value of the average intensity. Artificially raising this value by 15 units, I came to the following result:

And this result gave me a little more than full. Because there is practically nothing on it except the outline of my ellipse. This in itself is excellent!
But we need to move on. Remember why we started all this? We need to determine the parameters of the complete equation of the second order curve by the six points lying on the ellipse. At the moment we are still far from the final decision, because we have found only an array of points (black dots) that can claim the ones we need. However, not all points will suit us ... Why exactly, I decided to show with a picture:

If the points are too close to each other, then at least six ellipses can be drawn through the given six points with the same confidence. Therefore, the selected six points should lie as far as possible from each other. Plus, obviously lying on an ellipse.
There was something to think about, and I really hung on for a week. However, his holiness, the Math.Rand () function saved me.
It was decided to remove random six points from the array, and build an ellipse on them. And so many, many times (empirically for an image of 700x700 pixels in size - two thousand iterations are enough)
The result met all my expectations: I did it. A function that converts six points into an ellipse (its algorithm is given just below) returned the coordinates of the center of the ellipse, the length of its two axes, and its angle of rotation relative to the axes of the coordinates. For clarity, I decided to draw the schema again:

From the data obtained, it was possible to construct the dependence x = f (y), where (x, y) are the coordinates of the center of the ellipse; and the dependence R 1 = f (R 2 ) - where R 1 and R 2 are the lengths of the axes of the ellipse. The point - at which the coordinates obtained are most often encountered - is our desired point (coordinate of coordinates, sorry for the tautology).
To make it clearer, I will quote a fragment of such a “sputtering” of the resulting array of points on a plane.
Spray the coordinates of the center of the ellipse:

As can be seen with the naked eye - the maximum is approximately at X = 210, Y = 220; These points are the coordinates of the center of our image.
How to search for a maximum of points aggregation? Oooh ... I asked a question here (on Habré) - one person (let's not poke a finger at Monnoroch ) advised me of this, that the rays of hatred in his direction. But there were cool answers, including in a personal, thanks to everyone who responded! However, I still went my own way.
I took and created an empty array counter [] [], the dimension as the original image. And he began to sort through the array of points (x, y) obtained as a result of two thousand iterations. If the field is empty, then naturally I did not do anything. However, as soon as there is a point, then, firstly, we do counter [x] [y] = counter [x] [y] +2, and secondly, we also increase the counter for all neighbors. Forgive me for these schemes, but here's another one :)

An absolutely identical picture and in the case of enumerating the resulting array of the lengths of the axes of the ellipse, in order not to overload the article, I will not give pictures for them. Believe me - absolutely the same thing.
Well that's all. The maxima are found, which means the coordinates, the lengths of the axes and the angle of rotation are known. Everything! :)
The result of the algorithm on the very first picture from the article:

PS Separately, thank you very much to the habrayuzer ruedj , who for so simply gave me his two-volume book (2011!) To Horstmann, and I finally learned to more or less properly communicate with multithreading. The entire algorithm on the image of 700x700 pixels on the core i3-2100 (one of the weakest models in the Sandy Bridge lineup) takes ~ 1000ms.
Mathematical part
Finding the parameters of the complete equation of the curve of the second order in six points. Tell me please, is it necessary to describe it here? I would not say that it is very difficult there (just to write for a long time).Source: https://habr.com/ru/post/135332/
All Articles