Heaps. Part 1. The Binomial Heap
Hello, Habrosoobschestvo!
On Habré there is a description of a set of interesting data structures, such as trees of segments, ducha, etc. If you are interested in complex data structures, then welcome under the cat! In my series of articles I will consider different types of heaps and how they are put into practice:
1) Binomial heap
2) Left heap
3) Fibonacci heap
4) Application of these data structures in practice
Formulation of the problem:
To build a data structure in which many of our objects will be stored (different depending on the task), each object will have a key field, according to which we can quickly find the minimum element. The following operations must be possible for this structure:
')
Many are familiar with the simplest ways to implement this structure, such as an array :) and a binary heap. I will not dwell on them in detail because of their simplicity and general knowledge.
As is known, for a binary heap, the asymptotics of the above operations are as follows:
I will not describe the algorithm of the binary heap, since it has been repeatedly described everywhere, including on Habré. For those who are not familiar with the binary heap, I would recommend before reading further to become familiar with it.
Next, we consider a more interesting data structure called the binomial heap .
Binomial heap
A binomial heap is a set of binomial trees with some limitations. We will introduce them later.
A binomial tree is a tree that is specified recursively:
B i is B i - 1 , in which the tree B i - 1 was made the left son of the root.
B 0 is just a vertex.
Examples for B 0 , B 2 , B 3 :
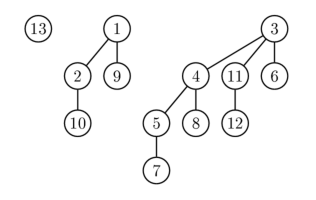
The binomial tree (B k ) has a number of interesting properties :
T.1. 2 k vertices
T.2. Tree height k
T.3. C i k vertices of depth i (which is why they are called binomial: C i k is the binomial coefficient).
T.4. The children of the root are B, B k - 2 , ..., B 0 - in that order.
T.5. The maximum height of the vertex in the binomial tree O (log N)
The properties are proved by induction. I suggest that readers themselves carry out the evidence for a better understanding of the trees.
So, now back to the binomial heaps . A binomial heap is a multitude of binomial trees, with the following limitations:
1) In each of the binomial trees, the heap property is preserved.
2) No two trees are the same size.
3) The trees are ordered by size.
Let's talk about how the binomial heap will be stored in the program. We will use the “left son - right brother” method. We will store the root list (
Immediately note:
Property H.1:
The length of
For the proof, it suffices to note that due to T.1, the presence of the tree B k in the binary notation.
Let us proceed to the description of operations that can be performed with the binomial heaps:
Make
Task : create an empty heap.
Algorithm : create an empty
Difficulty : obviously, the running time is O (1).
Merge
Task : merge 2 heaps into 1.
Algorithm : first combine the root lists of heaps into 1 root list, maintaining ordering by degree. The algorithm is similar to merging 2 arrays in mergeSort:
We keep at the pointer to the beginning of the lists and write the minimum of them in the resulting list, the one from which we have just written down is shifted to the next. Then we go from the beginning to the end of the newly obtained root list and merge trees of the same size into 1. There may be cases:
1) Only 2 trees of the same size. Then combine them.
2) 3 trees of the same size. Combine the last 2.
When combining two trees, you only need to look at the root of which one is the smaller key and make the other tree the left son of the root of this tree.
An example of what happens after merging two heaps:
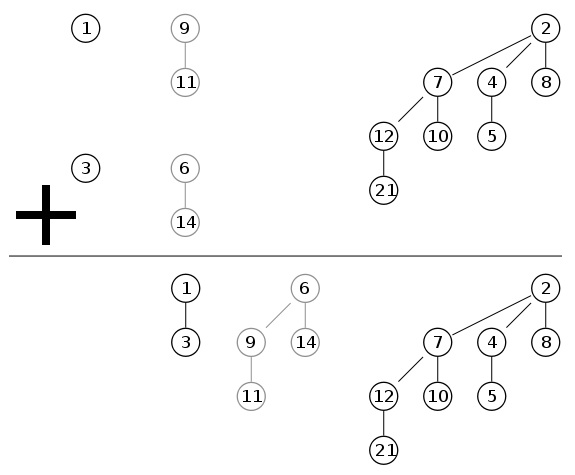
Complexity : Operating time O (
In one pass (O (log N)) we get the combined binomial tree. We get that the total complexity is O (log N).
Insert
Task : insert a new item into the heap.
Algorithm : Create a bunch of one element and combine with our bunch.
Complexity : O (1) + O (log (N)) = O (log (N)).
Minimum
Task : find the minimum in the heap.
Algorithm : obviously, the minimum is in the root list, that is, to find it you need to go through the root list.
Complexity : O (
ExtractMin
Task : remove the minimum element.
Algorithm : we find it using
Difficulty : since each operation in extracting the minimum works in O (log N): O (log N) + O (log N) + O (log N) = O (log N)
Decrease
Objective : reduce the value of data at this vertex.
Algorithm : decrement the value at the vertex. Then the heap property will probably be violated for our top and its ancestor, then we swap them. We continue the process until our peak “pops up” to its place. The algorithm also works like a binary one.
Difficulty : In the worst case, our vertex will pop up to the root, that is, we will perform O (log N) actions (the vertex at each step “pops up” a level higher, and the height of the binomial tree in T.5 O (log N))
Delete
Task : delete an arbitrary element.
Algorithm : first, using
Complexity : O (log N) + O (log N) = O (log N)
Conclusion
We looked at the binomial heap data structure and proved its asymptotics.
In the next article based on the binomial heap, we will construct a slightly more complex data structure, namely the Fibonacci heap.
You can play around with binomial heaps on rain.ifmo.ru/cat/view.php/vis/heaps/binomial-2001
You can read in more detail in T. Kormen "Algorithms: construction and analysis.".
Thank you all for your attention, and see you soon!
On Habré there is a description of a set of interesting data structures, such as trees of segments, ducha, etc. If you are interested in complex data structures, then welcome under the cat! In my series of articles I will consider different types of heaps and how they are put into practice:
1) Binomial heap
2) Left heap
3) Fibonacci heap
4) Application of these data structures in practice
Formulation of the problem:
To build a data structure in which many of our objects will be stored (different depending on the task), each object will have a key field, according to which we can quickly find the minimum element. The following operations must be possible for this structure:
Make - creating a new empty heap,Insert - insert a new item in the heap,Minimum - the minimum keyExtractMin - minimum extraction,Merge - the merger of 2 heaps,Decrease - key reduction,Delete - delete an object.')
Many are familiar with the simplest ways to implement this structure, such as an array :) and a binary heap. I will not dwell on them in detail because of their simplicity and general knowledge.
As is known, for a binary heap, the asymptotics of the above operations are as follows:
Make - O (1)Merge - O (N)Insert - O (log N) - where N is the number of elements in the heap.Minimum - O (1)ExtractMin - O (log N)Decrease - O (log N)Delete - O (log N)I will not describe the algorithm of the binary heap, since it has been repeatedly described everywhere, including on Habré. For those who are not familiar with the binary heap, I would recommend before reading further to become familiar with it.
Next, we consider a more interesting data structure called the binomial heap .
Binomial heap
A binomial heap is a set of binomial trees with some limitations. We will introduce them later.
A binomial tree is a tree that is specified recursively:
B i is B i - 1 , in which the tree B i - 1 was made the left son of the root.
B 0 is just a vertex.
Examples for B 0 , B 2 , B 3 :

The binomial tree (B k ) has a number of interesting properties :
T.1. 2 k vertices
T.2. Tree height k
T.3. C i k vertices of depth i (which is why they are called binomial: C i k is the binomial coefficient).
T.4. The children of the root are B, B k - 2 , ..., B 0 - in that order.
T.5. The maximum height of the vertex in the binomial tree O (log N)
The properties are proved by induction. I suggest that readers themselves carry out the evidence for a better understanding of the trees.
So, now back to the binomial heaps . A binomial heap is a multitude of binomial trees, with the following limitations:
1) In each of the binomial trees, the heap property is preserved.
2) No two trees are the same size.
3) The trees are ordered by size.
Let's talk about how the binomial heap will be stored in the program. We will use the “left son - right brother” method. We will store the root list (
root_list , its length is root_list.length ), which will contain the roots of binomial trees, in ascending order of height. Each vertex will have the following fields:data - data that is stored at the top (using them we find the minimum)right - right brotherchild - left sondegree - the degree of the vertex (obviously, the trees in the binomial heap are ordered by this field)Immediately note:
Property H.1:
The length of
root_list.length = O (log N), where N is the number of elements in the heap.For the proof, it suffices to note that due to T.1, the presence of the tree B k in the binary notation.
Let us proceed to the description of operations that can be performed with the binomial heaps:
Make
Task : create an empty heap.
Algorithm : create an empty
root_list .Difficulty : obviously, the running time is O (1).
Merge
Task : merge 2 heaps into 1.
Algorithm : first combine the root lists of heaps into 1 root list, maintaining ordering by degree. The algorithm is similar to merging 2 arrays in mergeSort:
We keep at the pointer to the beginning of the lists and write the minimum of them in the resulting list, the one from which we have just written down is shifted to the next. Then we go from the beginning to the end of the newly obtained root list and merge trees of the same size into 1. There may be cases:
1) Only 2 trees of the same size. Then combine them.
2) 3 trees of the same size. Combine the last 2.
When combining two trees, you only need to look at the root of which one is the smaller key and make the other tree the left son of the root of this tree.
An example of what happens after merging two heaps:

Complexity : Operating time O (
root_list1.length ) + O ( root_list2.length ) = (by property H.1) = O (log N).In one pass (O (log N)) we get the combined binomial tree. We get that the total complexity is O (log N).
Insert
Task : insert a new item into the heap.
Algorithm : Create a bunch of one element and combine with our bunch.
Complexity : O (1) + O (log (N)) = O (log (N)).
Minimum
Task : find the minimum in the heap.
Algorithm : obviously, the minimum is in the root list, that is, to find it you need to go through the root list.
Complexity : O (
root_list.length ) = O (log (N)).ExtractMin
Task : remove the minimum element.
Algorithm : we find it using
Minimum . Remove it from the root list. From the inverted list of his children, we root_list for a new heap (H 1 ) and merge the original heap with H 1 .Difficulty : since each operation in extracting the minimum works in O (log N): O (log N) + O (log N) + O (log N) = O (log N)
Decrease
Objective : reduce the value of data at this vertex.
Algorithm : decrement the value at the vertex. Then the heap property will probably be violated for our top and its ancestor, then we swap them. We continue the process until our peak “pops up” to its place. The algorithm also works like a binary one.
Difficulty : In the worst case, our vertex will pop up to the root, that is, we will perform O (log N) actions (the vertex at each step “pops up” a level higher, and the height of the binomial tree in T.5 O (log N))
Delete
Task : delete an arbitrary element.
Algorithm : first, using
Decrease reduce the value at the vertex to the minimum possible. And then delete the minimum in the heap ( ExtractMin ).Complexity : O (log N) + O (log N) = O (log N)
Conclusion
We looked at the binomial heap data structure and proved its asymptotics.
In the next article based on the binomial heap, we will construct a slightly more complex data structure, namely the Fibonacci heap.
You can play around with binomial heaps on rain.ifmo.ru/cat/view.php/vis/heaps/binomial-2001
You can read in more detail in T. Kormen "Algorithms: construction and analysis.".
Thank you all for your attention, and see you soon!
Source: https://habr.com/ru/post/135232/
All Articles