Hyperburg - a three-dimensional version of the game "Carcassonne"
Recently, at one of the forums devoted to multidimensional spaces, the question was asked: “And which games are implemented in non-trivial spaces, in particular, is there a realization of the game Carcassonne on the Lobachevsky plane?” I found the question interesting, especially since I never heard of.
And in vain! The game was simple enough to try to adapt it to different spaces. This is a board game. Players take turns putting cards on the table with fragments of a map of the area, trying to fold a coherent map. During the game, players can capture some elements of the field, and get points for the completed elements.
It is clear that the scope for generalizations towards non-trivial geometry is enormous. It is possible to develop instead of square cards triangular or hexagonal. You can stack square cards on the surface of the cube (8 special points will appear in which 3 and not 4 cards converge, but this is not very important). You can draw on the Lobachevsky plane a square grid, at each vertex of which 5 (or 6, or infinitely many) squares converge. And you can replace square cells with cubic ones and build a map in space.
')
I chose the last option. It was very interesting to see how the terrain map would look on a four-dimensional planet.
To begin with, it was necessary to decide which version of the game I would adapt: there are several different basic sets of cells and rules that also have extensions with additional elements and objects. The choice fell on the option "Discovery" (aka "New World", aka "New Earths"). There the land is divided into three areas (seas, mountains, plains), and for completed (and even unfinished) objects you can get points.
The first estimates showed that the three types of regions will be small: on average, the cube will have two faces of each color, and one can expect infinite growth of connected regions. Therefore, I immediately added a fourth type (desert) and set about implementing it.
Alas ... after only a few dozen tiles laid out, it became clear that it would not be possible to sort out the resulting map. The surface turned out to be too ragged, the translucent borders between areas of different colors were mixed, and it was impossible to understand how far this or that area stretches in any way:

Later I found a couple of ways giving a chance to make this option more or less understandable, so maybe I’ll come back to it. But so far it was necessary to look for something that allows you to make an interface that is clear and suitable for the game. And the following rules of simplicity were in the basic version of the game.
In the basic version there are four elements of topography: cities, roads, monasteries, and fields, which occupy the rest of the territory. Players in the process of the game can occupy roads (areas limited by ends or intersections), cities (areas limited by walls), monasteries (individual cells) and fields. For completed objects (except for fields) points are awarded (objects are released at the same time), and fields are evaluated only at the end of the game.
It is clear that in the three-dimensional case, the idea of a field, as an element of topography, does not work: roads do not divide the earth into parts, and in most cases the entire map turns out to be one large field interspersed with cities. To keep the interest, I added another similar pair to the cities and roads - the sea and the river. With a slightly different scoring: if a city is estimated by area, then the sea is based on the number of ports (cells where rivers flow into it and sections bordering cities), and in rivers, unlike roads, intersections are not the boundaries of the section. But these are all cosmetic edits. The first question is what the playing field will look like and what game cards will be.
For the game, it is necessary that the fragments of objects on the new cells continue unfinished objects that are already on the field. So, the edges of the cells should provide convenient opportunities for their joining. The easiest way to achieve this is to make the relief on the facets symmetrical — so that any two cells with faces of the same type can join along these faces in any of four possible ways. The selected game elements (plain, river, sea, road, city) provide such an opportunity: it is enough that the city and the sea can occupy the edges only as a whole, and the roads and rivers pass through the centers of the faces. If such a relief detail as canyons (two-dimensional surfaces that divide space into parts) were added, then this method would not work - we would have to take into account the mutual orientation of the cells relative to the axis passing through their centers. But in the current version of the game there are no canyons.
I divided the cell into 7 zones: 6 correspond to the faces and have the shape of truncated square pyramids, and the seventh - in the center, has the shape of a cube. External zones can be in one of 5 states (all but the monasteries), internal - in one of six. The geometry and topographic properties of a cell are completely determined by the states of its zones: two sections of the sea or a city belonging to adjacent faces are adjacent, if exactly two faces of the cell (and adjacent) are in the “road” state, then the road connects the centers of these faces (otherwise connects the face with the central zone). And there are a few limitations. For example, if a cell contains three or more roads, then the central zone should be a “city” (and play the role of an intersection).
I was afraid to list all possible cells, and I chose random generation: first, the state of all faces is determined by the cell (with certain probabilities: plain - with 1/2 probability, river and road - by 1/6, sea and city - by 1/12) , then the possible states of the central cell are determined. If a monastery is possible in the center, it is placed with a probability of 1/8, and if this does not happen, the state is chosen equiprobably from all possible. After that, the cell is offered for play. (Later, I considered that the number of different cells is about 750, so you can generate and include in the program a complete list of them, at the same time providing each with some probability of occurrence)
The starting cell looks like this:

It has fragments of the city, the river and the road. The cell is placed on the field, and the next cell is displayed in a separate window. For the move, you need to rotate the cage and the field so that the edge of the field to which we want to attach the cage was front, and the edge of the cage with which we want to attach it, looked towards it:

Use the left mouse button to rotate the cell and the field, and the right button to rotate the camera. To zoom in / out - Ctrl + left button.
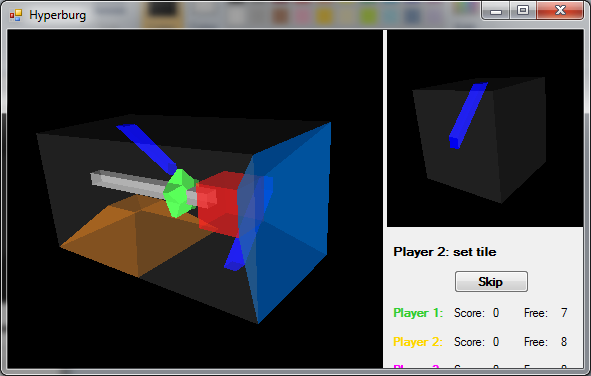
After choosing the correct orientation, just click on the center of the edge of the field on which you want to put a cage, and if a move is possible, then it is done. After that, the player is offered to put one of his chips (if there are free - only 8 of them) on some part of the cell. Possible areas are represented by blue balls:

The player can click on one of the balls or click the "Skip" button (if he does not want to put a chip). The selected ball turns into an asterisk of color corresponding to this player, and the turn turns to the next one.
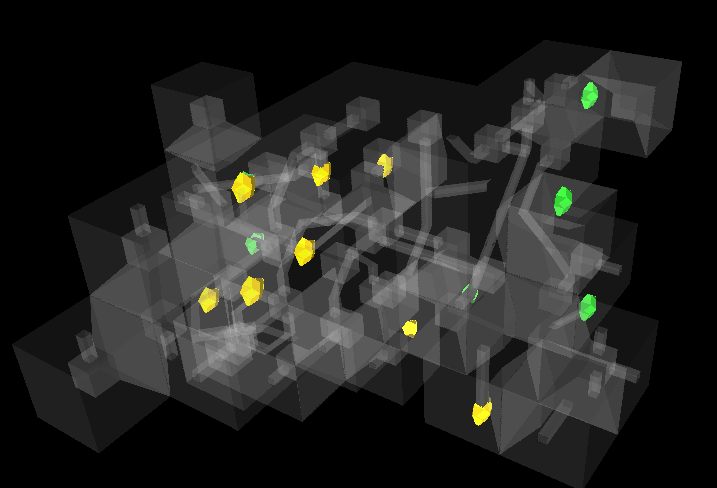
After a few moves, it becomes difficult to navigate the situation on the field:

To make life easier for players, there are several additional visualization modes. In order to analyze the outer edges of the cells on the field (and understand where you can walk), the outer edges of the field are made less transparent:

To better analyze the shape of individual objects, you can reduce their transparency and increase the transparency of the outer edges of the plain:

And finally, in order to more reliably determine the color of the chips on the field (for example, if the chip is in the sea or in the city), and just to see the position of all the chips, there is a mode in which all objects become white and almost transparent:
Before starting the game, you can select the number of players (from 2 to 5) and the duration of the game (the number of moves is from 20 to 10,000). After selecting them, click the New Game button.
Read more detailed rules (in English) can be
on this page . The executable code can be downloaded from here , and the source code from here . The program is written in C # using the Open Toolkit library. Requires Windows with .NET 2.0 to work
And in vain! The game was simple enough to try to adapt it to different spaces. This is a board game. Players take turns putting cards on the table with fragments of a map of the area, trying to fold a coherent map. During the game, players can capture some elements of the field, and get points for the completed elements.
It is clear that the scope for generalizations towards non-trivial geometry is enormous. It is possible to develop instead of square cards triangular or hexagonal. You can stack square cards on the surface of the cube (8 special points will appear in which 3 and not 4 cards converge, but this is not very important). You can draw on the Lobachevsky plane a square grid, at each vertex of which 5 (or 6, or infinitely many) squares converge. And you can replace square cells with cubic ones and build a map in space.
')
I chose the last option. It was very interesting to see how the terrain map would look on a four-dimensional planet.
To begin with, it was necessary to decide which version of the game I would adapt: there are several different basic sets of cells and rules that also have extensions with additional elements and objects. The choice fell on the option "Discovery" (aka "New World", aka "New Earths"). There the land is divided into three areas (seas, mountains, plains), and for completed (and even unfinished) objects you can get points.
The first estimates showed that the three types of regions will be small: on average, the cube will have two faces of each color, and one can expect infinite growth of connected regions. Therefore, I immediately added a fourth type (desert) and set about implementing it.
Alas ... after only a few dozen tiles laid out, it became clear that it would not be possible to sort out the resulting map. The surface turned out to be too ragged, the translucent borders between areas of different colors were mixed, and it was impossible to understand how far this or that area stretches in any way:

Later I found a couple of ways giving a chance to make this option more or less understandable, so maybe I’ll come back to it. But so far it was necessary to look for something that allows you to make an interface that is clear and suitable for the game. And the following rules of simplicity were in the basic version of the game.
In the basic version there are four elements of topography: cities, roads, monasteries, and fields, which occupy the rest of the territory. Players in the process of the game can occupy roads (areas limited by ends or intersections), cities (areas limited by walls), monasteries (individual cells) and fields. For completed objects (except for fields) points are awarded (objects are released at the same time), and fields are evaluated only at the end of the game.
It is clear that in the three-dimensional case, the idea of a field, as an element of topography, does not work: roads do not divide the earth into parts, and in most cases the entire map turns out to be one large field interspersed with cities. To keep the interest, I added another similar pair to the cities and roads - the sea and the river. With a slightly different scoring: if a city is estimated by area, then the sea is based on the number of ports (cells where rivers flow into it and sections bordering cities), and in rivers, unlike roads, intersections are not the boundaries of the section. But these are all cosmetic edits. The first question is what the playing field will look like and what game cards will be.
For the game, it is necessary that the fragments of objects on the new cells continue unfinished objects that are already on the field. So, the edges of the cells should provide convenient opportunities for their joining. The easiest way to achieve this is to make the relief on the facets symmetrical — so that any two cells with faces of the same type can join along these faces in any of four possible ways. The selected game elements (plain, river, sea, road, city) provide such an opportunity: it is enough that the city and the sea can occupy the edges only as a whole, and the roads and rivers pass through the centers of the faces. If such a relief detail as canyons (two-dimensional surfaces that divide space into parts) were added, then this method would not work - we would have to take into account the mutual orientation of the cells relative to the axis passing through their centers. But in the current version of the game there are no canyons.
I divided the cell into 7 zones: 6 correspond to the faces and have the shape of truncated square pyramids, and the seventh - in the center, has the shape of a cube. External zones can be in one of 5 states (all but the monasteries), internal - in one of six. The geometry and topographic properties of a cell are completely determined by the states of its zones: two sections of the sea or a city belonging to adjacent faces are adjacent, if exactly two faces of the cell (and adjacent) are in the “road” state, then the road connects the centers of these faces (otherwise connects the face with the central zone). And there are a few limitations. For example, if a cell contains three or more roads, then the central zone should be a “city” (and play the role of an intersection).
I was afraid to list all possible cells, and I chose random generation: first, the state of all faces is determined by the cell (with certain probabilities: plain - with 1/2 probability, river and road - by 1/6, sea and city - by 1/12) , then the possible states of the central cell are determined. If a monastery is possible in the center, it is placed with a probability of 1/8, and if this does not happen, the state is chosen equiprobably from all possible. After that, the cell is offered for play. (Later, I considered that the number of different cells is about 750, so you can generate and include in the program a complete list of them, at the same time providing each with some probability of occurrence)
The starting cell looks like this:

It has fragments of the city, the river and the road. The cell is placed on the field, and the next cell is displayed in a separate window. For the move, you need to rotate the cage and the field so that the edge of the field to which we want to attach the cage was front, and the edge of the cage with which we want to attach it, looked towards it:

Use the left mouse button to rotate the cell and the field, and the right button to rotate the camera. To zoom in / out - Ctrl + left button.
After choosing the correct orientation, just click on the center of the edge of the field on which you want to put a cage, and if a move is possible, then it is done. After that, the player is offered to put one of his chips (if there are free - only 8 of them) on some part of the cell. Possible areas are represented by blue balls:

The player can click on one of the balls or click the "Skip" button (if he does not want to put a chip). The selected ball turns into an asterisk of color corresponding to this player, and the turn turns to the next one.

After a few moves, it becomes difficult to navigate the situation on the field:

To make life easier for players, there are several additional visualization modes. In order to analyze the outer edges of the cells on the field (and understand where you can walk), the outer edges of the field are made less transparent:

To better analyze the shape of individual objects, you can reduce their transparency and increase the transparency of the outer edges of the plain:

And finally, in order to more reliably determine the color of the chips on the field (for example, if the chip is in the sea or in the city), and just to see the position of all the chips, there is a mode in which all objects become white and almost transparent:

Before starting the game, you can select the number of players (from 2 to 5) and the duration of the game (the number of moves is from 20 to 10,000). After selecting them, click the New Game button.
Read more detailed rules (in English) can be
on this page . The executable code can be downloaded from here , and the source code from here . The program is written in C # using the Open Toolkit library. Requires Windows with .NET 2.0 to work
Source: https://habr.com/ru/post/135033/
All Articles