TPoDT keygenme analysis # 2
Good day to all.
It is me again, and again I carry reverse engineering topics to the masses. Since, for some reason, I cannot cover in my articles the analysis of commercial protectors or programs, so today our guinea pig will be the keygenme from the TPoDT group. Not to say that it is difficult, but it was not a pity to spend a few hours on it.
For those who do not know: keygenme is a type of program that is created by one cracker to analyze it with another. As a rule, the goal is to show some interesting mathematical algorithm or unusual code protection.
Download keygenme at this link . It is necessary to pay tribute to the authors - keygenme is not packed with anything, which saves us from unnecessary gestures. Yes, and apparently the authors have bothered to even make a nice interface.
We load into the debugger, and set breakpoints on the standard WinAPI functions used to get text from the input fields:
There are no unpleasant surprises, and we immediately stop at
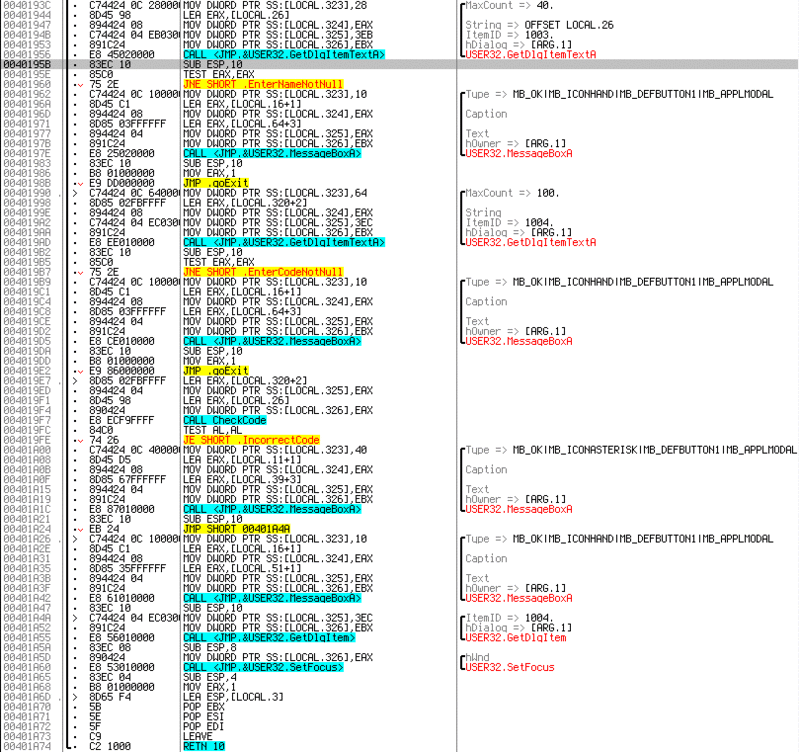
As you can see, the text is being read from the input fields, and if they are empty, MessageBox is shown with errors. Below you can see the entry to the
But we are interested in the algorithm itself, so the trace and go to
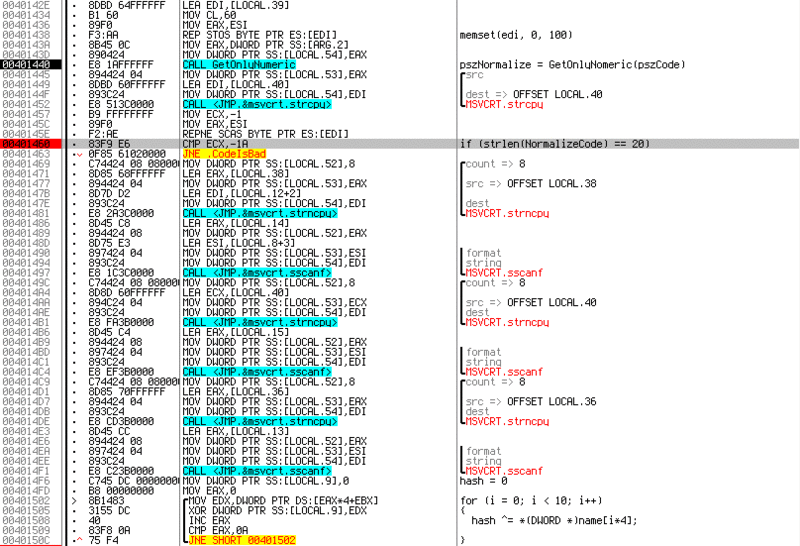
The code is pretty clean and easy to read. The first thing to do is call a
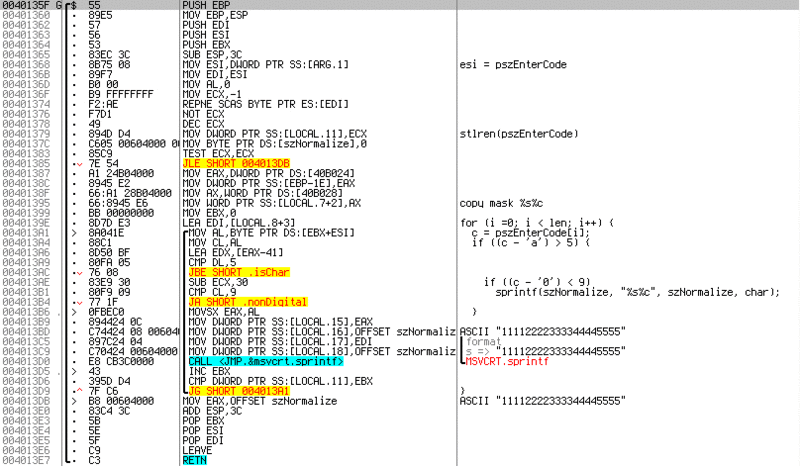
For C lovers, I specifically made comments on a C-like pseudocode. The code in the loop reads the entered string, and if the character does not lie in the range
Let's go back to the
Subsequent calls to the
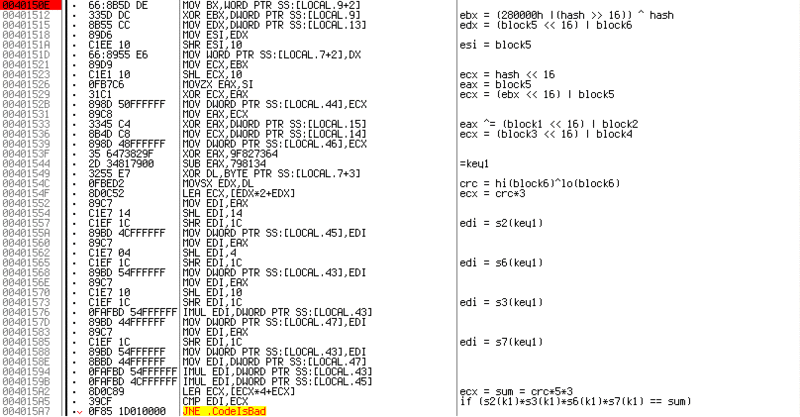
Personally, when examining programs, at first I look superficially at what it does, rub the code, and then analyze the necessary sections in the opposite direction from the checks.
In this case, the correct solution is when
Let's start with
In general, an
This is my variation, it is possible to put hyphens in a different way.
So, we have learned the right part of the condition, now we will move to the left part - to the calculation of EDI.
I will describe in brief what happens after
Now let's see what happens with the
which, for getting the original number from KEY1, can be reversed as follows:
At this stage, we will not try to substitute numbers, first we will look at the other checks.
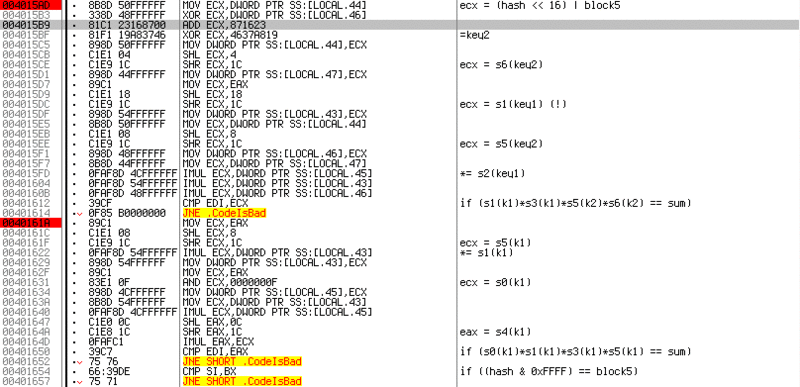
There are three of them in this screenshot. The first almost repeats the previous one. From the differences, you can select a change in the algorithm for calculating KEY2
Which just as easily turn in
And also, the semi-byte indexes have changed. Now take 5 and 6 from KEY2 and (!) 1, 2 from KEY1. That's why I said that you should not pick up the numbers, as they are still used further by the algorithm. In further checks, key numbers are no longer generated, but two received KEY1 and KEY2 are used.
The third check multiplies 0,1,4 and 5 half-bytes of KEY1.
At the very bottom of the screenshot, at
The first two of them are of the same type, and simply choose their half-bytes for multiplication from the key numbers. Therefore, I will not repeat. Greater attention deserves a check located at
The
Now a little math. At the very beginning we saw that the number with which the comparison is being made in checks is CRC * 15. And since we found above that CRC = 0x5B, it is not difficult to get SUM = CRC * 15 = 0x555 = 1365 (10).
In each check, when multiplying the half-bytes, 4 operands are always used, which means that we have to decompose the number 1365 into 4 factors. If divisibility by 3 and 5 is visible, then the remaining 7 and 13 are not so obvious. But in general, the task is not difficult. In the commercial version it was possible to take a larger number of factors and, accordingly, a much larger number, then the decomposition would take more time. We figured out the multipliers, now let's look at the half-byte sampling map at different iterations.
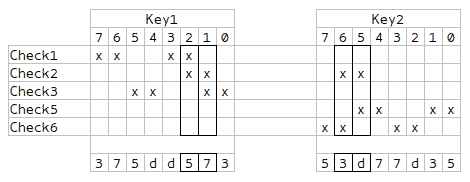
How could notice that 4 columns are selected - they intersect in a pair of checks, which means that these values need to be generated separately, and they should be all different. The rest of the semi-bytes can be selected randomly, with the condition that for each test there will be all 4 different multipliers.
At the same time, I noticed some symmetry, which allows us to generate not all, but only half of the values, and fill the rest with a mirror image.
I will analyze a small example for my nickname.
The hash from it will be equal to
KEY1 and KEY2 choose for example
Then to get block1-block4 you need to perform the following operations:
The fifth key block is the lower part of the hash. In my case - 622F. Well, in the last, sixth block, we have more options to choose - the general formula will be (c << 8) | (c ^ 0x5B). In the simplest case, 005B (00 ^ 5B = 5B).
The final key will be
If everything is found correctly, the following window should be displayed.
With my version of the key generator can be found here.
It is me again, and again I carry reverse engineering topics to the masses. Since, for some reason, I cannot cover in my articles the analysis of commercial protectors or programs, so today our guinea pig will be the keygenme from the TPoDT group. Not to say that it is difficult, but it was not a pity to spend a few hours on it.
For those who do not know: keygenme is a type of program that is created by one cracker to analyze it with another. As a rule, the goal is to show some interesting mathematical algorithm or unusual code protection.
Download keygenme at this link . It is necessary to pay tribute to the authors - keygenme is not packed with anything, which saves us from unnecessary gestures. Yes, and apparently the authors have bothered to even make a nice interface.

We load into the debugger, and set breakpoints on the standard WinAPI functions used to get text from the input fields:
GetDlgItem, GetDlgItemTextA, GetWindowTextA. We release the program for execution, we drive in any name, key, and click the 'Check' button.There are no unpleasant surprises, and we immediately stop at
GetDlgItemTextA . We remove bryaki, and exit the API - we are standing at the address 0x0040195B
As you can see, the text is being read from the input fields, and if they are empty, MessageBox is shown with errors. Below you can see the entry to the
CheckCode function, which returns 0 or 1 depending on the result of the check. And, respectively, below MessageBox pair on true and false option of check. It is worth noting that, despite the absurdity of such protection, it is found in almost half of the applications. And if the goal is simply to get a working application, not a key, then you can replace call with a sequencexor al, al inc al
But we are interested in the algorithm itself, so the trace and go to
CheckCode .
The code is pretty clean and easy to read. The first thing to do is call a
GetOnlyNumeric called by me GetOnlyNumeric , it is passed, as a parameter, a pointer to the entered code.
For C lovers, I specifically made comments on a C-like pseudocode. The code in the loop reads the entered string, and if the character does not lie in the range
'A'-'F' or '0'-'9' , then it skips the character. If the symbol satisfies the condition, then merges it with a new line. This is done so that you can enter the key in a "beautiful" form, with delimiters.Let's go back to the
CheckCode function code. At the address 0x00401457 you can see the counting of the length of the normalized string, and it should be equal to 24. (I have a typo here on the screenshot) . Why 24? REP SCASB searches the string for a character from AL , while decreasing the ECX . Initially, ECX is indicated by 0xFFFFFFFF as the maximum value. Usually after this, the NOT ECX and DEC ECX commands are executed in order to get the length of the string in a normal form. We will do the same-1Ah = FFFFFFE6h not FFFFFFE6hh = 19h 19h - 1 = 24dec
Subsequent calls to the
sscanf functions translate the normalized string into three binary DWORDs in a row. And at the very bottom of the screenshot there is a small loop that counts the hash from the entered name, by successive XOR ten DWORDs of the buffer. (Buffer 40 characters long) At this point, the initial preparations are finished and the checks begin.
Personally, when examining programs, at first I look superficially at what it does, rub the code, and then analyze the necessary sections in the opposite direction from the checks.
In this case, the correct solution is when
EDI=ECX Let's start with
ECX — right before the comparison, the LEA ECX, [ECX*4+ECX] In general, an
LEA is a command for calculating an address, but in this case it executes the expression: ECX = ECX*4 + ECX ECX*5 . Going up the code, ECX is now found at 0x0040154F LEA ECX, [EDX*2+EDX] ECX = EDX*3*5 EDX ? If you potreitsit code, we understand that it is equal to the XOR operation between the older and the younger part of the last key block. In the future, the resulting number will be called SUM, and poksorennye two bytes of the last block - CRC. Let me explain why the block - after translating the entered string into a binary form, all operations on them are performed either with a DWORD or with WORD values. Therefore, the type of key can be as follows:1111-2222-3333-4444-5555-6666
This is my variation, it is possible to put hyphens in a different way.
So, we have learned the right part of the condition, now we will move to the left part - to the calculation of EDI.
I will describe in brief what happens after
SUB EAX, 798134 ECX . The first thing that comes to mind is to calculate such values at which both crc and KEY1 would equal 0. It seems all is well, but it would be too simple, with this option all checks except the last one are passed. But more about that later.Now let's see what happens with the
EDX , before it becomes KEY1. From the comments it can be understood that at first it is considered from the younger part of the hash on behalf of block1 and block2, again using XOR . Then two operations are performed.XOR EAX, 9F827364 SUB EAX, 798134
which, for getting the original number from KEY1, can be reversed as follows:
ADD EAX, 798134 XOR EAX, 9F827364
At this stage, we will not try to substitute numbers, first we will look at the other checks.

There are three of them in this screenshot. The first almost repeats the previous one. From the differences, you can select a change in the algorithm for calculating KEY2
ADD ECX, 871623 XOR ECX, 4637A819
Which just as easily turn in
XOR ECX, 4637A819 SUB ECX, 871623
And also, the semi-byte indexes have changed. Now take 5 and 6 from KEY2 and (!) 1, 2 from KEY1. That's why I said that you should not pick up the numbers, as they are still used further by the algorithm. In further checks, key numbers are no longer generated, but two received KEY1 and KEY2 are used.
The third check multiplies 0,1,4 and 5 half-bytes of KEY1.
At the very bottom of the screenshot, at
0x00401654 , there is a very small check CMP SI, BX . It is not complicated, and again, by treys, you can see that the younger part of the hash is compared on behalf of the fifth block of the entered code. The remaining three checks are also small: 
The first two of them are of the same type, and simply choose their half-bytes for multiplication from the key numbers. Therefore, I will not repeat. Greater attention deserves a check located at
0x004016BF . Here it is, and it is the most insidious - it compares crc, or more simply the poksorennye bytes of the last block, on which all previous checks depend. And which actually does not allow us to make KEY1 and KEY2 zero.The
SHL EDX, 1 command shifts 1 bit to the left, which is equivalent to multiplying a number by 2. Thus, we find that the number of the poxor number is a constant for any code and should be 0xB6 / 2 = 0x5B.Now a little math. At the very beginning we saw that the number with which the comparison is being made in checks is CRC * 15. And since we found above that CRC = 0x5B, it is not difficult to get SUM = CRC * 15 = 0x555 = 1365 (10).
In each check, when multiplying the half-bytes, 4 operands are always used, which means that we have to decompose the number 1365 into 4 factors. If divisibility by 3 and 5 is visible, then the remaining 7 and 13 are not so obvious. But in general, the task is not difficult. In the commercial version it was possible to take a larger number of factors and, accordingly, a much larger number, then the decomposition would take more time. We figured out the multipliers, now let's look at the half-byte sampling map at different iterations.

How could notice that 4 columns are selected - they intersect in a pair of checks, which means that these values need to be generated separately, and they should be all different. The rest of the semi-bytes can be selected randomly, with the condition that for each test there will be all 4 different multipliers.
At the same time, I noticed some symmetry, which allows us to generate not all, but only half of the values, and fill the rest with a mirror image.
I will analyze a small example for my nickname.
The hash from it will be equal to
0x6930622F . The upper part is not involved in the algorithm.KEY1 and KEY2 choose for example
5d7337d5 d537735d .Then to get block1-block4 you need to perform the following operations:
(5d7337d5 + 798134) ^ 9F827364 = C26ECA6D block1 = C26E ^ 622F = A041 block2 = CA6D ^ 622F = A842 (d537735d ^ 4637A819) - 871623 = 9279C521 block3 = 9279 ^ 622F = F056 block4 = C521 ^ 622F = A70E
The fifth key block is the lower part of the hash. In my case - 622F. Well, in the last, sixth block, we have more options to choose - the general formula will be (c << 8) | (c ^ 0x5B). In the simplest case, 005B (00 ^ 5B = 5B).
The final key will be
A041-A842-F056-A70E-622F-005B
If everything is found correctly, the following window should be displayed.

With my version of the key generator can be found here.
')
Source: https://habr.com/ru/post/134817/
All Articles