Moving Average Algorithm (Simple Moving Average)
There was a task to implement a moving average algorithm in C ++, which is widely used in signal processing and statistics.
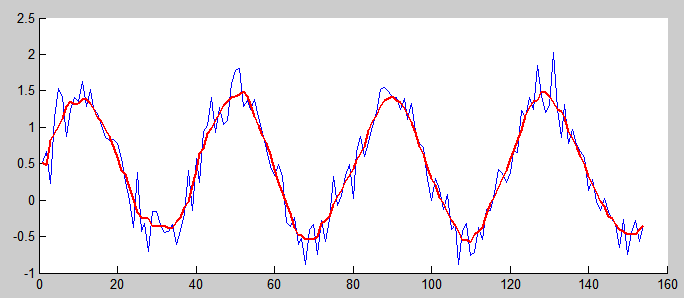
The smooth function in MATLAB was taken as the basis.
This function can be used to filter signals. As an input parameter, the data array and the averaging window are defined.
Who cares, I ask under the cat
So, there are several implementations of this algorithm. Consider the simplest of them:
suppose the averaging window is 5, then at each averaging step the current value is taken, 4 previous ones are added to it and the result is divided by 5. The obvious problem here is in the algorithm initialization, you first need to accumulate a certain amount of data not less than the averaging window.
In MATLAB, the filtering algorithm using the moving average is implemented in the smooth function
An example of using smooth (input, window) ,
where input is an input data array
window - averaging window.
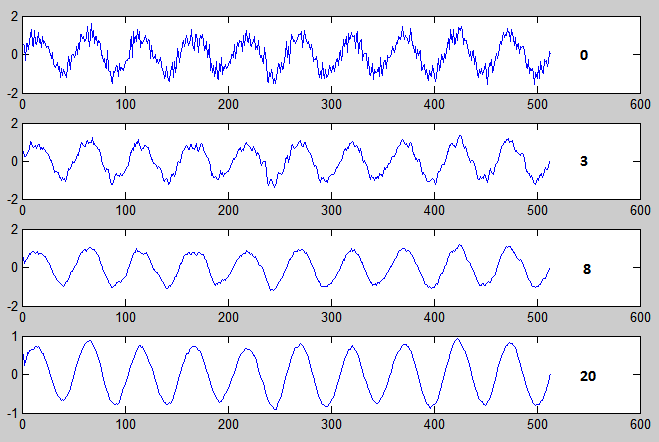
By changing the window parameter you can get a greater or lesser degree of data smoothing:
')
The source code that implements this example is presented below:
To compensate for the delay in signal processing, MATLAB uses a dynamically resizable window size, the following example illustrates the essence of the method:
I first wrote my own implementation of this algorithm in MATLAB, and then transferred it to C ++
MATLAB edition:
The result of the work of this program absolutely coincides with the matlabovsky smooth with odd window sizes and is somewhat different when it is even (the matlab even considers windows a little different)
The original m-file can be taken here.
C ++ Edition
Thank you for your attention, constructive criticism is welcome.
ps:
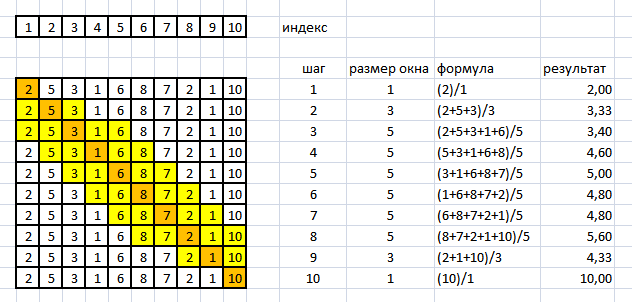
The algorithm can be optimized for speed by changing the counting amount:

It can be seen that to calculate the sum of the elements at the 4th step, you need to subtract the 1st element of the array (2, marked in red) from the sum at the third step and add the 6th element (8, yellow cell).
In the next step, the procedure is repeated.
This approach will be effective with a large averaging window.

The smooth function in MATLAB was taken as the basis.
This function can be used to filter signals. As an input parameter, the data array and the averaging window are defined.
Who cares, I ask under the cat
So, there are several implementations of this algorithm. Consider the simplest of them:
suppose the averaging window is 5, then at each averaging step the current value is taken, 4 previous ones are added to it and the result is divided by 5. The obvious problem here is in the algorithm initialization, you first need to accumulate a certain amount of data not less than the averaging window.
In MATLAB, the filtering algorithm using the moving average is implemented in the smooth function
An example of using smooth (input, window) ,
where input is an input data array
window - averaging window.
By changing the window parameter you can get a greater or lesser degree of data smoothing:

')
The source code that implements this example is presented below:
clear all; %% t=1;% Fd=512;% () A1=1;% F1=10;% () SNR=0.3;% / T=0:1/Fd:t;% Noise=A1*SNR*randn(1,length(T));% Signal=A1*sind((F1*360).*T);% SN=Signal+Noise; figure(1); subplot(4,1,1); plot(SN); subplot(4,1,2); plot(smooth(SN,3)); subplot(4,1,3); plot(smooth(SN,8)); subplot(4,1,4); plot(smooth(SN,20)); To compensate for the delay in signal processing, MATLAB uses a dynamically resizable window size, the following example illustrates the essence of the method:

I first wrote my own implementation of this algorithm in MATLAB, and then transferred it to C ++
MATLAB edition:
%my_smooth % , , 1 ; window = 5; if(mod(window,2)==0) window=window+1; end hw=(window-1)/2; % n=length(Signal); result=zeros(n,1); result(1)=SN(1); % SN for i=2:n % init_sum = 0; if(i<=hw) % , , % k1=1; % k2=2*i-1; % z=k2; % elseif (i+hw>n) % + n - % k1=i-n+i; % k2=n; % - z=k2-k1; % else % , k1=i-hw; k2=i+hw; z=window; end for j=k1:k2 % init_sum=init_sum+SN(j); % end result(i)=init_sum/(z); % end The result of the work of this program absolutely coincides with the matlabovsky smooth with odd window sizes and is somewhat different when it is even (the matlab even considers windows a little different)
The original m-file can be taken here.
C ++ Edition
void smooth(double *input, double *output, int n, int window) { int i,j,z,k1,k2,hw; double tmp; if(fmod(window,2)==0) window++; hw=(window-1)/2; output[0]=input[0]; for (i=1;i<n;i++){ tmp=0; if(i<hw){ k1=0; k2=2*i; z=k2+1; } else if((i+hw)>(n-1)){ k1=i-n+i+1; k2=n-1; z=k2-k1+1; } else{ k1=i-hw; k2=i+hw; z=window; } for (j=k1;j<=k2;j++){ tmp=tmp+input[j]; } output[i]=tmp/z; } Thank you for your attention, constructive criticism is welcome.
ps:
The algorithm can be optimized for speed by changing the counting amount:

It can be seen that to calculate the sum of the elements at the 4th step, you need to subtract the 1st element of the array (2, marked in red) from the sum at the third step and add the 6th element (8, yellow cell).
In the next step, the procedure is repeated.
This approach will be effective with a large averaging window.
Source: https://habr.com/ru/post/134375/
All Articles