Using Octave to calculate the center of rotation of a star field
I have already partially talked about working with FITS files in Octave. Now I will talk about the application of this mathematical package for processing specific data, namely: to calculate the center of rotation of the star field from a set of images taken at a certain interval.
To begin, let's touch the mathematical part. Geometrical transformations are mathematically convenient to present in vector-matrix form. So, for example, if we have a radius vector r that characterizes a given image point, then to get the radius vector of a point-mapping, r ', we must multiply the geometric transformation matrix, A , by r : r' = A · r . In the simplest case, A is a two-dimensional 2x2 matrix. However, for complex transformations it is necessary to expand it to the size of 3x3: for example, to describe the image displacement.
In the general case, the vectors r and r ' are column vectors of three elements: the actual coordinates of a point and one. The 3x3 transformation matrix itself has only six significant elements (the top two rows), and its third row contains two zeros and one unit.
In this case, the transformation of rotation relative to the origin of coordinates at an angle θ in the matrix form will be written as:
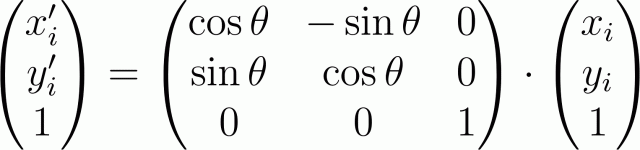
The significant members of the geometric transformation matrix carry the following meaning: the submatrix 2x2 of the upper left corner reflects transformations depending on the coordinates of the point (for example, rotation, scaling), and the upper two members of the rightmost column represent transformations that do not depend on the coordinates (offset).
')
Thus, for example, the rotation matrix around the origin of coordinates at an angle θ followed by this shift by the vector t will look like this:
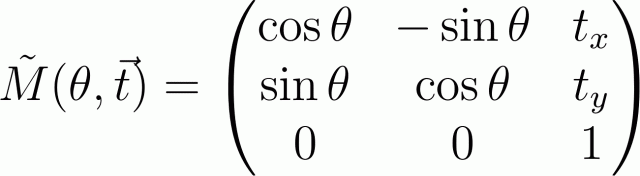
To obtain a matrix describing a more complex transformation, we will need to expand this motion into elementary (rotation, displacement, scaling) and multiply the corresponding matrices. Those who worked with openGL will have no difficulty in doing this. It is only necessary to remember that if the transformations are performed in the order A, B, C , then they will need to be multiplied "backwards": the resulting matrix is M = C · B · A (since the transformation A is first produced by multiplying A · r , the resulting vector is experiencing a conversion B and so on.
Rotation around an arbitrary point is decomposed into three elementary transformations: shift the image so that the origin is at the point of rotation (i.e. if the center of rotation is at the point (x, y), you need to shift by the vector (-x, -y) ) ; its rotation by the angle θ and the reverse shift by the vector (x, y) . As a result of this multiplication, the transformation matrix will be
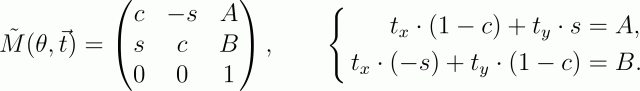
(for simplicity, I replaced sin θ with s, and cos θ with c).
If we designate the significant terms of the rotation matrix as the matrix R , then the last system of equations can be represented in the matrix form (IR) · t = AB , where AB is a column vector from the A and B terms of the final transformation matrix.
From here you can find the vector t , which characterizes the center of the image: t = (IR) \ AB , where the backslash denotes the operation of the "left" division (entry, adopted in Matlab and Octave): in algebra it is similar to the entry t = (IR) -1 AB ( I is the identity matrix).
If the rotation is accompanied by even small displacements, the vector AB will contain the additive term dr , which will introduce a significant error in the calculations (since the length of the vector AB is small when rotating at small angles). Mathematically, it is impossible to determine this shift, having only a couple of shots on hand. However, if we have a significant number of images, it is possible to calculate the median value of the center of rotation, and knowing it already it will be easy to determine small displacements dr .
So, let us have a set of images of the star field (this, by the way, can be an arbitrary image with reliably selected reference areas) and it is necessary to calculate the center of rotation of this field.
To begin, we need to select the stars (in general, reference points). In the specific case, this is solved by simple binarization at a given threshold (the threshold is selected as the maximum from the value set by the user and the sum of the median intensity value over the image plus a quarter of the standard deviation). Then, in the resulting binary image, zones with 8-coherence are detected and numbered in the order of detection. As a result, we get a set of masks with which we can calculate the centers of objects (in the simplest case, as an elementary center of gravity).
Next, we need to highlight the objects present in all images. I solved this problem head-on: for each image a set of vectors is constructed — the coordinates of the objects detected in the polar system relative to each object (that is, for a set of N points we get N · (N-1) vectors). For identification, all sets of vectors for the first and for the i-th image are sorted. Each set is given an estimate — the number of coincidences of the radius vectors of the points up to the user-set error dr, dφ. Then, a pair of sets with the highest score is selected and the objects of the i-th image are numbered, in accordance with the order of the objects of the first image. After each procedure of detecting objects of the first image on the i-th, the value of the counters corresponding to the detected objects of the first image increases. In parallel, the accumulation of the coordinates of the detected objects.
This “head-on” solution greatly slows down the calculations and consumes a lot of memory in case of a large number of objects detected and a large number of images, so the method can be simplified. For example, you can first compare the first and last image, having defined the set of points (which will reduce the memory consumption and the number of iterations); the search itself can also be performed only with respect to two or three objects of the first image (it is impossible to use the comparison of only one set, since a specific object can not be detected in the ith image).
After the end of the detection of objects, we get an array of counters. If the object is present on all images, the value of the corresponding counter should be equal to M-1 (M is the number of images). All data for which the counter is not equal to M-1 is deleted. Further, it is necessary only to compare the object coordinates for all images in pairs, calculating the center of rotation for each pair using the above formula (the transformation matrix is calculated by the least squares method). Having accumulated an array of coordinates of the center, we find the real center of rotation as the median of all coordinates.
In addition to my method, I found another method in this article (McKein et al.). The method is convenient in that it does not require finding the transformation matrix by the least squares method. It is based on the fact that the rotation around an arbitrary point can be represented more simply: as a rotation immediately relative to the origin of coordinates and the subsequent displacement. Instead of calculating the transformation matrix, the authors suggested determining the rotation angle of the entire system (which is easy to do using the coordinates of objects in the polar coordinate system relative to the center of gravity of the objects). The rotation angle is calculated by the rotation angle R. Multiplying this matrix by the radius vectors of the objects of the first image, we find the displacement vector, v (as the median of the difference between the radius vectors of the objects of the i-th image and the obtained radius vectors). The center of rotation is calculated using the same formula t = (IR) -1 v .
On a large amount of statistical material, both methods gave the same results. The choice of a particular method is determined by the implementation: in Octave, for example, my method is calculated faster, and the implementation of both methods is simple; When implementing an algorithm in C, it will be easier for McKein associates.
Here is the scatter of the found coordinates of the centers:
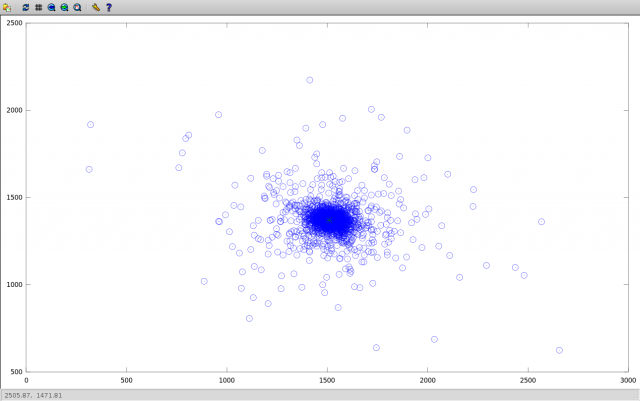
Emissions are explained by the fact that when comparing adjacent images (for which the angle of rotation is small), we get a very high error in the calculation of displacements, comparable to the error in calculating the coordinates of objects. The absolute deviation of the found coordinates relative to the median illustrates the above:

(outliers characteristic for close images then sharply decrease with increasing angle of rotation). Median averaging allows you to drop these outliers.
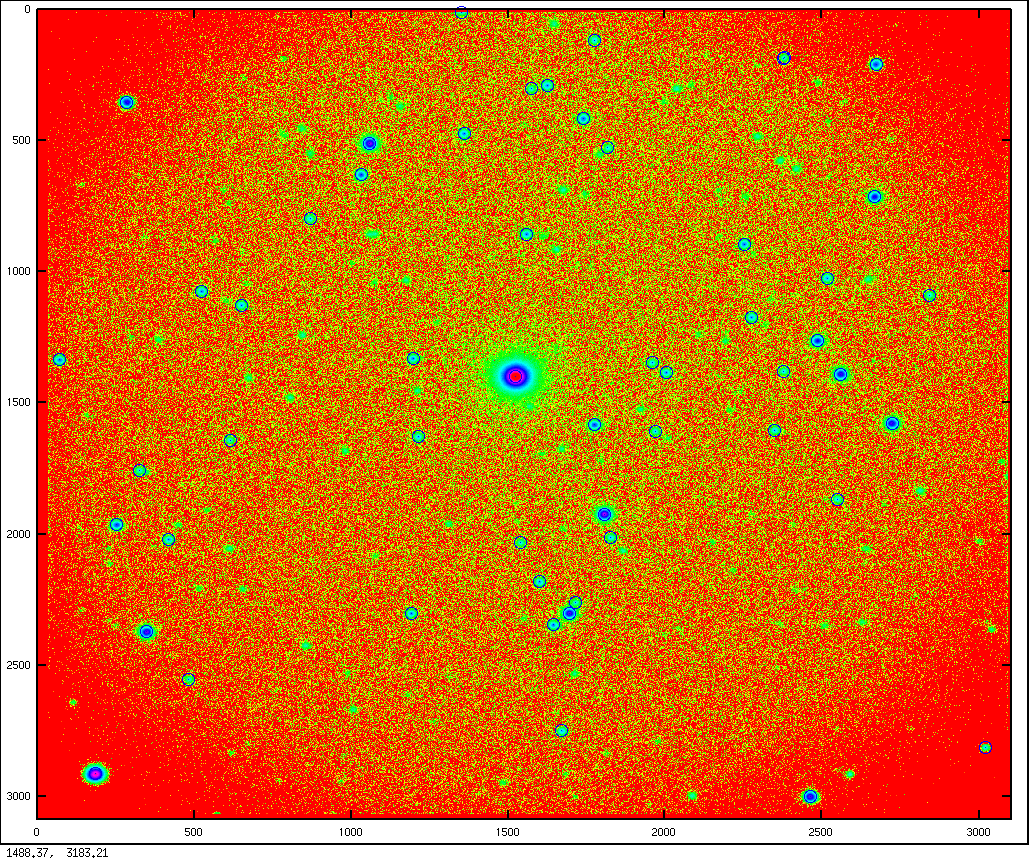
Yes, I almost forgot to give an example of the image of the star field. Here it is:
Reading FITS files:
Calculation of object centers:
Calculation of the coordinates of objects relative to the object number N:
Building a set of all relative coordinates of objects for a given image:
Obtaining compliance numbers of objects in two images:
Getting the arrays of coordinates of objects in all images in accordance with their numbering in the first image:
Getting the center of rotation:
The same, but by the McKein associates:
Geometric Transformations
To begin, let's touch the mathematical part. Geometrical transformations are mathematically convenient to present in vector-matrix form. So, for example, if we have a radius vector r that characterizes a given image point, then to get the radius vector of a point-mapping, r ', we must multiply the geometric transformation matrix, A , by r : r' = A · r . In the simplest case, A is a two-dimensional 2x2 matrix. However, for complex transformations it is necessary to expand it to the size of 3x3: for example, to describe the image displacement.
In the general case, the vectors r and r ' are column vectors of three elements: the actual coordinates of a point and one. The 3x3 transformation matrix itself has only six significant elements (the top two rows), and its third row contains two zeros and one unit.
In this case, the transformation of rotation relative to the origin of coordinates at an angle θ in the matrix form will be written as:
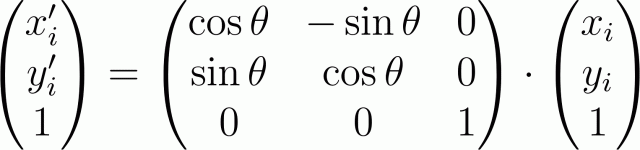
The significant members of the geometric transformation matrix carry the following meaning: the submatrix 2x2 of the upper left corner reflects transformations depending on the coordinates of the point (for example, rotation, scaling), and the upper two members of the rightmost column represent transformations that do not depend on the coordinates (offset).
')
Thus, for example, the rotation matrix around the origin of coordinates at an angle θ followed by this shift by the vector t will look like this:
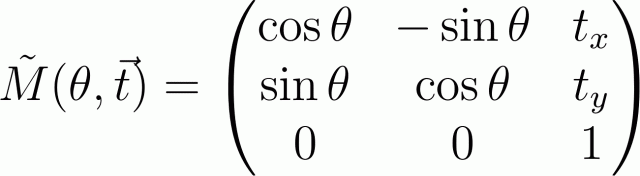
To obtain a matrix describing a more complex transformation, we will need to expand this motion into elementary (rotation, displacement, scaling) and multiply the corresponding matrices. Those who worked with openGL will have no difficulty in doing this. It is only necessary to remember that if the transformations are performed in the order A, B, C , then they will need to be multiplied "backwards": the resulting matrix is M = C · B · A (since the transformation A is first produced by multiplying A · r , the resulting vector is experiencing a conversion B and so on.
Rotation around an arbitrary point is decomposed into three elementary transformations: shift the image so that the origin is at the point of rotation (i.e. if the center of rotation is at the point (x, y), you need to shift by the vector (-x, -y) ) ; its rotation by the angle θ and the reverse shift by the vector (x, y) . As a result of this multiplication, the transformation matrix will be
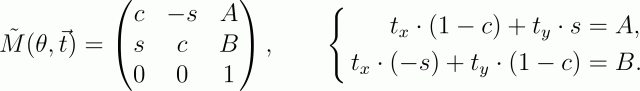
(for simplicity, I replaced sin θ with s, and cos θ with c).
If we designate the significant terms of the rotation matrix as the matrix R , then the last system of equations can be represented in the matrix form (IR) · t = AB , where AB is a column vector from the A and B terms of the final transformation matrix.
From here you can find the vector t , which characterizes the center of the image: t = (IR) \ AB , where the backslash denotes the operation of the "left" division (entry, adopted in Matlab and Octave): in algebra it is similar to the entry t = (IR) -1 AB ( I is the identity matrix).
If the rotation is accompanied by even small displacements, the vector AB will contain the additive term dr , which will introduce a significant error in the calculations (since the length of the vector AB is small when rotating at small angles). Mathematically, it is impossible to determine this shift, having only a couple of shots on hand. However, if we have a significant number of images, it is possible to calculate the median value of the center of rotation, and knowing it already it will be easy to determine small displacements dr .
Implementation in Octave
So, let us have a set of images of the star field (this, by the way, can be an arbitrary image with reliably selected reference areas) and it is necessary to calculate the center of rotation of this field.
To begin, we need to select the stars (in general, reference points). In the specific case, this is solved by simple binarization at a given threshold (the threshold is selected as the maximum from the value set by the user and the sum of the median intensity value over the image plus a quarter of the standard deviation). Then, in the resulting binary image, zones with 8-coherence are detected and numbered in the order of detection. As a result, we get a set of masks with which we can calculate the centers of objects (in the simplest case, as an elementary center of gravity).
Next, we need to highlight the objects present in all images. I solved this problem head-on: for each image a set of vectors is constructed — the coordinates of the objects detected in the polar system relative to each object (that is, for a set of N points we get N · (N-1) vectors). For identification, all sets of vectors for the first and for the i-th image are sorted. Each set is given an estimate — the number of coincidences of the radius vectors of the points up to the user-set error dr, dφ. Then, a pair of sets with the highest score is selected and the objects of the i-th image are numbered, in accordance with the order of the objects of the first image. After each procedure of detecting objects of the first image on the i-th, the value of the counters corresponding to the detected objects of the first image increases. In parallel, the accumulation of the coordinates of the detected objects.
This “head-on” solution greatly slows down the calculations and consumes a lot of memory in case of a large number of objects detected and a large number of images, so the method can be simplified. For example, you can first compare the first and last image, having defined the set of points (which will reduce the memory consumption and the number of iterations); the search itself can also be performed only with respect to two or three objects of the first image (it is impossible to use the comparison of only one set, since a specific object can not be detected in the ith image).
After the end of the detection of objects, we get an array of counters. If the object is present on all images, the value of the corresponding counter should be equal to M-1 (M is the number of images). All data for which the counter is not equal to M-1 is deleted. Further, it is necessary only to compare the object coordinates for all images in pairs, calculating the center of rotation for each pair using the above formula (the transformation matrix is calculated by the least squares method). Having accumulated an array of coordinates of the center, we find the real center of rotation as the median of all coordinates.
In addition to my method, I found another method in this article (McKein et al.). The method is convenient in that it does not require finding the transformation matrix by the least squares method. It is based on the fact that the rotation around an arbitrary point can be represented more simply: as a rotation immediately relative to the origin of coordinates and the subsequent displacement. Instead of calculating the transformation matrix, the authors suggested determining the rotation angle of the entire system (which is easy to do using the coordinates of objects in the polar coordinate system relative to the center of gravity of the objects). The rotation angle is calculated by the rotation angle R. Multiplying this matrix by the radius vectors of the objects of the first image, we find the displacement vector, v (as the median of the difference between the radius vectors of the objects of the i-th image and the obtained radius vectors). The center of rotation is calculated using the same formula t = (IR) -1 v .
On a large amount of statistical material, both methods gave the same results. The choice of a particular method is determined by the implementation: in Octave, for example, my method is calculated faster, and the implementation of both methods is simple; When implementing an algorithm in C, it will be easier for McKein associates.
Here is the scatter of the found coordinates of the centers:

Emissions are explained by the fact that when comparing adjacent images (for which the angle of rotation is small), we get a very high error in the calculation of displacements, comparable to the error in calculating the coordinates of objects. The absolute deviation of the found coordinates relative to the median illustrates the above:

(outliers characteristic for close images then sharply decrease with increasing angle of rotation). Median averaging allows you to drop these outliers.
Yes, I almost forgot to give an example of the image of the star field. Here it is:

Sources
Reading FITS files:
function [image header] = fits_read(filename) % % FITS- % y ! % ( flipdim, ) % % : % read_fits_image ( fits) % image = []; printf("Read file %s ... ", filename); fflush(1); % , : [ sem ] = stat(filename); if(e != 0 || !S_ISREG(s.mode)) printf("No such file!\n"); fflush(1); return; endif [ image header ] = read_fits_image(filename); if(!isempty(image)) image = flipdim(image',1); % , printf("OK!\n"); else printf("Bad image!\n"); endif fflush(1); endfunction Calculation of object centers:
function [ xc, yc ] = find_centers(Img, treshold) % [ xc, yc ] = find_centers(Img, treshold) % Img treshold % xc, yc - % tmp = zeros(size(Img)); mm = mean2(Img) + std2(Img)/4; % tres1 = max(mm, treshold); printf("\nTreshold: %g\n", tres1); fflush(stdout); tmp(find(Img > tres1)) = 1; tmp = medfilt2(logical(tmp)); [ Labels, Nlabels ] = bwlabel(tmp); if(Nlabels < 1) printf(stderr, "\nError! There's no spots!!!\n\n"); return endif [yy, xx] = ndgrid(1:size(Img,1),1:size(Img,2)); xc = []; yc = []; for i = [1 : Nlabels] idxs = find(Labels == i); Is = sum(Img(idxs)); xc = [ xc sum(Img(idxs) .* xx(idxs)) / Is ]; yc = [ yc sum(Img(idxs) .* yy(idxs)) / Is ]; end endfunction Calculation of the coordinates of objects relative to the object number N:
function coords = find_tree(xc, yc, N) % % coords = find_tree(xc, yc, N) % , xc yc, % N . % , - % , - . % if(size(xc, 1)) == 1 % , xc = xc'; endif if(size(yc, 1)) == 1 yc = yc'; endif if(size(xc) != size(yc) || N > size(xc, 1)) % coords = []; endif xn = xc(N); yn = yc(N); % N- Dx = xc - xn; Dy = yc - yn; % N- R = sqrt(Dx.^2+Dy.^2); % Phi = atan2(Dy,Dx)*180/pi; % coords = [R Phi]; endfunction Building a set of all relative coordinates of objects for a given image:
function [Tree xc yc] = get_tree(treshold, i) % % [Tree xc yc] = get_tree(treshold, i) % % : % treshold - % i - % : % Tree - , % * - % * - % * - % xc, yc - % % : % fits_read % find_tree % find_centers % Tree = []; xc = []; yc = []; name = sprintf("object_%04d.fit", i); II = fits_read(name); if(isempty(II)) return; endif printf("Find centers of %s ... ", name); fflush(1); [xc, yc] = find_centers(II, treshold); for j = 1:size(xc,2) Tree(:,:,j) = find_tree(xc, yc, j); endfor printf("done (%d vectors)!\n", size(Tree, 1)); endfunction Obtaining compliance numbers of objects in two images:
function coord_indexes = find_cluster_c(CC, CC1, dR, dPhi) % % coord_indexes = find_cluster_c(CC, CC1, dR, dPhi) % CC CC1 % : % CC, CC1 - % dR - R ( |r1-r0| < dR, , r1 == r0) % dPhi - % : % coord_indexes - [1 2; ...] % Ncc = size(CC, 3); Ncc1 = size(CC1, 3); % - Cluster = []; % : - , 1, 2, for jj = 1 : Ncc % Nnear = []; % , - PhiMed = []; % r0 = CC(:,1,jj); phi0 = CC(:,2,jj); for ii = 1 : Ncc1 % r1 = CC1(:,1,ii); phi1 = CC1(:,2,ii); points = {}; % ( 1; 2) dphi_s = []; % , for i = 1:size(r0); % d = abs(r1-r0(i)); % idx = find(d < dR); % r if(isempty(idx)) continue; endif; % - points = [ points; {i, idx} ]; % endfor for i = 1:size(points, 1) dphi = abs(phi1(points{i,2}) - phi0(points{i,1})); dphi_s = [dphi_s; dphi]; endfor if(isempty(dphi_s)) continue; endif; dphi = median(dphi_s); % 2 1 n = size(find(abs(dphi_s-dphi)<dPhi), 1); Nnear = [ Nnear, n ]; % PhiMed = [ PhiMed, dphi ]; endfor idx = find(Nnear == max(Nnear))(1); % , jj- Cluster = [ Cluster; Nnear(idx) jj idx PhiMed(idx) ]; endfor % n = max(Cluster(:,1)); % idx = find(Cluster(:,1) == n)(1); % first = Cluster(idx, 2); % 1 second = Cluster(idx, 3); % -//- 2 Phi = Cluster(idx, 4); % 2 1 r0 = CC(:,1,first); phi0 = CC(:,2,first); r1 = CC1(:,1,second); phi1 = CC1(:,2,second); coord_indexes = []; for i = 1:size(r0); % d = abs(r1-r0(i)); % idx = find(d < dR); % r if(isempty(idx)) continue; endif; % - dphi = abs(abs(phi1(idx) - phi0(i)) - Phi); if(size(idx, 1) != 1) % n = find(dphi == min(dphi))(1); % idx = idx(n); dphi = dphi(n); endif if(dphi > dPhi) continue; endif; % - coord_indexes = [ coord_indexes; i idx ]; endfor endfunction Getting the arrays of coordinates of objects in all images in accordance with their numbering in the first image:
function [XY] = get_centers(i0, i1, treshold, dR, dPhi) % % [XY] = get_centers(i0, i1, treshold, dR, dPhi) % X,Y % % : % i1, in - % treshold - % dR, dPhi - ( ) % : % X, Y - % % - % - % % : % get_tree -> fits_read, find_tree, find_centers % find_cluster_c % n = 1; % + X,Y i_start = i0; % CS = []; printf("\nimage 1\n", i); do [CC xc yc] = get_tree(treshold, i_start); im1 = i_start; i_start++; until(!isempty(CC) || i_start > i1) X = xc'; Y = yc'; % - Counters = zeros(size(X)); % for i = i_start:i1 [CC1 xc1 yc1] = get_tree(treshold, i); if(isempty(CC1)) continue; endif printf("\nimage %d, ", ++n); % indexes = find_cluster_c(CC, CC1, dR, dPhi); printf("%d points\n\n", size(indexes, 1)); % : X(indexes(:,1),n) = xc1(indexes(:,2)); Y(indexes(:,1),n) = yc1(indexes(:,2)); % Counters(indexes(:,1))++; endfor % , idx = find(Counters != n-1); X(idx,:) = []; Y(idx,:) = []; endfunction Getting the center of rotation:
function [Xc Yc] = matr_center(X, Y) % % [Xc Yc] = matr_center(X, Y) % , % : % X, Y - ( get_centers) % : % Xc, Yc - % Xc = []; Yc = []; imax = size(X,2); for i = 1:imax-1 for j = i+1:imax % X0 = X(:,i)'; X1 = X(:,j)'; Y0 = Y(:,i)'; Y1 = Y(:,j)'; % ( - ) vec0X = X0 - mean(X0); vec0Y = Y0 - mean(Y0); vec1X = X1 - mean(X1); vec1Y = Y1 - mean(Y1); % , %phi0 = atan2(vec0Y, vec0X); phi1 = atan2(vec1Y, vec1X); %% 2, -pi+a -> pi-b %phi0(find(phi0<0)) += 2*pi; phi1(find(phi1<0)) += 2*pi; %dphi = median(phi1 - phi0); % %R = [cos(dphi) -sin(dphi); sin(dphi) cos(dphi)]; % %RR1 = R * [vec0X;vec0Y]; % , 0 %dR = sqrt((vec1X-RR1(1,:)).^2+(vec1Y-RR1(2,:)).^2); % %idx = find(dR < median(dR)+std(dR)); % %if(size(idx,2) < 3) % %printf("Image %d: too much bad data\n", i); %continue; %endif %X0 = X0(idx); X1 = X1(idx);Y0 = Y0(idx); Y1 = Y1(idx); % A = [X1;Y1;ones(size(X1))]/[X0;Y0;ones(size(X1))]; % CRDS = (eye(2)-A(1:2,1:2)) \ A(1:2,3); Xc = [Xc CRDS(1)]; Yc = [Yc CRDS(2)]; % endfor endfor Xmed = median(Xc) Ymed = median(Yc) endfunction The same, but by the McKein associates:
function [Xc Yc] = matr_center_notmine(X, Y) % % [Xc Yc] = matr_center(X, Y) % , % : % X, Y - ( get_centers) % : % Xc, Yc - % Xc = []; Yc = []; imax = size(X,2); for i = 1:imax-1 for j = i+1:imax % X0 = X(:,i)'; X1 = X(:,j)'; Y0 = Y(:,i)'; Y1 = Y(:,j)'; % ( - ) vec0X = X0 - mean(X0); vec0Y = Y0 - mean(Y0); vec1X = X1 - mean(X1); vec1Y = Y1 - mean(Y1); phi0 = atan2(vec0Y, vec0X); phi1 = atan2(vec1Y, vec1X); % 2, -pi+a -> pi-b phi0(find(phi0<0)) += 2*pi; phi1(find(phi1<0)) += 2*pi; dphi = median(phi1 - phi0); % R = [cos(dphi) -sin(dphi); sin(dphi) cos(dphi)]; % % v v = median(R * [X0; Y0] - [X1; Y1], 2); % CRDS = (eye(2)-R) \ v; %printf("Center: (%g, %g)\n", CRDS(1), CRDS(2)); Xc = [Xc -CRDS(1)]; Yc = [Yc -CRDS(2)]; % endfor endfor Xmed = median(Xc) Ymed = median(Yc) endfunction Source: https://habr.com/ru/post/134352/
All Articles