Square root extraction using normal Markov algorithms
I wanted once to calculate the square root using normal Markov algorithms (NAM).
Briefly about us:
So, everything seems to be simple? However, how to write programs on US?
For myself, I made a plan like this:
So back to the square root calculation. We will use the “childish” method (aka arithmetic), which is based on the simple fact that the square of a number is the sum of odd numbers from 1 to 2n-1:
How could we implement root extraction based on this property? We will successively subtract from the number first 1, then 3, then 5, etc., until the number becomes less than zero, considering in parallel how many subtractions we made. Total already two counters + one variable to store the result
A little feature of US - there are no numbers here. And there are no variables. Therefore, we should simulate them. Since I was too lazy to write long arithmetic (and I doubt that this is possible for a person), I did arithmetic operations on a simple principle - with the help of increment and decrement.
')
I decided to make sure that my string is stored in the format {Result}. {Number} {Another Odd Numbers} {End-of-Line Indicator}
I decided to store the odd number in the unary calculus system and designate the unit as "#" - it will be so much easier to work.
Now, how will we subtract from the next odd number without losing data? I decided that between the odd number and the end of line indicator I need to add the marker “a”, which, moving through the number will duplicate it, but in a different form (denoted by “-”). After we move all the minuses to the number and take them away. After we have taken away all the numbers, we need to increase the result by one.
In my implementation there was a small feature - the result always goes rounded up. I decided to make this algorithm work with absolute accuracy of 0.5, and not 1 (as in the description). When the line remains cons more than half of their initial value, we must take and reduce the result.
The result was a "ping-pong", which extracts the square root of a given number.
The dependence of the number of substitutions on the number looks very interesting: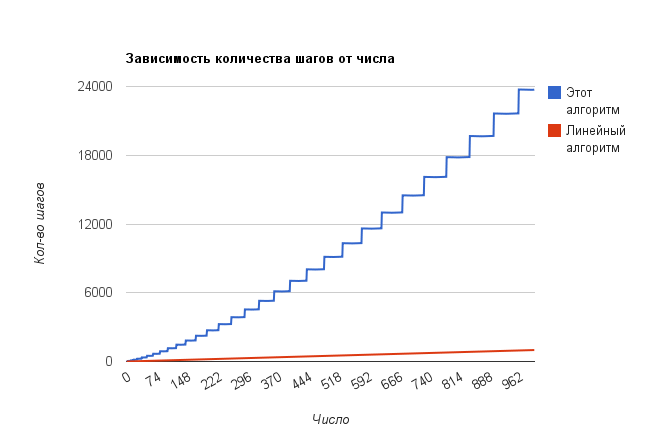
View code: paste.org.ru/?3uweqh
View execution example: paste.org.ru/?34caeb
Download the program: sites.google.com/site/nsinreal/markovsqrt.zip
Briefly about us:
- There is a list of substitutions from one substring to another, called rules
- We search from the beginning of the list for the first rule that we can apply and apply it to the first entry.
- If such a rule was found, then we return to the previous item and review the list of rules first.
- If the rule was final, then we complete the work.
- If there are no more rules that we can apply, then complete the work.
So, everything seems to be simple? However, how to write programs on US?
For myself, I made a plan like this:
- Trying to write a regular algorithm using only strings.
- Make sure that the latest replacements do not overlap with the first
- We turn over the algorithm and write from the end to the beginning
So back to the square root calculation. We will use the “childish” method (aka arithmetic), which is based on the simple fact that the square of a number is the sum of odd numbers from 1 to 2n-1:
- 1 = 1 2 = 1
- 1 + 3 = 2 2 = 4
- 1 + 3 + 5 = 3 2 = 9
How could we implement root extraction based on this property? We will successively subtract from the number first 1, then 3, then 5, etc., until the number becomes less than zero, considering in parallel how many subtractions we made. Total already two counters + one variable to store the result
A little feature of US - there are no numbers here. And there are no variables. Therefore, we should simulate them. Since I was too lazy to write long arithmetic (and I doubt that this is possible for a person), I did arithmetic operations on a simple principle - with the help of increment and decrement.
')
I decided to make sure that my string is stored in the format {Result}. {Number} {Another Odd Numbers} {End-of-Line Indicator}
I decided to store the odd number in the unary calculus system and designate the unit as "#" - it will be so much easier to work.
Now, how will we subtract from the next odd number without losing data? I decided that between the odd number and the end of line indicator I need to add the marker “a”, which, moving through the number will duplicate it, but in a different form (denoted by “-”). After we move all the minuses to the number and take them away. After we have taken away all the numbers, we need to increase the result by one.
In my implementation there was a small feature - the result always goes rounded up. I decided to make this algorithm work with absolute accuracy of 0.5, and not 1 (as in the description). When the line remains cons more than half of their initial value, we must take and reduce the result.
The result was a "ping-pong", which extracts the square root of a given number.
The dependence of the number of substitutions on the number looks very interesting:

View code: paste.org.ru/?3uweqh
View execution example: paste.org.ru/?34caeb
Download the program: sites.google.com/site/nsinreal/markovsqrt.zip
Source: https://habr.com/ru/post/133893/
All Articles