Reduced matrix multiplication exponent
News from the world of science: matrix size  now know how to multiply by
now know how to multiply by 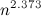 . In other words, it is proven that
. In other words, it is proven that 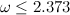 where
where 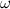 - exponential multiplication of matrices . Virginia Wasilewska-Williams proved this quite recently, thereby improving the
- exponential multiplication of matrices . Virginia Wasilewska-Williams proved this quite recently, thereby improving the 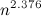 obtained by Coppersmith and Vinograd in 1987. I will write about the importance of this algorithm quite a bit. Those interested in learning more can read Scott Aaronson , Richard Lipton, and Bill Gasarsh .
obtained by Coppersmith and Vinograd in 1987. I will write about the importance of this algorithm quite a bit. Those interested in learning more can read Scott Aaronson , Richard Lipton, and Bill Gasarsh .
So, many theoretical upper bounds on the running time of the algorithms use the matrix multiplication exponent. In particular, many algorithms on graphs exploit this idea: if A is a graph adjacency matrix, then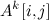 - the number of (not necessarily simple!) Paths of length k between vertices i and j. This simple idea allows for time
- the number of (not necessarily simple!) Paths of length k between vertices i and j. This simple idea allows for time 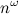 check if there is a triangle in the graph (3-cliques): you need to build an adjacency matrix into a cube (this will require two matrix multiplications) and look at the diagonal. Note that we are talking here about theoretical estimates, because the advanced matrix multiplication algorithms even overtake the asymptotically simple cubic algorithm, but in practice they only accelerate on the enormous dimensions of the matrices.
check if there is a triangle in the graph (3-cliques): you need to build an adjacency matrix into a cube (this will require two matrix multiplications) and look at the diagonal. Note that we are talking here about theoretical estimates, because the advanced matrix multiplication algorithms even overtake the asymptotically simple cubic algorithm, but in practice they only accelerate on the enormous dimensions of the matrices.
Some more examples:
 now know how to multiply by
now know how to multiply by 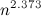 . In other words, it is proven that
. In other words, it is proven that 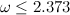 where
where 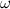 - exponential multiplication of matrices . Virginia Wasilewska-Williams proved this quite recently, thereby improving the
- exponential multiplication of matrices . Virginia Wasilewska-Williams proved this quite recently, thereby improving the 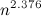 obtained by Coppersmith and Vinograd in 1987. I will write about the importance of this algorithm quite a bit. Those interested in learning more can read Scott Aaronson , Richard Lipton, and Bill Gasarsh .
obtained by Coppersmith and Vinograd in 1987. I will write about the importance of this algorithm quite a bit. Those interested in learning more can read Scott Aaronson , Richard Lipton, and Bill Gasarsh .So, many theoretical upper bounds on the running time of the algorithms use the matrix multiplication exponent. In particular, many algorithms on graphs exploit this idea: if A is a graph adjacency matrix, then
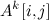 - the number of (not necessarily simple!) Paths of length k between vertices i and j. This simple idea allows for time
- the number of (not necessarily simple!) Paths of length k between vertices i and j. This simple idea allows for time 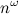 check if there is a triangle in the graph (3-cliques): you need to build an adjacency matrix into a cube (this will require two matrix multiplications) and look at the diagonal. Note that we are talking here about theoretical estimates, because the advanced matrix multiplication algorithms even overtake the asymptotically simple cubic algorithm, but in practice they only accelerate on the enormous dimensions of the matrices.
check if there is a triangle in the graph (3-cliques): you need to build an adjacency matrix into a cube (this will require two matrix multiplications) and look at the diagonal. Note that we are talking here about theoretical estimates, because the advanced matrix multiplication algorithms even overtake the asymptotically simple cubic algorithm, but in practice they only accelerate on the enormous dimensions of the matrices.Some more examples:
- The distances between all pairs of vertices (all-pairs shortest path).
The shortest paths between all pairs of vertices in an unweighted graph can be found in time. . To do this, we raise the adjacency matrix to the power n (from here, o (1) gets out to the power), simultaneously calculating the shortest paths. Learn more, as well as many other similar elegant algorithms from
. To do this, we raise the adjacency matrix to the power n (from here, o (1) gets out to the power), simultaneously calculating the shortest paths. Learn more, as well as many other similar elegant algorithms from
excellent presentation of Uri Zwick. - The task of maximum 2-satisfiability (MAX-2-SAT).
The only known algorithm for this problem, which is faster than brute force (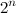 ), is also based on the multiplication of matrices. His work time is equal to
), is also based on the multiplication of matrices. His work time is equal to  and it uses exponential memory. In a nutshell, the idea is this: according to the input formula we build a huge graph (on
and it uses exponential memory. In a nutshell, the idea is this: according to the input formula we build a huge graph (on  vertices) and using the fast multiplication of matrices, we check if there is a triangle in it. It is noteworthy that he invented his husband Virginia - Ryan Williams.
vertices) and using the fast multiplication of matrices, we check if there is a triangle in it. It is noteworthy that he invented his husband Virginia - Ryan Williams. - Hamiltonian way (Hamiltonian cycle).
There is also such a funny example, in which it is not so important how much we can multiply matrices, but still. Algorithm for searching Hamiltonian paths in time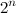 and polynomial memory (note that the famous Held-Karp algorithm for this problem is based on dynamic programming and requires exponential memory): it calculates the number of paths of length n-1 on all subsets of the graph vertices using the trick indicated above; after this, the inclusion-exclusion formula allows summing the found numbers so that only the number of simple paths of length n-1 remains (and this is the Hamiltonian path).
and polynomial memory (note that the famous Held-Karp algorithm for this problem is based on dynamic programming and requires exponential memory): it calculates the number of paths of length n-1 on all subsets of the graph vertices using the trick indicated above; after this, the inclusion-exclusion formula allows summing the found numbers so that only the number of simple paths of length n-1 remains (and this is the Hamiltonian path).
')
Source: https://habr.com/ru/post/133875/
All Articles