Algorithms LZW, LZ77 and LZ78

I want to continue my previous topic about compression algorithms . This time I will talk about the LZW algorithm and a little about its relatives the LZ77 and LZ78 algorithms.

LZW algorithm

The Lempel-Ziv-Welch Algorithm (Lempel-Ziv-Welch, LZW) is a universal lossless data compression algorithm.

An immediate predecessor of LZW was the LZ78 algorithm, published by Abraham Lempel and Jacob Ziv in 1978. This algorithm was perceived as a mathematical abstraction until 1984, when Terry A. Welch published his work with the modified algorithm, later called LZW (Lempel-Ziv-Welch).

Description

The compression process is as follows. The characters of the input stream are sequentially read and a check is made whether such a string exists in the created row table. If such a string exists, the next character is read, and if the string does not exist, the code for the previous found string is entered into the stream, the string is entered into the table, and the search begins again.
For example, if byte data (text) is compressed, then the rows in the table will be 256 (from "0" to "255"). If a 10-bit code is used, then the codes for the rows will contain values ​​in the range from 256 to 1023. New lines form the table sequentially, i.e., the row index can be considered its code.
The input decoding algorithm requires only encoded text, since it can recreate the corresponding conversion table directly from the encoded text. The algorithm generates a uniquely decoded code due to the fact that every time a new code is generated, a new row is added to the table of rows. LZW constantly checks if the string is already known, and, if so, outputs the existing code without generating a new one. Thus, each line will be stored in a single copy and have its own unique number. Consequently, when decrypting when a new code is received, a new line is generated, and when it is already known, a line is extracted from the dictionary.
')

Pseudocode algorithm

1. Initialization of the dictionary with all possible single-character phrases. Initialization of the input phrase ω by the first character of the message.
2. Read the next character K from the encoded message.
3. If END MESSAGE, then issue a code for ω, otherwise:
4. If the phrase ω (K) is already in the dictionary, assign the value ω (K) to the input phrase and go to Step 2, otherwise give the code ω, add ω (K) to the dictionary, assign the value K to the input phrase and go to Step 2.
5. the end

Example

Just by pseudo-code, it is not very easy to understand the operation of the algorithm, so let's consider Consider an example of image compression and decoding.
First, create an initial dictionary of single characters. In the standard ASCII code there are 256 different characters, therefore, in order for all of them to be correctly encoded (if we do not know which characters will be present in the source file and which ones will not), the initial code size will be equal to 8 bits. If we know in advance that there will be a smaller number of different characters in the source file, it is quite reasonable to reduce the number of bits. To initialize the table, we set the correspondence of code 0 to the corresponding symbol with bit code 00000000, then 1 corresponds to the symbol with code 00000001, etc., up to code 255. In fact, we indicated that each code from 0 to 255 is root.
There will be no other codes with this property in the table anymore.
As the dictionary grows, the size of the groups must grow in order to accommodate new elements. 8-bit groups give 256 possible combinations of bits, so when the 256th word appears in the dictionary, the algorithm should go to 9-bit groups. When the 512th word appears, a transition to 10-bit groups will occur, which makes it possible to memorize already 1024 words, etc.
In our example, the algorithm knows in advance that only 5 different characters will be used, therefore, the minimum number of bits will be used to store them, allowing us to remember them, that is, 3 (8 different combinations).

Coding

May we compress the sequence "abacabadabacabae".

• Step 1: Then, according to the algorithm outlined above, we will add the “a” line to the initially empty line and check if there is a line “a” in the table. Since during initialization we entered into the table all the rows of one character, the string “a” is in the table.
• Step 2: Next, we read the next “b” from the input stream and check if there is a string “ab” in the table. There is no such line in the table yet.
• Add to table <5> “ab”. To stream: <0>;
• Step 3: “ba” is not. In the table: <6> “ba”. To stream: <1>;
• Step 4: “ac” is not. In the table: <7> “ac”. To stream: <0>;
• Step 5: “ca” is not. To the table: <8> “ca”. To stream: <2>;
• Step 6: “ab” is in the table; “Aba” is not. To the table: <9> “aba”. To stream: <5>;
• Step 7: “ad” is not. To the table: <10> “ad”. To stream: <0>;
• Step 8: “da” - no. To the table: <11> “da”. To stream: <3>;
• Step 9: “aba” is in the table; “Abac” is not. To the table: <12> “abac”. To stream: <9>;
• Step 10: “ca” is in the table; “Cab” is not. To the table: <13> “cab”. To stream: <8>;
• Step 11: “ba” is in the table; “Bae” - no. To the table: <14> “bae”. To stream: <6>;
• Step 12: And finally, the last line is “e”, followed by the end of the message, so we just put <4> into the stream.

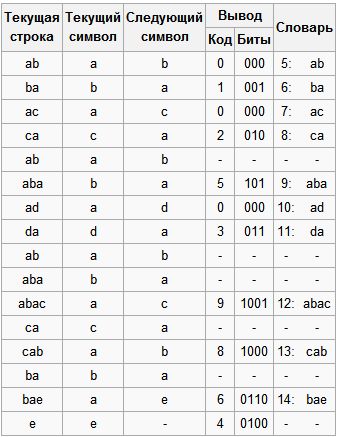
So, we get the coded message “0 1 0 2 5 0 3 9 8 6 4”, which is 11 bits shorter.

Decoding

The peculiarity of LZW is that for decompression we don’t need to save the string table to a file for unpacking. The algorithm is constructed in such a way that we are able to restore the table of rows using only the stream of codes.
Now imagine that we got the encoded message above, and we need to decode it. First of all, we need to know the initial vocabulary, and we can reconstruct the subsequent entries of the vocabulary on the go, since they are simply a concatenation of previous entries.

Addition

To increase the degree of image compression by this method, one “trick” of the implementation of this algorithm is often used. Some files subjected to compression using LZW have often found chains of identical characters, for example aaaaaa ... or 30, 30, 30 ..., etc. Their direct compression will generate the output code 0, 0, 5, etc. The question is, is it possible in this particular case to increase the degree of compression?
It turns out that this is possible if you specify some actions:
We know that for each code it is necessary to add to the table a row consisting of the line already present there and the character with which the next line begins in the stream.

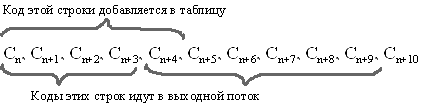
• So, the encoder enters the first “a” into the string, searches and finds the “a” in the dictionary. Adds the following “a” to the line, finds that “aa” is not in the dictionary. Then he adds the entry <5>: “aa” to the dictionary and outputs the <0> (“a”) label to the output stream.
• Next, the line is initialized to the second “a”, that is, it takes the form “a?” And the third “a” is entered, the line is again equal to “aa”, which is now in the dictionary.
• If the fourth "a" appears, then the string "aa?" Is equal to "aaa", which is not in the dictionary. The dictionary is replenished with this line, and the output is <5> (“aa”).
• After that, the string is initialized with the third "a", etc. etc. The further process is quite clear.
• As a result, the output is a sequence of 0, 5, 6 ..., which is shorter than the direct encoding using the standard LZW method.

It can be shown that such a sequence will be correctly restored. The decoder first reads the first code - this is <0>, which corresponds to the symbol “a”. Then it reads the code <5>, but this code is not in its table. But we already know that such a situation is possible only in the case when the character being added is equal to the first character of the sequence just read, that is, “a”. Therefore, he will add the string “aa” with the code <5> to his table, and put “aa” into the output stream. And so the whole chain of codes can be decoded.
Moreover, the coding rule described above can be applied in the general case not only to consecutive identical characters, but also to sequences in which the next added character is equal to the first character of the chain.

Advantages and disadvantages

+ Does not require the calculation of the probabilities of occurrence of characters or codes.
+ For decompression, you do not need to save the string table to a file for unpacking. The algorithm is constructed in such a way that we are able to restore the table of rows using only the stream of codes.
+ This type of compression does not distort the source image file, and is suitable for compressing raster data of any type.
- The algorithm does not analyze the input data is therefore not optimal.

Application

The publication of the LZW algorithm made a big impression on all information compression specialists. This was followed by a large number of programs and applications with different variants of this method.
This method allows you to achieve one of the best compression ratios among other existing methods of compressing image data, with no losses or distortions in the source files. Currently used in TIFF, PDF, GIF, PostScript and other files, and also in part in many popular data compression programs (ZIP, ARJ, LHA).

Algorithms LZ77 and LZ78

LZ77 and LZ78 - lossless compression algorithms, published in the articles of Abraham Lempel and Jacob Ziv in 1977 and 1978. These algorithms are best known in the LZ * family, which also includes LZW, LZSS, LZMA and other algorithms. Both algorithms refer to algorithms with a dictionary approach. LZ77 uses the so-called “sliding window”, which is equivalent to the implicit use of the vocabulary approach first proposed in LZ78.

LZ77 working principle

The basic idea of ​​the algorithm is to replace a repeated entry of a string with a reference to one of the previous entry positions. To do this, use the sliding window method. A sliding window can be presented in the form of a dynamic data structure, which is organized in such a way as to remember the information “said” earlier and provide access to it. Thus, the process of compressing coding according to LZ77 resembles the writing of a program whose commands allow access to elements of a sliding window, and instead of values ​​of a compressible sequence, insert references to these values ​​in a sliding window. In the standard LZ77 algorithm, line matches are encoded by a pair:

• match length
• offset (offset) or distance (distance)

The coded pair is interpreted precisely as a command for copying characters from a sliding window from a specific position, or literally as: “Return to the dictionary for the value of the character offset and copy the value of the length of characters starting from the current position.” A feature of this compression algorithm is that the use of a length-offset encoded pair is not only acceptable, but also effective in cases where the length value exceeds the offset value. The example with the copy command is not quite obvious: "Go back 1 character back in the buffer and copy 7 characters starting from the current position." How can I copy 7 characters from the buffer when there is currently only 1 character in the buffer? However, the following interpretation of the coding pair may clarify the situation: every 7 subsequent symbols are the same (equivalent) with 1 symbol in front of them. This means that each character can be unambiguously determined by moving back in the buffer, even if this character is still missing in the buffer at the time of decoding the current length-offset pair.

Algorithm Description

The LZ77 uses a sliding window. Suppose the window is fixed at the current iteration. On the right side of the window, we expand the substring while it is in the line <sliding window + stackable line> and starts in a sliding window. Let's call the stackable string buffer. After the extension, the algorithm produces a code consisting of three elements:

• window offset;
• buffer length;
• last character buffer.

At the end of the iteration, the algorithm shifts the window by a length equal to the length of the buffer + 1.

Kababababz example

Algorithm Description LZ78

Unlike LZ77, which works with already received data, LZ78 focuses on data that will only be received (LZ78 does not use a sliding window, it stores a dictionary of already viewed phrases). The algorithm reads the characters of the message until the accumulated substring is included entirely in one of the dictionary phrases. As soon as this line no longer corresponds to at least one dictionary phrase, the algorithm generates a code consisting of the index of the line in the dictionary, which until the last character entered contained the input string, and the character that violated the match. Then the entered substring is added to the dictionary. If the dictionary is already full, then the phrase used in the comparisons is deleted from it beforehand. If at the end of the algorithm we do not find the character that violated the coincidence, then we give the code in the form (the index of the line in the dictionary without the last character, the last character).

Kababababz example