Theory of Six Handshakes: Another Confirmation
Once, in the icy winter season, I was confronted with the mention that someone on Facebook was trying to confirm the theory of six handshakes. For those who do not know, this theory is that all the inhabitants of the earth, on average, know each other through a chain of five friends (that is, six handshakes). You can read more about the history of this theory in Wikipedia , and there you can find out that Microsoft tried to confirm this theory a few years ago on the basis of data on the contact lists of the MSN messenger - as a result, they got 6.6 handshakes, which fits into the theory.
I really wanted to confirm this theory myself, using the data at hand - VKontakte. To translate my strange idea into reality, it was necessary to solve a whole range of problems:
With the dominance of social networks in modern life, the question of where to get data on social relations is not so difficult. Of course, it would be great to take data about friends from Facebook, because it covers the whole world, and there are a lot of people there. But through a public API, I can’t pull out a friends list for any person, and parsing a page is not the most effective option, because Facebook spits out a list of friends in the form of dhtml, approximately 1kb of data per friend, for a total of 400M people * 130 friends on average * 1kb = 52 TB of traffic. Such a small amount of traffic did not fit into the research budget that was nulled to zero, and the Facebook option was turned off.
My eyes were fixed on VKontakte. Yes, it covers only Russia and the CIS (and unevenly in classmates, for example, the older public). Yes, there is a huge number of bots. VKontakte is not ideal, but it can distribute a list of friends in json-format through a request to al_friends.php.
')
But how to store and process this data?
After three days and a half terabyte of traffic, the friends database was received (by the way, only 22GB). And then the most interesting question arises: how to calculate the distance between users?
When solving resource-intensive tasks, I like to make such implementations that will work normally even on my modest netbook, and then turn on heavy artillery. As a heavy artillery, a modest server was used with two six-core Xeon X5650 and 32GB of memory. On it the distance was considered already for 10 seconds per stream. Taking into account parallelization, the distances between 144 pairs of users were calculated per minute.
Then began the strangeness with the data. Almost 50% of all users with a non-zero number of friends belonged to completely independent clusters in which there are no external links (or one and a half such links for the entire cluster). Roughly speaking, 50 people gave themselves to each other and nobody else. Pretty weird behavior, isn't it? Yes, it is possible that they are sectarians and religion forbids them to freel VKontakte non-sect members. But hardly, most likely these are bots.
Having thrown out bots caught in such an unexpected way, 6,773 user pairs were analyzed and a very interesting result was obtained:
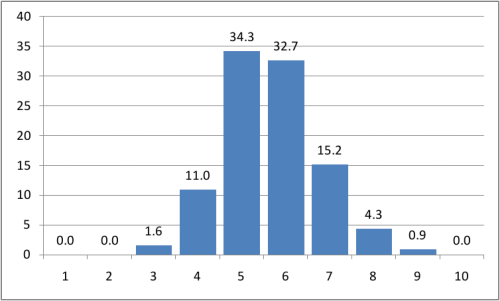
On the histogram on the x axis is the length of the shortest chain of friends found, and on the y axis is the probability of finding it in percent.
Thus, on average, there are 5.65 friends (i.e. 6.65 handshakes) between two random VKontakte users . This figure fits perfectly into the theory that is initially tested, and it also quite accurately coincides with the result obtained by Microsoft (they have released 6.6). So the result can be considered as another confirmation of the theory of six handshakes.
I really wanted to confirm this theory myself, using the data at hand - VKontakte. To translate my strange idea into reality, it was necessary to solve a whole range of problems:
- What data it all count on.
- Where is the data to take.
- How to save this data.
- What algorithm to use for calculations.
With the dominance of social networks in modern life, the question of where to get data on social relations is not so difficult. Of course, it would be great to take data about friends from Facebook, because it covers the whole world, and there are a lot of people there. But through a public API, I can’t pull out a friends list for any person, and parsing a page is not the most effective option, because Facebook spits out a list of friends in the form of dhtml, approximately 1kb of data per friend, for a total of 400M people * 130 friends on average * 1kb = 52 TB of traffic. Such a small amount of traffic did not fit into the research budget that was nulled to zero, and the Facebook option was turned off.
My eyes were fixed on VKontakte. Yes, it covers only Russia and the CIS (and unevenly in classmates, for example, the older public). Yes, there is a huge number of bots. VKontakte is not ideal, but it can distribute a list of friends in json-format through a request to al_friends.php.
')
But how to store and process this data?
- You can go to the forehead and write directly to MySQL: the spider spits out 100 users per second, each has 130 friends, for a total of 13,000 inserts into the database per second. The figure is not exorbitant, but given the fact that the spider worked on a weak server (the old single-core Athlone), it is not quite bright.
- You can write a text dump to disk, and then suck it into the database. In this scenario, the base will weigh approximately (4 bytes (user_id field size) + 4 bytes (friend_id field size) + 8 bytes per overhead and indices) * 80M VKontakte users * 130 friends = 166GB. Too much will be. Moreover, a sample from such a database of all the user's friends will not look like a super-efficient request.
- You can score on MySQL and use some hash-value storage. To write a couple of “user_id array (friend_id friend_id ...)” into it, this way the base will be blown away by a factor of four and all friends will be selected with a single disk access. Kyoto Cabinet was originally chosen as storage, but due to some strange performance anomalies on a large base, a move to the Google LevelDB took place.
After three days and a half terabyte of traffic, the friends database was received (by the way, only 22GB). And then the most interesting question arises: how to calculate the distance between users?
- The Floyd-Worshel algorithm would allow calculating distances from all users to all. A wonderful algorithm, but it has an unpleasant memory requirement - you need to store a square user_id / user_id matrix, which would occupy 1 byte * 80M users * 80M users = 6400 TB. Quite a bit too much.
- Dijkstra's algorithm would allow finding the distance from one user to all others at once. There are quite a few effective implementations of it, one of which was used for the sake of experiment. The algorithm worked wonderfully on a 1% synthetic sample of the entire base, but when it started up, on the average 10% of the base sample it began to severely slow down in a rather unexpected place - bypassing a large tree of friends constantly climbed to random memory locations and caught almost 100% of the CACHE_MISS of an already weak processor . Speaking in human terms, the data did not fit into the processor’s cache, and then the magical brakes began.
- Bidirectional search . Yes, not the most elegant algorithm in the world, but as simple as a multiplication table. Allows you to find the shortest distance between two users. Its implementation was written using bit fields, which were elegantly crammed into the processor's cache, as a result, the algorithm found the distance between two people in about half a minute.
When solving resource-intensive tasks, I like to make such implementations that will work normally even on my modest netbook, and then turn on heavy artillery. As a heavy artillery, a modest server was used with two six-core Xeon X5650 and 32GB of memory. On it the distance was considered already for 10 seconds per stream. Taking into account parallelization, the distances between 144 pairs of users were calculated per minute.
Then began the strangeness with the data. Almost 50% of all users with a non-zero number of friends belonged to completely independent clusters in which there are no external links (or one and a half such links for the entire cluster). Roughly speaking, 50 people gave themselves to each other and nobody else. Pretty weird behavior, isn't it? Yes, it is possible that they are sectarians and religion forbids them to freel VKontakte non-sect members. But hardly, most likely these are bots.
Having thrown out bots caught in such an unexpected way, 6,773 user pairs were analyzed and a very interesting result was obtained:

On the histogram on the x axis is the length of the shortest chain of friends found, and on the y axis is the probability of finding it in percent.
Thus, on average, there are 5.65 friends (i.e. 6.65 handshakes) between two random VKontakte users . This figure fits perfectly into the theory that is initially tested, and it also quite accurately coincides with the result obtained by Microsoft (they have released 6.6). So the result can be considered as another confirmation of the theory of six handshakes.
Source: https://habr.com/ru/post/132558/
All Articles