CPU
How much I remember myself, I always dreamed of making a processor. Finally, yesterday I made it. God knows that: 8 bits, RISC, the current operating frequency is 4 kHz, but it works. So far, in the logic circuit simulation program, but we all know: “today is on the model, tomorrow is in practice!”.
There are several animations under the cut, a brief introduction to the binary logic for the smallest ones, a short story about the main microchips of the processor logic and, in fact, a circuit.
The binary number system (for those who do not know) is a number system in which there are no numbers greater than one. This definition confuses many until they remember that there are no more than nine digits in the decimal notation.
The binary system is used in computers because the numbers in it are easy to encode with voltage: if there is voltage, it means unit; no voltage means zero. In addition, "zero" and "one" can easily be understood as "false" and "true." Moreover, most of the devices operating in the binary number system usually refer to numbers as an array of “truths” and “falsities”, that is, it operates with numbers as with logical quantities. For the smallest and those who do not know, I will tell and show you how the simplest elements of binary logic work.
')

Imagine you are sitting in your room, and your friend is in the kitchen. You shout to him: “Friend, tell me, is there a light in the corridor?”. A friend replies: "Yes, it burns!" Or "No, it does not burn." Your friend is the buffer between the signal source (a light bulb in the corridor) and the receiver (you). Moreover, your friend is not some kind of normal buffer, but a managed buffer. It would be a regular buffer if it constantly shouted: "The light is on" or "The light is off."

Now imagine that your friend is a joker who always tells a lie. And if the light in the corridor glows, then it will tell you "No, the corridor is very, very dark," and if it does not, then "Yes, the light is on in the corridor." If you really have such a friend, then he is the embodiment of the element "Not."
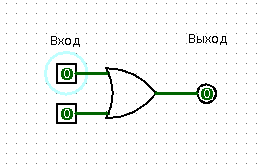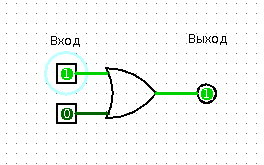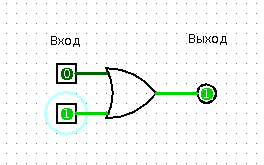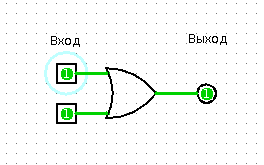
To explain the essence of the element "Or" one light bulb and one friend, unfortunately, is not enough. Need two light bulbs. So, you have two lights in the corridor - a floor lamp, for example, and a chandelier. You shout: “Friend, say, at least one light bulb in the corridor shines?”, And your friend answers “Yes” or “No”. Obviously, to answer "No" all the lights must be turned off.
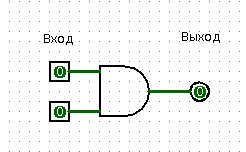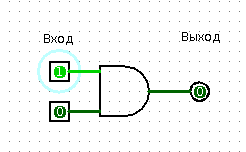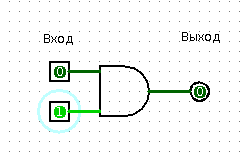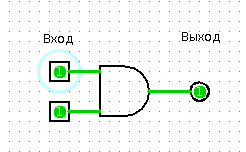
The same apartment, you, a friend in the kitchen, a floor lamp and a chandelier in the hallway. To your question “Is there both lights in the corridor?” You get the answer “Yes” or “No”. Congratulations, now your friend is an “AND” element.

We will repeat the experiment for the element “Or” once again, but we will reformulate our question to a friend: “Friend, tell me, is there only one light bulb in the corridor?”. An honest friend will answer this question “Yes” only if there is really only one light bulb in the corridor.

The quarter summator is called “Exclusive Or”. Why? Let's see.
Let's make the table of addition for two numbers in binary number system:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
Now we will write down the truth table of the “Exclusive Or” element. To do this, we denote the luminous light bulb as 1, the extinguished one as 0, and the answers of the friend “Yes” / “No” as 1 and 0, respectively.
0 xor 0 = 0
0 XOR 1 = 1
1 xor 0 = 1
1 XOR 1 = 0
Very similar, right? The addition table and the truth table of the “Exclusive Or” coincide completely, except for a single case. And this case is called "Overflow."
In case of overflow, the result of addition no longer fits into the same number of digits as the addends fit. The terms are two single digits (one significant digit, you understand?), And the sum is already two digits (two significant digits). Two digits with one light bulb (“Lit” / “Not lit”) cannot be transmitted. Need two light bulbs. Need to - do it!

In addition to XOR, for the adder, we need the element "AND" (AND).
0 XOR 0 = 0 0 AND 0 = 0
0 XOR 1 = 1 0 AND 1 = 0
1 XOR 0 = 1 1 AND 0 = 0
1 XOR 1 = 0 1 AND 1 = 1
Tadam!
0 + 0 = 00
0 + 1 = 01
1 + 0 = 01
1 + 1 = 10
Ourvundervaflya semi-adder works. It can be considered the simplest specialized processor that adds two numbers. A half-adder is called a half-adder because with its help the transfer (the result of the operation of another adder) cannot be taken into account, that is, you cannot add three single-digit binary numbers. In this regard, it is impossible to make one multi-digit one from several one-bit half-adders.
I will not go into the details of the work of full and multi-bit adders, just hope that you get the main idea.
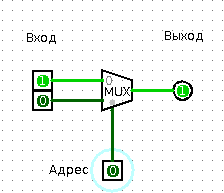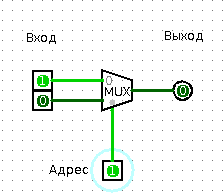
I propose to turn on the imagination. So imagine. You live in a private single-family house, your mailbox is near the door of this house. Going for a walk, you notice a strange postman, who stands near this very mailbox. And that's what he does: he takes a bunch of letters from his bag, reads the number on the mailbox, and, depending on the number on the box, throws one or another letter at him. The postman works as a multiplexer. He definitely (number on the envelope) determines which signal to send (letter) via the signal line (mailbox).
Multiplexers usually consist only of combinations of the elements "And", "Or" and "Not." In a single-bit multiplexer, one input is called “address selection”, two inputs with the common name “input signal” and one output, which is called: “output signal”.
When the “address selection” is 0, the “output signal” becomes the same as the first “input signal”. Accordingly, when the “choice” is fed 1, the “output signal” becomes equal to the second “input signal”.
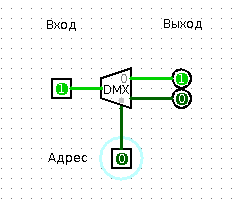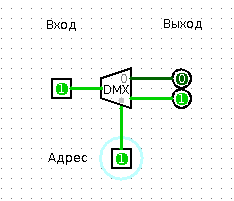
But this thing works exactly the opposite. We give the address to the “choice of address”, we give the data to the “data entry”, at the output with the number “address” we have the data from the input.
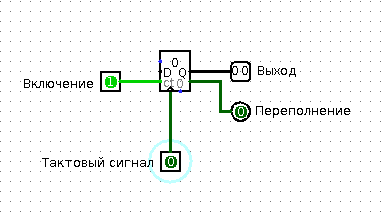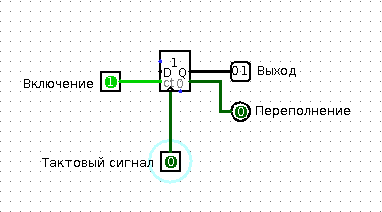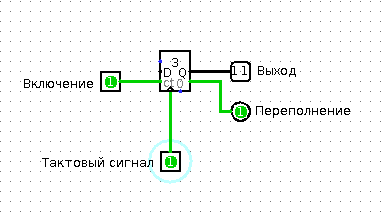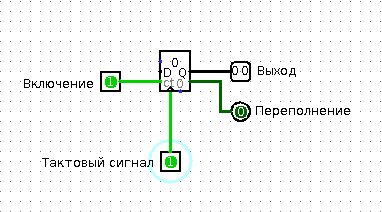
To understand the work of the counter, you will again need your friend. Call him out of the kitchen (I hope he didn’t miss him much, and, most importantly, he didn’t eat all your food), and ask him to do this: let him remember the number 0. Every time you touch him, he should add one to the number that remembers, say the result and remember it. When the result is equal to (let's say) 3, he should shout out “Abracadabra!” And answer with the next touch that he now remembers the number 0. Is it a bit difficult? See:
You are touching a friend. A friend says "One."
You are touching a friend. A friend says "Two."
You are touching a friend. A friend says "Three." A friend shouts out “ Habrahabr! ".Critical attack! You are temporarily paralyzed and cannot move.
You are touching a friend. A friend says "Zero."
Well, and so on. Very simple, right?
Of course, you realized that your friend is now a counter. Touching a friend can be considered a “clocking signal” or, quite simply, a signal to continue counting. The cry “Abracadabra” indicates that the memorized value in the counter is maximum, and that with the next clocking signal the counter will be set to zero. There are two differences between a binary counter and your friend. First: a real binary counter gives the memorized value in binary form. Second: he always does only what you tell him, and never descends into silly jokes that can disrupt the work of the entire processor system.

Let's continue to mock your unfortunate (perhaps even imaginary) friend. Let him now remember the number zero. When you touch his left hand, he must memorize the number zero, and when the right hand - the number one. When asking the question “What number do you remember?” A friend should always answer the number that he memorized - zero or one.
The simplest storage cell is the RS trigger (“trigger” means “switch”). An RS trigger can store one data bit (“zero” / “one”), and has two inputs. The Set / Setup input (just like your friend’s left hand) records a “one” trigger and the Reset / Reset input (respectively, the right hand) a “zero”.

The register is slightly more complex. Your friend turns into a register when you ask him to remember something, and then say, “Hey, remind me, what did I tell you to remember?”, And the friend answers correctly.
The register can usually store a bit more than one bit. It must have a data input, data output and write enable input. From the release of the data you can read at any time what is written in this register. At the input of the data you can submit the data that you want in this register to write. You can submit data until you get bored. Anyway, nothing will be written to the register until you submit one, that is, a “logical unit” to the recording permission input.
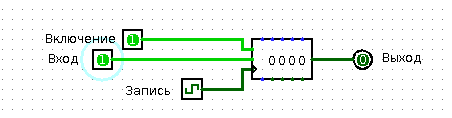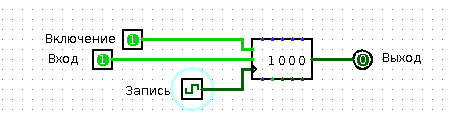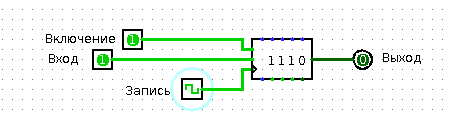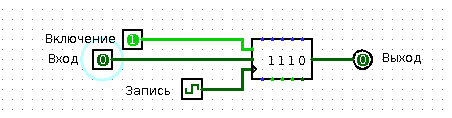
Have you ever stood in line? Surely they were. So you imagine what it is to be data in a shift register. People come and go to the end of the line. The first person in the queue enters the office at a big shot. The one who was second in the queue becomes the first, and the one who was third is now the second, and so on. A queue is such a tricky shift register from which “data” (well, that is, people) can run away on business, after having warned neighbors in turn. In the present shift register, of course, the “data” from the queue cannot escape.
So, the shift register has a data input (through which data enters the “queue”) and a data output (from which the very first entry in the “queue” can be read). Even the shift register has an input “shift register”. As soon as a “logical unit” arrives at this input, the entire queue shifts.
There is one important difference between a queue and a shift register. If the shift register is designed for four entries (for example, four bytes), then the first entry in the queue will reach the exit from the register only after four signals to the “shift register” input.
If many-many triggers are combined into registers, and many-many registers are combined in one chip, then you get a memory chip. A memory chip usually has an address input, bidirectional data input (that is, it can be written to this input and can also be read from it) and a write enable input. At the input of the address, we submit some number, and this number will select a specific memory cell. After that, the input / output data, we can read what is written in this very cell.
Now we will simultaneously submit to the input / output of the data that we want to write to this cell, and to the input of the recording resolution - “logical unit”. The result is a bit predictable, isn't it?
Processors are sometimes divided into CISCs - those that can perform many different commands, and RISCs - those that can perform few commands, but perform them well. One fine evening, I thought: it would be great if you could make a full-fledged processor that can perform only one command. I soon learned that there is a whole class of single-processor processors - OISC, most often they use the Subleq command (subtract, and if it is less or equal to zero, then go) or Subeq (subtract, and if it is zero, then go). Studying various variants of OISC-processors, I found Oleg Mazakovka’s website, which developed the simplest single-command language BitBitJump. The only command of this language is called BitBitJump (copy a bit and go to the address). This, of course, esoteric, language is Turing complete — that is, any computer algorithm can be implemented on it.
A detailed description of BitBitJump and assembler for this language can be found on the developer’s website . To describe the algorithm of the processor is enough to know the following:
1. When turning on the processor in the registers PC, A and B are written 0
2. Read the memory cell with the PC address and save the read in register A
3. Increase PC
4. Read the memory cell with the PC address and save the read in register B
5. Increase PC
6. Write to the cell with the address recorded in the register B, the contents of the bit with the address A.
7. Read the memory cell with the address of the PC and save the read in register B
8. Write to the PC register the contents of register B
9. Go to paragraph 2 of our plan.
10. PROFIT !!!
Unfortunately, the algorithm is infinite, and therefore PROFIT will not be achieved.
The scheme was built spontaneously, so fear, horror and confusion reign in it. However, it works, and works decently. To turn on the processor, you need:
1. Enter the program into RAM
2. Press the switch
3. Set the counter to position 4 (this can be done in hardware, but the circuit would become even more cumbersome)
4. Turn on the clock generator
As you can see, one register, one shift register, one RAM chip, two binary counters, one demultiplexer (represented by comparators), two multiplexers and some pure logic are used.

You can download the circ format for the Logisim program, and play around.
First, you can increase the processor's bit depth - by replacing 8-bit elements with 16-bit elements.
Secondly, you can remove the RAM from the processor, and add a simple circuit that will pause the processor, change the RAM and turn on the processor again. This scheme will perform the functions of a simple I / O controller. Then it will be possible to make a calculator, controller, or some other funny useless thing based on this processor.
Thirdly, it is possible to embody all this scheme in the gland. What am I going to do. As soon as I do, I will definitely tell and show.
Thank you all for your attention!
PS Links (for those who are too lazy to read):
1. URISC processors - en.wikipedia.org/wiki/Urisc
2. BitBitJump language site - mazonka.com/bbj/index.html
3. A program for modeling Logisim logic schemes - http://ozark.hendrix.edu/~burch/logisim/
4. Self-made URISC (ORISC) processor for Logisim - narod.ru/disk/31367690001/oo.circ.html
There are several animations under the cut, a brief introduction to the binary logic for the smallest ones, a short story about the main microchips of the processor logic and, in fact, a circuit.
Binary logic
The binary number system (for those who do not know) is a number system in which there are no numbers greater than one. This definition confuses many until they remember that there are no more than nine digits in the decimal notation.
The binary system is used in computers because the numbers in it are easy to encode with voltage: if there is voltage, it means unit; no voltage means zero. In addition, "zero" and "one" can easily be understood as "false" and "true." Moreover, most of the devices operating in the binary number system usually refer to numbers as an array of “truths” and “falsities”, that is, it operates with numbers as with logical quantities. For the smallest and those who do not know, I will tell and show you how the simplest elements of binary logic work.
')
Buffer Element

Imagine you are sitting in your room, and your friend is in the kitchen. You shout to him: “Friend, tell me, is there a light in the corridor?”. A friend replies: "Yes, it burns!" Or "No, it does not burn." Your friend is the buffer between the signal source (a light bulb in the corridor) and the receiver (you). Moreover, your friend is not some kind of normal buffer, but a managed buffer. It would be a regular buffer if it constantly shouted: "The light is on" or "The light is off."
Element NOT - NOT

Now imagine that your friend is a joker who always tells a lie. And if the light in the corridor glows, then it will tell you "No, the corridor is very, very dark," and if it does not, then "Yes, the light is on in the corridor." If you really have such a friend, then he is the embodiment of the element "Not."
Element "Or" - OR

To explain the essence of the element "Or" one light bulb and one friend, unfortunately, is not enough. Need two light bulbs. So, you have two lights in the corridor - a floor lamp, for example, and a chandelier. You shout: “Friend, say, at least one light bulb in the corridor shines?”, And your friend answers “Yes” or “No”. Obviously, to answer "No" all the lights must be turned off.
Element "And" - AND

The same apartment, you, a friend in the kitchen, a floor lamp and a chandelier in the hallway. To your question “Is there both lights in the corridor?” You get the answer “Yes” or “No”. Congratulations, now your friend is an “AND” element.
Exclusive Or Element - XOR

We will repeat the experiment for the element “Or” once again, but we will reformulate our question to a friend: “Friend, tell me, is there only one light bulb in the corridor?”. An honest friend will answer this question “Yes” only if there is really only one light bulb in the corridor.
Adders
Quarter summator

The quarter summator is called “Exclusive Or”. Why? Let's see.
Let's make the table of addition for two numbers in binary number system:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
Now we will write down the truth table of the “Exclusive Or” element. To do this, we denote the luminous light bulb as 1, the extinguished one as 0, and the answers of the friend “Yes” / “No” as 1 and 0, respectively.
0 xor 0 = 0
0 XOR 1 = 1
1 xor 0 = 1
1 XOR 1 = 0
Very similar, right? The addition table and the truth table of the “Exclusive Or” coincide completely, except for a single case. And this case is called "Overflow."
Semi-adder
In case of overflow, the result of addition no longer fits into the same number of digits as the addends fit. The terms are two single digits (one significant digit, you understand?), And the sum is already two digits (two significant digits). Two digits with one light bulb (“Lit” / “Not lit”) cannot be transmitted. Need two light bulbs. Need to - do it!

In addition to XOR, for the adder, we need the element "AND" (AND).
0 XOR 0 = 0 0 AND 0 = 0
0 XOR 1 = 1 0 AND 1 = 0
1 XOR 0 = 1 1 AND 0 = 0
1 XOR 1 = 0 1 AND 1 = 1
Tadam!
0 + 0 = 00
0 + 1 = 01
1 + 0 = 01
1 + 1 = 10
Our
I will not go into the details of the work of full and multi-bit adders, just hope that you get the main idea.
More complex items
Multiplexer

I propose to turn on the imagination. So imagine. You live in a private single-family house, your mailbox is near the door of this house. Going for a walk, you notice a strange postman, who stands near this very mailbox. And that's what he does: he takes a bunch of letters from his bag, reads the number on the mailbox, and, depending on the number on the box, throws one or another letter at him. The postman works as a multiplexer. He definitely (number on the envelope) determines which signal to send (letter) via the signal line (mailbox).
Multiplexers usually consist only of combinations of the elements "And", "Or" and "Not." In a single-bit multiplexer, one input is called “address selection”, two inputs with the common name “input signal” and one output, which is called: “output signal”.
When the “address selection” is 0, the “output signal” becomes the same as the first “input signal”. Accordingly, when the “choice” is fed 1, the “output signal” becomes equal to the second “input signal”.
Demultiplexer

But this thing works exactly the opposite. We give the address to the “choice of address”, we give the data to the “data entry”, at the output with the number “address” we have the data from the input.
Counter

To understand the work of the counter, you will again need your friend. Call him out of the kitchen (I hope he didn’t miss him much, and, most importantly, he didn’t eat all your food), and ask him to do this: let him remember the number 0. Every time you touch him, he should add one to the number that remembers, say the result and remember it. When the result is equal to (let's say) 3, he should shout out “Abracadabra!” And answer with the next touch that he now remembers the number 0. Is it a bit difficult? See:
You are touching a friend. A friend says "One."
You are touching a friend. A friend says "Two."
You are touching a friend. A friend says "Three." A friend shouts out “ Habrahabr! ".
You are touching a friend. A friend says "Zero."
Well, and so on. Very simple, right?
Of course, you realized that your friend is now a counter. Touching a friend can be considered a “clocking signal” or, quite simply, a signal to continue counting. The cry “Abracadabra” indicates that the memorized value in the counter is maximum, and that with the next clocking signal the counter will be set to zero. There are two differences between a binary counter and your friend. First: a real binary counter gives the memorized value in binary form. Second: he always does only what you tell him, and never descends into silly jokes that can disrupt the work of the entire processor system.
Memory
Trigger

Let's continue to mock your unfortunate (perhaps even imaginary) friend. Let him now remember the number zero. When you touch his left hand, he must memorize the number zero, and when the right hand - the number one. When asking the question “What number do you remember?” A friend should always answer the number that he memorized - zero or one.
The simplest storage cell is the RS trigger (“trigger” means “switch”). An RS trigger can store one data bit (“zero” / “one”), and has two inputs. The Set / Setup input (just like your friend’s left hand) records a “one” trigger and the Reset / Reset input (respectively, the right hand) a “zero”.
Register

The register is slightly more complex. Your friend turns into a register when you ask him to remember something, and then say, “Hey, remind me, what did I tell you to remember?”, And the friend answers correctly.
The register can usually store a bit more than one bit. It must have a data input, data output and write enable input. From the release of the data you can read at any time what is written in this register. At the input of the data you can submit the data that you want in this register to write. You can submit data until you get bored. Anyway, nothing will be written to the register until you submit one, that is, a “logical unit” to the recording permission input.
Shift register

Have you ever stood in line? Surely they were. So you imagine what it is to be data in a shift register. People come and go to the end of the line. The first person in the queue enters the office at a big shot. The one who was second in the queue becomes the first, and the one who was third is now the second, and so on. A queue is such a tricky shift register from which “data” (well, that is, people) can run away on business, after having warned neighbors in turn. In the present shift register, of course, the “data” from the queue cannot escape.
So, the shift register has a data input (through which data enters the “queue”) and a data output (from which the very first entry in the “queue” can be read). Even the shift register has an input “shift register”. As soon as a “logical unit” arrives at this input, the entire queue shifts.
There is one important difference between a queue and a shift register. If the shift register is designed for four entries (for example, four bytes), then the first entry in the queue will reach the exit from the register only after four signals to the “shift register” input.
RAM
If many-many triggers are combined into registers, and many-many registers are combined in one chip, then you get a memory chip. A memory chip usually has an address input, bidirectional data input (that is, it can be written to this input and can also be read from it) and a write enable input. At the input of the address, we submit some number, and this number will select a specific memory cell. After that, the input / output data, we can read what is written in this very cell.
Now we will simultaneously submit to the input / output of the data that we want to write to this cell, and to the input of the recording resolution - “logical unit”. The result is a bit predictable, isn't it?
CPU
Bitbitjump
Processors are sometimes divided into CISCs - those that can perform many different commands, and RISCs - those that can perform few commands, but perform them well. One fine evening, I thought: it would be great if you could make a full-fledged processor that can perform only one command. I soon learned that there is a whole class of single-processor processors - OISC, most often they use the Subleq command (subtract, and if it is less or equal to zero, then go) or Subeq (subtract, and if it is zero, then go). Studying various variants of OISC-processors, I found Oleg Mazakovka’s website, which developed the simplest single-command language BitBitJump. The only command of this language is called BitBitJump (copy a bit and go to the address). This, of course, esoteric, language is Turing complete — that is, any computer algorithm can be implemented on it.
A detailed description of BitBitJump and assembler for this language can be found on the developer’s website . To describe the algorithm of the processor is enough to know the following:
1. When turning on the processor in the registers PC, A and B are written 0
2. Read the memory cell with the PC address and save the read in register A
3. Increase PC
4. Read the memory cell with the PC address and save the read in register B
5. Increase PC
6. Write to the cell with the address recorded in the register B, the contents of the bit with the address A.
7. Read the memory cell with the address of the PC and save the read in register B
8. Write to the PC register the contents of register B
9. Go to paragraph 2 of our plan.
Unfortunately, the algorithm is infinite, and therefore PROFIT will not be achieved.
Actually, the scheme
The scheme was built spontaneously, so fear, horror and confusion reign in it. However, it works, and works decently. To turn on the processor, you need:
1. Enter the program into RAM
2. Press the switch
3. Set the counter to position 4 (this can be done in hardware, but the circuit would become even more cumbersome)
4. Turn on the clock generator
As you can see, one register, one shift register, one RAM chip, two binary counters, one demultiplexer (represented by comparators), two multiplexers and some pure logic are used.

You can download the circ format for the Logisim program, and play around.
What's next?
First, you can increase the processor's bit depth - by replacing 8-bit elements with 16-bit elements.
Secondly, you can remove the RAM from the processor, and add a simple circuit that will pause the processor, change the RAM and turn on the processor again. This scheme will perform the functions of a simple I / O controller. Then it will be possible to make a calculator, controller, or some other funny useless thing based on this processor.
Thirdly, it is possible to embody all this scheme in the gland. What am I going to do. As soon as I do, I will definitely tell and show.
Thank you all for your attention!
PS Links (for those who are too lazy to read):
1. URISC processors - en.wikipedia.org/wiki/Urisc
2. BitBitJump language site - mazonka.com/bbj/index.html
3. A program for modeling Logisim logic schemes - http://ozark.hendrix.edu/~burch/logisim/
4. Self-made URISC (ORISC) processor for Logisim - narod.ru/disk/31367690001/oo.circ.html
Source: https://habr.com/ru/post/132486/
All Articles