Happy Toolers - Mathematics on the nose

Search for happiness is useless, the main thing is where it will find you. Some, including myself, have got the habit of checking route tickets for this “happiness” - a ticket can be called “happy” if the sum of its first three digits is equal to the sum of the other three. Funny is, you know, occupation.

But sometimes it happens that happy tickets come across very often, and sometimes - they do not happen for several months. This is if you go once a day along some route.

And here comes the wonderful question: “how many happy tickets there are?”, And even better, when mathematics comes with its equally beautiful question: “What is the probability of buying a happy ticket?”

For a person who has comprehended the basics of programming, it will not be difficult to write a program to count this same number of lucky tickets - the usual method of enumeration. What I did, having received the result - 55 251 tickets, which says that approximately every eighteenth ticket will be happy.
')
But now imagine the image of the conductor - a man-bag-through neck, with a few kilograms of fines and a coil of tickets, which he gives out consistently for a certain fee. And what will happen if you become a happy owner of a ticket with the number "010100"? That's right, there will be no happy travelers on this route until the conductor finishes with this coil.

Now we will try to answer this question mathematically.

The maximum possible lucky ticket "999999" has the sum of triads equal to 27 = 9 + 9 + 9 = 9 + 9 + 9. Tickets with the amount of lucky numbers equal to 1 will be 9, these are tickets:

001001 010001 100001
001010 010010 100010
001100 010100 100100

Tickets with the sum of lucky numbers equal to 3 will be 36. You can count it yourself - by any method. Create a table for each such combination:

Triad Amount / Number of lucky tickets in a group
nineteen
2/36
3/100
4/225
5/441
6/784
7/1296
8/2025
9/3025
10/3969
11/4761
12/5329
13/5625
14/5625
15/5329
16/4761
17/3969
18/3025
19/2025
20/1296
21/784
22/441
23/225
24/100
25/36
26/9
27/1
Amount: 55251

It turns out that the maximum number of lucky tickets will be in groups, the sum of the triads of which is 13 or 14.


In such coils, every ninth ticket will be happy until the sum of two digits of one triad exceeds the value of 13 ... 14. Therefore, it can be logically assumed that every 18 tickets in such a group will be happy. And in view of this “classic” distribution, it is in the whole group of tickets from 000001 to 999999.

It remains to recall one of the methods of the theory of probability, and calculate:


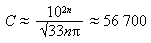
Getting the result with good accuracy, with a deviation of ≈ 3%.

And still, happy tickets need to be eaten to feel this tide of universal happiness.

Be happy!