Algorithms used in data compression

Introduction

One of the most important problems when working with data is their size. We always want to fit as much as possible. But sometimes this is not done. Therefore, various archivers come to the rescue. But how do they compress the data? I will not write about the principle of their work, just talk about a few compression algorithms that they use.

Huffman Algorithm

Codes or Huffman codes (Huffman codes) - a widespread and very effective method of data compression, which, depending on the characteristics of these data, usually saves from 20% to 90% of the volume.
We consider the data, which is a sequence of characters. The greedy Huffman algorithm uses a table containing the frequency of occurrence of certain characters. This table is used to determine the optimal representation of each character as a binary string.

Code building

The basis of the Huffman algorithm is the idea: to encode more shortly those characters that are more common, and those that are less common to encode longer. To build a Huffman code, we need a symbol frequency table. Consider an example of building code on a simple abacaba line.

• abc
• 4 2 1

Process b and c

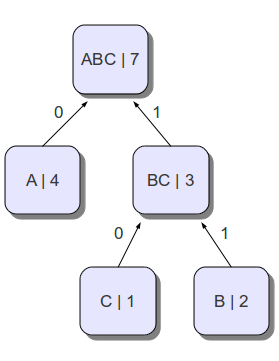
The next step is to build a tree, where the vertices are “characters”, and the paths to them correspond to their prefix codes. To do this, at each step we will take two symbols with a minimum frequency of entry, and combine them into new so-called symbols with a frequency equal to the sum of the frequencies of those we combined, and also connect them with edges, thus forming a tree (see figure). Choose the minimum two characters will be from all the characters, excluding those that we have already chosen. In the example, we combine the symbols b and c into the symbol bc with frequency 3. Then we combine a and bc into the symbol abc, thereby obtaining a tree. Now the paths from the root (abc) to the leaves are Huffman Codes (each edge corresponds to either 1 or 0)

• abc
• 0 11 10

The resulting tree

')

MTF conversion

MTF (move-to-front, go-ahead) is a coding algorithm used for preprocessing data (usually a stream of bytes) before compression, designed to improve the performance of subsequent coding.

Code building

Initially, each possible value of a byte is written into a list (alphabet), into a cell with a number equal to the value of a byte, i.e. (0, 1, 2, 3, ..., 255). In the course of data processing this list changes. As the next character arrives, the number of the element containing its value is output. Then this symbol moves to the beginning of the list, shifting the remaining elements to the right.
Modern algorithms (for example, bzip2) before the MTF algorithm use the BWT algorithm, therefore, as an example, consider the string s = “BCABAAA”, obtained from the string “ABACABA” as a result of the Burrows-Wheeler transformation (more on this later). The first character of the string s = 'B' is the second element of the alphabet “ABC”, so the output is 1. After moving 'B' to the beginning of the alphabet, it becomes “BAC”. Further work of the algorithm:

• Symbol List Output
• B ABC 1
• C BAC 2
• A CBA 2
• B ACB 2
• A BAC 1
• A ABC 0
• A ABC 0

Thus, the result of the algorithm MTF (s): "1222100".

Inverse transform

Let the string s = "1222100" and the source alphabet "ABC" be given. The character with number 1 in the alphabet is 'B'. The output is 'B', and this character moves to the beginning of the alphabet. The character number 2 in the alphabet is 'A', so 'A' is fed to the output and moved to the beginning of the alphabet. Further conversion occurs similarly.

• Symbol List Output
• 1 ABC B
• 2 BAC C
• 2 CBA A
• 2 ACB B
• 1 BAC A
• 0 ABC A
• 0 ABC A

Hence, the source string s = "BCABAAA".

Burrows-Wheeler Transformation

Burrows-Wheeler transform (Burrows-Wheeler transform, BWT) is an algorithm used in data compression techniques to transform raw data.
Bzip2 uses the Burrows-Wheeler transform to turn sequences of repeatedly alternating characters into strings of the same characters, then applies the MTF transform, and at the end Huffman coding.

Algorithm operation

The conversion is performed in three stages. At the first stage, a table is created of all cyclic shifts of the input line. At the second stage, the lexicographic (in alphabetical order) sorting of the rows of the table is performed. At the third stage, the last column of the conversion table is selected as the output row. The following example illustrates the described algorithm:
Let us be given the source string s = "ABACABA".

The result is briefly written as: BWT (s) = (“BCABAAA”, 3), where 3 is the number of the original row in the sorted matrix, as it may be needed for the inverse transformation.
It should be noted that sometimes the source line contains the so-called end-of-line character $, which in the conversion will be considered the last character, then saving the number of the original line is not required. With the same transformation as above, that line in the matrix that will end with the end of line character will be the original (“ABACABA $”). In this case, when sorting the matrix, this symbol will be considered as the last after all the characters of the alphabet. Then the result can be written as BWT (s) = "$ CBBAAAA". It will be equivalent to the first, since it also contains all the characters in the source string.

Inverse transform

Let us be given: BWT (s) = (“BCABAAA”, 3). Then write down our converted character sequence “BCABAAA” in the column. We write it as the last column of the previous matrix (with the direct Burrows – Wheeler transformation), while leaving all the previous columns empty. Next, sort the matrix line by line, then in the previous column we write "BCABAAA". Again, sort the matrix line by line. Continuing in this way, you can restore a complete list of all the cyclic permutations of the string that we need to find. Having built a complete sorted list of permutations, select the line with the number that was originally given to us. As a result, we get the desired string. The inverse transform algorithm is described in the table below:

It should also be noted that if we were given BWT (s) = "$ CBBAAAA", we would also receive our original string, only with the end-of-line character $ at the end: ABACABA $.

Conclusion

These three algorithms are used in our time in the bzip2 utility for data compression. But not only because these algorithms are very effective in their work.