Interpolation: draw smooth graphics with PHP and GD
A common task for a programmer is to draw graphs. The input is an array of points (x i ; y i ). As a rule, we know only some values - in certain points of the graph. To build a continuous curve curve, you must resort to interpolation or approximation .

Interpolation is the construction of a curve passing through given points.
Approximation - approximation of the curve to the original, but not necessarily passing through the specified points.
')
In this topic, I want to demonstrate my library for PHP, which interpolates using the Lagrange polynomial, C-spline and Akima spline, as well as the Bezier curve approximation. Additionally, it implements segment drawing with anti-aliasing.
Briefly consider the methods of interpolation and approximation.
The first thing that comes to mind is to connect the points with segments:
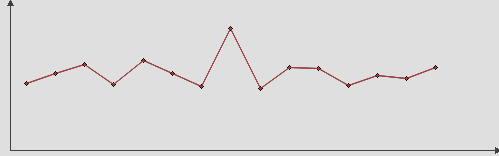
The best solution for speed, but the resulting graph is broken - this is not what we need.
A polynomial of degree n for n + 1 points. Its formula is quite simple:

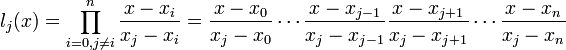
It is simple to implement, but it has two serious drawbacks:
1) requires a significant amount of computation
2) behaves unpredictably between given points (nodes)

The cubic spline is devoid of the disadvantages of the previous method. For each interval between nodes, a polynomial of degree at most 3 is specified; the first and second derivatives of the function must be continuous. This, on the one hand, simplifies calculations, and on the other, it allows one to avoid sharp jumps in curvature.
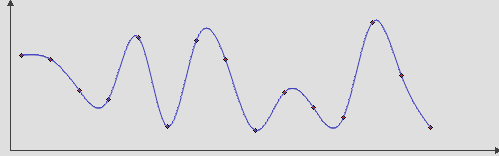
I ported the implementation of the cubic spline from the C # code taken from Wikipedia .
Cubic splines have a drawback: in the area far from their neighbors, such splines can make unexpected “spikes”. This problem can be solved using the splines proposed by Hiroshi Akim. Please note - Akim's spline is more stable:

I ported the implementation of Akim's spline from the C-code of the program for debian aspline David Frey .
Sometimes it is useful not to draw a curve through given points, but to use them as reference points. The Bezier curve method will help us in this (I ported the code from Tolga Birdal’s C # example ). The curve passes through the first and last points.

Conducted for the 500x500 size chart without rendering on the Xeon 5560 2.8GHz server, the number of experiments = 1000. Average execution time, with:
From the table below we can draw the following conclusions:
1) The calculation time of the Lagrange polynomial is rapidly increasing with increasing number of points.
2) Akima spline runs faster than cubic.
3) Construction of the Bezier curve slower splines.
First, think: Do you need to hold the curve between the points at all? If there are few points, it may be better to use a table? If you are dealing with statistical data on grouping ranges (for example, the average temperature by months over many years of data), then it is better to use a histogram.
If you need to draw a curve through known points, I would recommend using Akima spline. If the points themselves do not play a big role, then I would approximate the graph of the Bezier curve.
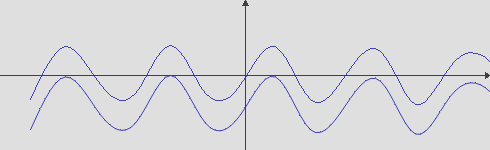
The construction of the curve in the library gd can be done by segments. For this, the curve is divided into sections with a certain step (at least 1 pixel) and between the beginning and the end of the section we draw a line with the imageline function. However, this segment of PHP will draw without anti-aliasing. An algorithm for drawing a segment with screen antialiasing - Wu's algorithm - comes to the rescue. The Wu algorithm can draw only segments at an angle of ± 45 °, so in other cases it has to be “rotated”. The figure shows a graph of the function sin (x) without anti-aliasing, and below nothing with anti-aliasing.
For each interpolation / approximation method I wrote a separate class: LagrangePolynomial, CubicSpline, AkimaSpline, BezierCurve. Each class has 3 public methods:
setCoords (& coordinates, step, [x_min, [x_max]]) - sets the initial coordinates and parameters of the curve, returns false in case of an error
process () - returns an array of coordinates to construct a curve
getError () - returns an error message
Coordinates are transmitted in the form of an array (x1 => y1, x2 => y2 ... xn => yn)
For plotting, auxiliary class Plot is implemented. Its capabilities are very modest (for example, there is no scaling - the graph is built 1: 1), so instead of it you can use another class or native PHP functions. Methods:
The constructor receives an array of coordinates.
drawLine (image, color, [x0, [y0]]) - draws a broken line, image - resource identifier, color should be set to imagecolorallocate, x0 and y0 - offset of the origin (by default - in the lower left corner of the image)
drawAALine (image, color, [x0, [y0]]) - draws a broken line with anti-aliasing of segments, parameters similar to drawLine
drawDots (image, color, [x0, [y0, [size]]]) - draws points without joints, segments like drawLine, size - diameter of dots
drawAxis (image, color, [x0, [y0, [1kv]]]) draws axes, parameters are similar to drawLine, if 1kv = true (default), axes are drawn only for the first quadrant - in the positive direction
Example (sin (x) function):
Download library and demo version
E.P. Kuzmin, D.V. Ivanov Algorithmic Basics of Computer Graphics (Lecture No. 4)
Spline Interpolation
Original article Akims
Comparison of cubic and Akima spline
Bezier Curves Made Simple
Wikipedia:
Lagrange polynomial .
Cubic spline
Bezier curves

Interpolation is the construction of a curve passing through given points.
Approximation - approximation of the curve to the original, but not necessarily passing through the specified points.
')
In this topic, I want to demonstrate my library for PHP, which interpolates using the Lagrange polynomial, C-spline and Akima spline, as well as the Bezier curve approximation. Additionally, it implements segment drawing with anti-aliasing.
Briefly consider the methods of interpolation and approximation.
Piecewise linear interpolation
The first thing that comes to mind is to connect the points with segments:

The best solution for speed, but the resulting graph is broken - this is not what we need.
Interpolation Lagrange Polynomial
A polynomial of degree n for n + 1 points. Its formula is quite simple:

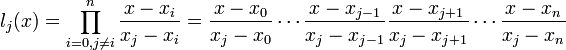
It is simple to implement, but it has two serious drawbacks:
1) requires a significant amount of computation
2) behaves unpredictably between given points (nodes)

Cubic spline (c-spline)
The cubic spline is devoid of the disadvantages of the previous method. For each interval between nodes, a polynomial of degree at most 3 is specified; the first and second derivatives of the function must be continuous. This, on the one hand, simplifies calculations, and on the other, it allows one to avoid sharp jumps in curvature.

I ported the implementation of the cubic spline from the C # code taken from Wikipedia .
Spline Akims
Cubic splines have a drawback: in the area far from their neighbors, such splines can make unexpected “spikes”. This problem can be solved using the splines proposed by Hiroshi Akim. Please note - Akim's spline is more stable:

I ported the implementation of Akim's spline from the C-code of the program for debian aspline David Frey .
Bézier curve approximation
Sometimes it is useful not to draw a curve through given points, but to use them as reference points. The Bezier curve method will help us in this (I ported the code from Tolga Birdal’s C # example ). The curve passes through the first and last points.

Performance testing
Conducted for the 500x500 size chart without rendering on the Xeon 5560 2.8GHz server, the number of experiments = 1000. Average execution time, with:
| Number of points: | five | 15 | 50 |
| Lagrange polynomial | 1.789 | 5.664 | 20.446 |
| Cubic spline | 0.153 | 0.230 | 0.313 |
| Spline Akims | 0.017 | 0.024 | 0.049 |
| Bezier curve | 0.244 | 0.276 | 0.304 |
From the table below we can draw the following conclusions:
1) The calculation time of the Lagrange polynomial is rapidly increasing with increasing number of points.
2) Akima spline runs faster than cubic.
3) Construction of the Bezier curve slower splines.
Method selection
First, think: Do you need to hold the curve between the points at all? If there are few points, it may be better to use a table? If you are dealing with statistical data on grouping ranges (for example, the average temperature by months over many years of data), then it is better to use a histogram.
If you need to draw a curve through known points, I would recommend using Akima spline. If the points themselves do not play a big role, then I would approximate the graph of the Bezier curve.
Anti-aliasing
The construction of the curve in the library gd can be done by segments. For this, the curve is divided into sections with a certain step (at least 1 pixel) and between the beginning and the end of the section we draw a line with the imageline function. However, this segment of PHP will draw without anti-aliasing. An algorithm for drawing a segment with screen antialiasing - Wu's algorithm - comes to the rescue. The Wu algorithm can draw only segments at an angle of ± 45 °, so in other cases it has to be “rotated”. The figure shows a graph of the function sin (x) without anti-aliasing, and below nothing with anti-aliasing.

Library
For each interpolation / approximation method I wrote a separate class: LagrangePolynomial, CubicSpline, AkimaSpline, BezierCurve. Each class has 3 public methods:
setCoords (& coordinates, step, [x_min, [x_max]]) - sets the initial coordinates and parameters of the curve, returns false in case of an error
process () - returns an array of coordinates to construct a curve
getError () - returns an error message
Coordinates are transmitted in the form of an array (x1 => y1, x2 => y2 ... xn => yn)
For plotting, auxiliary class Plot is implemented. Its capabilities are very modest (for example, there is no scaling - the graph is built 1: 1), so instead of it you can use another class or native PHP functions. Methods:
The constructor receives an array of coordinates.
drawLine (image, color, [x0, [y0]]) - draws a broken line, image - resource identifier, color should be set to imagecolorallocate, x0 and y0 - offset of the origin (by default - in the lower left corner of the image)
drawAALine (image, color, [x0, [y0]]) - draws a broken line with anti-aliasing of segments, parameters similar to drawLine
drawDots (image, color, [x0, [y0, [size]]]) - draws points without joints, segments like drawLine, size - diameter of dots
drawAxis (image, color, [x0, [y0, [1kv]]]) draws axes, parameters are similar to drawLine, if 1kv = true (default), axes are drawn only for the first quadrant - in the positive direction
Example (sin (x) function):
<? php
// For convenience, set the size in advance
define ( 'GRAPH_WIDTH' , 490 ) ;
define ( 'GRAPH_HEIGHT' , 150 ) ;
// General SmoothCurve abstract class
include_once ( 'SmoothCurve.class.php' ) ;
// Cubic Spline Class
include_once ( 'CubicSpline.class.php' ) ;
// You can also use
// include_once ('AkimaSpline.class.php');
// include_once ('BezierCurve.class.php');
// Helper class for drawing graphs
// You can use your own or native PHP functions instead
include_once ( 'Plot.class.php' ) ;
// Set the coordinates in the array array (x1 => y1, x2 => y2 ... xn => yn)
$ testCoords [ - 215 ] = - 24.2705098312 ;
$ testCoords [ - 180 ] = 28.5316954889 ;
$ testCoords [ - 145 ] = - 9.27050983125 ;
$ testCoords [ - 110 ] = - 17.6335575688 ;
$ testCoords [ - 75 ] = 30 ;
$ testCoords [ - 40 ] = - 17.6335575688 ;
$ testCoords [ - 5 ] = - 9.27050983125 ;
$ testCoords [ 30 ] = 28.5316954889 ;
$ testCoords [ 65 ] = - 24.2705098312 ;
$ testCoords [ 100 ] = 0 ;
$ testCoords [ 135 ] = 24.2705098312 ;
$ testCoords [ 170 ] = - 28.5316954889 ;
$ testCoords [ 205 ] = 9.27050983125 ;
$ testCoords [ 240 ] = 17.6335575688 ;
$ testCoords [ 275 ] = - 30 ;
// Create a truecolor image (for anti-aliasing)
$ im = imagecreatetruecolor ( GRAPH_WIDTH , GRAPH_HEIGHT ) ;
// Set Colors
$ bgColor = imagecolorallocate ( $ im , 224 , 223 , 223 ) ;
$ textColor = imagecolorallocate ( $ im , 0 , 0 , 0 ) ;
$ axisColor = imagecolorallocate ( $ im , 64 , 64 , 64 ) ;
$ dotColor = imagecolorallocate ( $ im , 192 , 64 , 64 ) ;
$ graphColor = imagecolorallocate ( $ im , 64 , 64 , 192 ) ;
//Background
imagefill ( $ im , 0 , 0 , $ bgColor ) ;
// Create a graph object
$ testGraph = new Plot ( $ testCoords ) ;
// Optional: draw known points
// By passing GRAPH_WIDTH / 2 and GRAPH_HEIGHT / 2, we shift the origin to the center of the image
$ testGraph -> drawDots ( $ im , $ dotColor , GRAPH_WIDTH / 2 , GRAPH_HEIGHT / 2 , 5 ) ;
// Create a spline object
$ curve = new CubicSpline ( ) ;
// Passing coordinates to it, rendering step = 5
$ curve -> setCoords ( $ testCoords , 5 ) ;
if ( ! $ curve -> getError ( ) )
{
// Calculate the coordinates of the curve
$ curveCoords = $ curve -> process ( ) ;
if ( $ r )
{
// Another graph object
$ curveGraph = new Plot ( $ curveCoords ) ;
// Draw the curve
$ curveGraph -> drawLine ( $ im , $ graphColor , GRAPH_WIDTH / 2 , GRAPH_HEIGHT / 2 ) ;
}
}
// Give it to the user
header ( "Content-type: image / png" ) ;
imagepng ( $ im ) ;
imagedestroy ( $ im ) ;
?>
Download library and demo version
Todo
- You can combine setCoords and process () into one method - there is no use in separating them.
- Improve error handling.
- Antialiasing sometimes does not work very well - a “ladder” is visible on vertical lines with small steps.
- Allow multiple Y values for one X for a Bezier curve.
- The Plot object must be made reusable - do not pass coordinates to the constructor, as now.
- Add comments in the code and documentation

Literature
E.P. Kuzmin, D.V. Ivanov Algorithmic Basics of Computer Graphics (Lecture No. 4)
Spline Interpolation
Original article Akims
Comparison of cubic and Akima spline
Bezier Curves Made Simple
Wikipedia:
Lagrange polynomial .
Cubic spline
Bezier curves
Source: https://habr.com/ru/post/130873/
All Articles