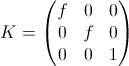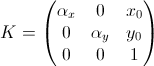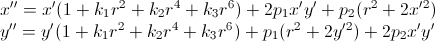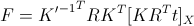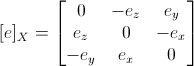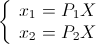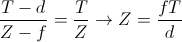Basics of stereo vision
This article contains basic information about the mathematical apparatus used in stereo vision. The idea of writing it appeared after I started working with stereo vision methods, in particular, using algorithms implemented in OpenCV . These algorithms often refer to different concepts, such as "fundamental matrix", "epipolar geometry", "triangulation". There are very good books on computer vision, which describe, including stereo vision and all the necessary concepts, but they often contain too much information for a beginner. Here, in a brief form, basic information is presented on how stereo vision works and the basic concepts connected with it:
To understand the content of the article, it is enough to have a general idea of analytical geometry and linear algebra: to know what a matrix, vector, scalar and vector product is.
')
For further exposition, one will need mainly an understanding of the analytical approach to projective geometry, and it is precisely this that is set forth below.
Points of the projective plane. Consider a two-dimensional projective space (which is also called a projective plane). While on a normal Euclidean plane, points are described by a pair of coordinates ( x , y ) T , on a projective plane, points are described by a three-component vector ( x , y , w ) T. Moreover, for any nonzero number a , the vectors ( x , y , w ) T and ( ax , ay , aw ) T correspond to the same point. And the zero vector (0,0,0) T does not correspond to any point and is thrown out of consideration. Such a description of points on a plane is called homogeneous coordinates (homogeneous coordinates).
The points of the projective plane can be associated with the points of an ordinary Euclidean plane. To the coordinate vector ( x , y , w ) T with w ≠ 0, we associate a point of the Euclidean plane with the coordinates ( x / w , y / w ) T. If w = 0, i.e. Since the coordinate vector has the form ( x , y , 0 T ), then we will say that this point is at infinity. Thus, the projective plane can be considered as a Euclidean plane, complemented by points from infinity.
You can move from homogeneous coordinates ( x , y , w ) T to ordinary Euclidean coordinates by dividing the coordinate vector by the last component and then discarding it ( x , y , w ) T → ( x / w , y / w ) T. And from the Euclidean coordinates ( x , y ) T one can move to homogeneous coordinates by adding the coordinate vector with the unit number: ( x , y ) T → ( x , y , 1) T
Lines on the projective plane. Any line on the projective plane is described, like a point, by a three-component vector l = ( a , b , c ) T. Again, the vector describing a straight line is defined up to a nonzero multiplier. In this case, the equation of the line will be: l T x = 0.
In the case when a 2 + b 2 ≠ 0 we have an analogue of the usual straight line ax + by + c = 0. And the vector (0,0, w ) corresponds to the straight line lying at infinity.
Three-dimensional projective space. By analogy with the projective plane, the points of the three-dimensional projective space are determined by the four-component vector of homogeneous coordinates ( x , y , z , w ) T. Again for any nonzero number a , the coordinate vectors ( x , y , z , w ) T and ( ax , ay , az , aw ) T correspond to the same point.
As in the case of a projective plane, a correspondence can be established between the points of a three-dimensional Euclidean space and a three-dimensional projective space. The vector of homogeneous coordinates ( x , y , z , w ) T with w 0 corresponds to a point of the Evklod space with coordinates ( x / w , y / w , z / w ) T. And about a point with a vector of homogeneous coordinates of the form ( x , y , z , 0) T say that it lies at infinity.
Projective transformation. One more thing that will be needed for further exposition is projective transformations (homography, projective transformation - in English literature). From a geometrical point of view, a projective transformation is a reversible transformation of a projective plane (or space) that takes straight lines into straight lines. In coordinates, the projective transformation is expressed as a non-degenerate square matrix H , and the coordinate vector x is transformed into the coordinate vector x 'by the following formula: x ' = H x .
The projection formula has a simple mathematical notation in homogeneous coordinates:
The matrix P is expressed as P = KR [ I | - c ] = K [ R | t ], where K is the upper triangular matrix of internal parameters of a 3 × 3 camera (a specific view is shown below), R is an orthogonal matrix of size 3 × 3 that determines the rotation of the camera relative to the global coordinate system, I is a 3 × 3 unit matrix, a vector c - coordinates of the center of the camera, and t = - R c .
It is worth noting that the matrix of the camera is determined up to a constant nonzero multiplier, which will not change the results of projecting points using the formula x = P X. However, this constant multiplier is usually chosen so that the matrix of the camera would look like this.
In the simplest case, when the center of the camera lies at the origin, the main axis of the camera is aligned with the Cz axis, the coordinate axes on the camera plane have the same scale (which is equivalent to square pixels), and the center of the image has zero coordinates, the camera matrix is equal to P = K [ I | 0 ] where
In addition, due to the non-ideality of optics, distortion-distortion is present in the images obtained from cameras. These distortions have a non-linear mathematical record:
Distortions do not depend on the distance to the object, but depend only on the coordinates of the points at which the pixels of the object are projected. Accordingly, to compensate for distortions, the source image is usually converted from a camera. This transformation will be the same for all images obtained from the camera, provided that the focal length is constant (mathematically - the same matrix of internal parameters).
In a situation when the internal parameters of the camera and the distortion coefficients are known, they say that the camera is calibrated.
Matrix pairs of cameras, calibration. Let there be two cameras defined by their matrices P and P 'in some coordinate system. In this case, they say that there are a couple of calibrated cameras. If the centers of the cameras do not coincide, then this pair of cameras can be used to determine the three-dimensional coordinates of the observed points.
Often, the coordinate system is chosen so that the matrices of the cameras have the form P = K [ I | 0], P '= K ' [ R '| t ']. This can always be done if we choose the coordinate origin coinciding with the center of the first camera and direct the Z axis along its optical axis.
Calibration of cameras is usually performed, due to repeated shooting of some calibration pattern, on the image you can easily identify key points for which their relative positions in space are known. Next, the systems of equations are compiled and solved (approximate), relating the coordinates of the projections, the matrix of chambers and the position of the pattern points in space.
There are commonly available implementations of calibration algorithms, for example, the Matlab Calibration toolbox . The OpenCV library also includes camera calibration algorithms and a calibration pattern search in an image.
Epipolar geometry. Before proceeding to the description of the actual method of calculating the three-dimensional coordinates of points, I will describe some important geometric properties relating the positions of the projections of a point in three-dimensional space on images from both cameras.
Thus, each point x in the image of the left camera corresponds to the epipolar line l 'in the image of the right camera. At the same time, the pair for x in the image of the right camera can lie only on the corresponding epipolar line. Similarly, each point x 'in the right image corresponds to an epipolar line l on the left.
Epipolar geometry is used to search for stereo pairs, and to check that a pair of points can be a stereo pair (that is, a projection of a certain point in space).
Epipolar geometry has a very simple entry in coordinates. Let there be a pair of calibrated cameras, and let x be the homogeneous coordinates of a point in the image of one camera, and x 'in the image of the second one. There exists a 3 × 3 matrix F such that a pair of points x , x 'is a stereo pair if and only if:
In the case when the camera matrices have the form P = K [ I | 0], P '= K ' [ R | t ] the fundamental matrix can be calculated by the formula:
In addition to the fundamental matrix, there is also such a thing as the essential matrix: E = K ' T F K. In the case when the matrix of internal parameters will be unity, the essential matrix will coincide with the fundamental one. The essential matrix can restore the position and rotation of the second camera relative to the first, so it is used in tasks in which you need to determine the movement of the camera.
Triangulation of points (triangulation). Now let's move on to how to determine the three-dimensional coordinates of a point by the coordinates of its projections. This process is called triangulation in the literature.
Suppose there are two calibrated cameras with matrices P 1 and P 2 . x 1 and x 2 are the homogeneous coordinates of the projections of some point of the space X. Then you can make the following system of equations:
The idea underlying the construction of the depth map of a stereo pair is very simple. For each point on one image, a pair point is searched for it on another image. And by a pair of corresponding points, you can perform triangulation and determine the coordinates of their pre-image in three-dimensional space. Knowing the three-dimensional coordinates of the pre-image, the depth is calculated as the distance to the camera plane.
The pair point must be sought on the epipolar line. Accordingly, to simplify the search, the images are aligned so that all the epipolar lines are parallel to the sides of the image (usually horizontal). Moreover, the images are aligned so that for the point with coordinates ( x 0 , y 0 ) the corresponding epipolar line is given by the equation x = x 0 , then for each point the corresponding pair point must be searched for in the same line in the image from the second cameras. This image alignment process is called rectification. Usually, the rectification is done by re-imaging the image and it is combined with getting rid of distortions. An example of the rectified images is shown in Figure 3, the pictures are taken from the database of images comparing various methods for constructing a depth map http://vision.middlebury.edu/stereo .
- projective geometry and uniform coordinates
- camera model
- epipolar geomerty, fundamental and essential matrix
- triangulation of stereo pairs of points
- depth map (disparity map) and the idea behind its calculation
To understand the content of the article, it is enough to have a general idea of analytical geometry and linear algebra: to know what a matrix, vector, scalar and vector product is.
1 Projective geometry and homogeneous coordinates
In the geometry of stereo vision, projective geometry plays a significant role. There are several approaches to projective geometry: geometrical (like Euclidean geometry to introduce the concept of geometric objects, axioms and from this to deduce all properties of projective space), analytical (to consider everything in coordinates, as in an analytical approach to Euclidean geometry), algebraic.')
For further exposition, one will need mainly an understanding of the analytical approach to projective geometry, and it is precisely this that is set forth below.
Points of the projective plane. Consider a two-dimensional projective space (which is also called a projective plane). While on a normal Euclidean plane, points are described by a pair of coordinates ( x , y ) T , on a projective plane, points are described by a three-component vector ( x , y , w ) T. Moreover, for any nonzero number a , the vectors ( x , y , w ) T and ( ax , ay , aw ) T correspond to the same point. And the zero vector (0,0,0) T does not correspond to any point and is thrown out of consideration. Such a description of points on a plane is called homogeneous coordinates (homogeneous coordinates).
The points of the projective plane can be associated with the points of an ordinary Euclidean plane. To the coordinate vector ( x , y , w ) T with w ≠ 0, we associate a point of the Euclidean plane with the coordinates ( x / w , y / w ) T. If w = 0, i.e. Since the coordinate vector has the form ( x , y , 0 T ), then we will say that this point is at infinity. Thus, the projective plane can be considered as a Euclidean plane, complemented by points from infinity.
You can move from homogeneous coordinates ( x , y , w ) T to ordinary Euclidean coordinates by dividing the coordinate vector by the last component and then discarding it ( x , y , w ) T → ( x / w , y / w ) T. And from the Euclidean coordinates ( x , y ) T one can move to homogeneous coordinates by adding the coordinate vector with the unit number: ( x , y ) T → ( x , y , 1) T
Lines on the projective plane. Any line on the projective plane is described, like a point, by a three-component vector l = ( a , b , c ) T. Again, the vector describing a straight line is defined up to a nonzero multiplier. In this case, the equation of the line will be: l T x = 0.
In the case when a 2 + b 2 ≠ 0 we have an analogue of the usual straight line ax + by + c = 0. And the vector (0,0, w ) corresponds to the straight line lying at infinity.
Three-dimensional projective space. By analogy with the projective plane, the points of the three-dimensional projective space are determined by the four-component vector of homogeneous coordinates ( x , y , z , w ) T. Again for any nonzero number a , the coordinate vectors ( x , y , z , w ) T and ( ax , ay , az , aw ) T correspond to the same point.
As in the case of a projective plane, a correspondence can be established between the points of a three-dimensional Euclidean space and a three-dimensional projective space. The vector of homogeneous coordinates ( x , y , z , w ) T with w 0 corresponds to a point of the Evklod space with coordinates ( x / w , y / w , z / w ) T. And about a point with a vector of homogeneous coordinates of the form ( x , y , z , 0) T say that it lies at infinity.
Projective transformation. One more thing that will be needed for further exposition is projective transformations (homography, projective transformation - in English literature). From a geometrical point of view, a projective transformation is a reversible transformation of a projective plane (or space) that takes straight lines into straight lines. In coordinates, the projective transformation is expressed as a non-degenerate square matrix H , and the coordinate vector x is transformed into the coordinate vector x 'by the following formula: x ' = H x .
2 Model of the projective camera
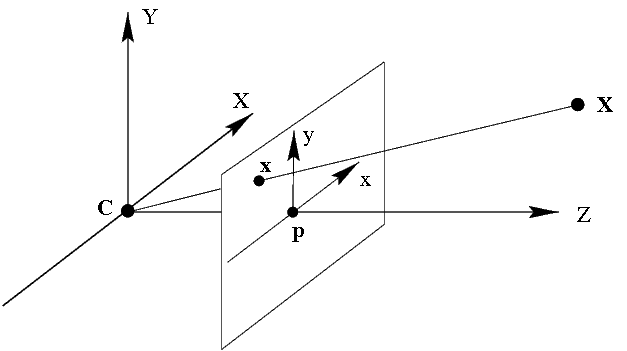
Modern CCD cameras are well described using the following model, called a projective camera (projective camera, pinhole camera). A projective camera is determined by the center of the camera , the main axis — the beam starting at the center of the camera and directed to where the camera is looking, the image plane — the plane on which the points are projected, and the coordinate system on this plane. In such a model, an arbitrary point of space X is projected onto the image plane at the point x lying on the segment CX , which connects the center of camera C with the initial point X (see Fig. 1).
Figure 1: Camera Model. C is the center of the chamber, Cp is the main axis of the chamber. The point X of the three-dimensional space is projected to the point x - on the image plane.
The projection formula has a simple mathematical notation in homogeneous coordinates:
where X is the homogeneous coordinates of a point in space, x is the homogeneous coordinates of a point of the plane, P is the matrix of a 3 × 4 camera.
x = P X
The matrix P is expressed as P = KR [ I | - c ] = K [ R | t ], where K is the upper triangular matrix of internal parameters of a 3 × 3 camera (a specific view is shown below), R is an orthogonal matrix of size 3 × 3 that determines the rotation of the camera relative to the global coordinate system, I is a 3 × 3 unit matrix, a vector c - coordinates of the center of the camera, and t = - R c .
It is worth noting that the matrix of the camera is determined up to a constant nonzero multiplier, which will not change the results of projecting points using the formula x = P X. However, this constant multiplier is usually chosen so that the matrix of the camera would look like this.
In the simplest case, when the center of the camera lies at the origin, the main axis of the camera is aligned with the Cz axis, the coordinate axes on the camera plane have the same scale (which is equivalent to square pixels), and the center of the image has zero coordinates, the camera matrix is equal to P = K [ I | 0 ] where
With real CCD cameras, pixels are usually slightly different from square, and the center of the image has non-zero coordinates. In this case, the matrix of internal parameters will take the form:
The coefficients f , α x , α y - are called the focal lengths of the camera (respectively, common and along the x and y axes).
In addition, due to the non-ideality of optics, distortion-distortion is present in the images obtained from cameras. These distortions have a non-linear mathematical record:
where k 1 , k 2 , p 1 , p 2 , k 3 are the distortion coefficients, which are parameters of the optical system; r 2 = x ' 2 + y ' 2 ; ( x ', y ') - coordinates of the projection of a point relative to the center of the image with square pixels and no distortion; ( x ″, y ″) - distorted coordinates of a point relative to the center of the image with square pixels.
Distortions do not depend on the distance to the object, but depend only on the coordinates of the points at which the pixels of the object are projected. Accordingly, to compensate for distortions, the source image is usually converted from a camera. This transformation will be the same for all images obtained from the camera, provided that the focal length is constant (mathematically - the same matrix of internal parameters).
In a situation when the internal parameters of the camera and the distortion coefficients are known, they say that the camera is calibrated.
3 pair of cameras
One can speak about the determination of the three-dimensional coordinates of the observed points when there are at least two cameras.Matrix pairs of cameras, calibration. Let there be two cameras defined by their matrices P and P 'in some coordinate system. In this case, they say that there are a couple of calibrated cameras. If the centers of the cameras do not coincide, then this pair of cameras can be used to determine the three-dimensional coordinates of the observed points.
Often, the coordinate system is chosen so that the matrices of the cameras have the form P = K [ I | 0], P '= K ' [ R '| t ']. This can always be done if we choose the coordinate origin coinciding with the center of the first camera and direct the Z axis along its optical axis.
Calibration of cameras is usually performed, due to repeated shooting of some calibration pattern, on the image you can easily identify key points for which their relative positions in space are known. Next, the systems of equations are compiled and solved (approximate), relating the coordinates of the projections, the matrix of chambers and the position of the pattern points in space.
There are commonly available implementations of calibration algorithms, for example, the Matlab Calibration toolbox . The OpenCV library also includes camera calibration algorithms and a calibration pattern search in an image.
Epipolar geometry. Before proceeding to the description of the actual method of calculating the three-dimensional coordinates of points, I will describe some important geometric properties relating the positions of the projections of a point in three-dimensional space on images from both cameras.
Suppose there are two cameras, as shown in Figure 2. C is the center of the first camera, C 'is the center of the second camera. The point of space X is projected in x onto the image plane of the left camera and into x 'onto the image plane of the right camera. The xX ray is the image of the point x in the image of the left camera. This beam is projected onto the plane of the second camera in a straight line l ', called the epipolar line. The image of point X on the image plane of the second camera necessarily lies on the epipolar line l '.
Figure 2: Epipolar Geometry
Thus, each point x in the image of the left camera corresponds to the epipolar line l 'in the image of the right camera. At the same time, the pair for x in the image of the right camera can lie only on the corresponding epipolar line. Similarly, each point x 'in the right image corresponds to an epipolar line l on the left.
Epipolar geometry is used to search for stereo pairs, and to check that a pair of points can be a stereo pair (that is, a projection of a certain point in space).
Epipolar geometry has a very simple entry in coordinates. Let there be a pair of calibrated cameras, and let x be the homogeneous coordinates of a point in the image of one camera, and x 'in the image of the second one. There exists a 3 × 3 matrix F such that a pair of points x , x 'is a stereo pair if and only if:
The matrix F is called the fundamental matrix. Its rank is 2, it is determined up to a nonzero multiplier and depends only on the matrices of the source cameras P and P '.
x ' T F x = 0
In the case when the camera matrices have the form P = K [ I | 0], P '= K ' [ R | t ] the fundamental matrix can be calculated by the formula:
where for vector e the designation [ e ] X is calculated as
With the help of the fundamental matrix, the equations of the epipolar lines are calculated. For point x , the vector defining the epipolar line will have the form l '= F x , and the equation of the epipolar line itself: l ' T x '= 0. Similarly for the point x ', the vector defining the epipolar line will look like l = F T x '.
In addition to the fundamental matrix, there is also such a thing as the essential matrix: E = K ' T F K. In the case when the matrix of internal parameters will be unity, the essential matrix will coincide with the fundamental one. The essential matrix can restore the position and rotation of the second camera relative to the first, so it is used in tasks in which you need to determine the movement of the camera.
Triangulation of points (triangulation). Now let's move on to how to determine the three-dimensional coordinates of a point by the coordinates of its projections. This process is called triangulation in the literature.
Suppose there are two calibrated cameras with matrices P 1 and P 2 . x 1 and x 2 are the homogeneous coordinates of the projections of some point of the space X. Then you can make the following system of equations:
In practice, the following approach is used to solve this system. Vector multiply the first equation by x 1 , the second by x 2 , get rid of linearly dependent equations and bring the system to the form A X = 0, where A has a size of 4 × 4. Then you can either proceed from that vector X is the homogeneous coordinates of the point, put its last component is 1 and solve the resulting system of 3 equations with three unknowns. An alternative way is to take any nonzero solution of the system A X = 0, for example, calculated as a singular vector corresponding to the smallest singular number of the matrix A.
4 Building a depth map
A depth map is an image in which, for each pixel, instead of a color, its distance from the camera is stored. A depth map can be obtained using a special depth camera (for example, the Kinect sensor is a kind of such camera), and it can also be constructed from a stereo pair of images.The idea underlying the construction of the depth map of a stereo pair is very simple. For each point on one image, a pair point is searched for it on another image. And by a pair of corresponding points, you can perform triangulation and determine the coordinates of their pre-image in three-dimensional space. Knowing the three-dimensional coordinates of the pre-image, the depth is calculated as the distance to the camera plane.
The pair point must be sought on the epipolar line. Accordingly, to simplify the search, the images are aligned so that all the epipolar lines are parallel to the sides of the image (usually horizontal). Moreover, the images are aligned so that for the point with coordinates ( x 0 , y 0 ) the corresponding epipolar line is given by the equation x = x 0 , then for each point the corresponding pair point must be searched for in the same line in the image from the second cameras. This image alignment process is called rectification. Usually, the rectification is done by re-imaging the image and it is combined with getting rid of distortions. An example of the rectified images is shown in Figure 3, the pictures are taken from the database of images comparing various methods for constructing a depth map http://vision.middlebury.edu/stereo .
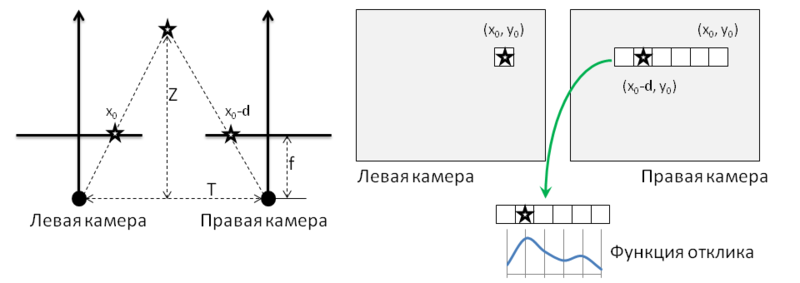
After the images are rectified, they search for the corresponding pairs of points. The easiest way is illustrated in picture 4 and consists of the following. For each pixel of the left picture with coordinates ( x 0 , y 0 ), a pixel is searched in the right picture. It is assumed that the pixel in the right picture should have coordinates ( x 0 - d , y 0 ), where d is a quantity called disparity. The search for the corresponding pixel is performed by calculating the maximum of the response function, which can be, for example, the correlation of neighborhoods of pixels. The result is a disparity map, an example of which is shown in Fig. 3
Figure 3: An example of the rectified images, and the corresponding disparity map.
The actual depth values are inversely proportional to the magnitude of the displacement of the pixels. If we use the symbols from the left half of Figure 4, then the relationship between disparity and depth can be expressed in the following way:
Figure 4: Depth Map Calculation.
Due to the inverse relationship of depth and displacement, the resolution of stereo-vision systems that work on the basis of this method is better at close distances, and worse at far distances.
Source: https://habr.com/ru/post/130300/
All Articles