Float Arithmetic Operations
All Habr's readers are somehow connected with the IT direction. Whether you are a programmer or working with hardware, networks, and so on, we all know common concepts.
Sometime in the second year of university, I became acquainted with one of the things that, in my opinion, each of us should know, well, or at least hear about her in such an article. This is the standard for representing floating point numbers (in other floating point sources). How did I get this name: IEEE-754 standard.
I am sure that each of the IT specialists at least once heard with floating point numbers, but for the first time it seemed to me utter nonsense. And it’s not simple: after all, the subject on which we studied the standard was called “Computer Architecture” and the teacher was, and now there is a living legend. Well, this is offtop.
')
So what is this IEEE-754 standard? I will say right away that at the university we were given it electronically in Russian, but I could not find it on the Internet, even when I reached Google’s 30th page. There was an example in English in which the author wrote it at 4:36 AM. I even found a website that says that if Satan decided to take over the Earth slowly, he would have created this standard. But it was created by people just like you and me.
The standard itself is a description of binary floating-point arithmetic operations. It also describes the exceptional situations that arise in such cases, writing to such a format, and much more. Naturally, after reading it, and even with such difficulty, I did not understand anything! After all, I did not know anything about the format with a floating point. But this is rude, saying the fractional part of any number, only the accuracy must be known.
On this subject, at the university, we calculated RGR (Settlement-Graphic Work), and for some reason, then I realized that if I spent more time with it than anything, I was right. This was probably the turning point of my studies. I sat at night over this standard and over the task specifically set before me: "Dividing two numbers in floating-point double precision format with replacing chains of continuous units with zeros and rounding to the nearest even one." Then it was impossible to understand. And the IEEE-754 standard always followed alongside this assignment. In fact, there was everything, absolutely everything that I needed.
Well, now in more detail about the IEEE-754 standard. It consists of several chapters that I would like to describe in more detail.
Everything starts as always with an introduction. The fact that there are programs is much more complicated than what I saw. It tells about the history of the creation of the standard. After all, programs are becoming more and more difficult, and digital computers are aging and should be replaced with a new architecture. This led to the fact that IEEE (Institute of Electrical and Electronics Engineers of the United States) at the end of the 70s created a commission that considered many proposals. The result of the commission’s work was the IEEE 754 standard “Binary floating point arithmetic” (1985), which became international. Its foundations were developed by William Kahan, a professor of mathematics at the University of Berkeley.
In the following years, standards were developed based on IEEE 754 - 1985:
- IEEE 854 - 1987, covering decimal arithmetic as well as binary;
- IEC 60559 - 1989 IEC ≪ Binary floating point arithmetic for
microprocessor systems (IEC - International Electrotechnical Commission).
The IEEE 754 standard does not obligate, but recommends the use of a package of formats specified in it, methods of data coding, rounding of results, and much more. The task of choosing the format for the designer of a universal digital computer was extremely simplified, and from that time the company began to produce universal digital computers with floating point arithmetic that satisfy the standard recommendations. The task of programmers is also somewhat simplified, since There is no need to study the features of binary floating-point arithmetic of different digital computers, it is enough to master the knowledge of the standard.
But we must remember that standards are conservative, but not eternal. And, nevertheless, this standard we all use with you, colleagues.
The standard supports several formats: single precision (32 bits), double (64 bits) and double enhanced precision. Other formats are also provided to prevent rounding errors, etc. The standard describes cases of exceptional situations: Nan, infinity, division by zero, etc. Nothing like? A very important role is played by rounding numbers in floating point format. This is also described in the standard.
And finally, the main section - Performing floating-point operations on numbers. This section describes all the arithmetic operations from comparison to division, as well as all the nuances when performing such operations. About this section can not be said like this, "in a nutshell." Let me just say that this is a real confusion, and I was faced with the task of understanding how this happens.
I will briefly describe my algorithm for the work "Floating-point division". After we received the operands A and B, we had to check them for all possible cases of exceptional situations. This is the division by zero and Nan and infinity. A little below, the table shows the types of numbers that the format supports:
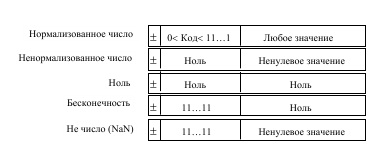
If the operands were actually numbers in the IEEE-754 format, the second stage of the operation began: the reduction of orders. It's no secret that floating-point numbers look like this:

This is a single precision representation of a number.
The order of a number in a digital computer is, in my understanding, the ordinal number of a number in a digital computer, that is, its order. Surely there is a scientific definition, but it only confuses even more. So, since the numbers have different orders, they can not be divided. You must first reduce the orders to the same type by the offset of the orders. But for this purpose it was required to analyze the orders for min and max value. And when the order shift occurs, the mantissas also shift. If the orders are equal, you need to check the mantissas, whether they have flown out of the borders and whether they are not filled with zeros, etc. After completing a series of checks, you can proceed to the most important thing: finally divide the mantissas. Well, everything is simple, like all binary arithmetic. I divided the divisor by the dividend, and wrote down the remainder in the register and added it. There are still several ways to divide: with the restoration and without the restoration of the residue. And that's not all! In the end, it was necessary to round the result according to the desired condition and determine the sign of the quotient.
It's just in words, even though it sounds scary, in fact it looks much better. Then I openly ignored this standard, which brought me not only deeper knowledge in digital computers and binary arithmetic, but also the pleasure that I could do it, the pleasure of knowing that I know something very important.
I have everything, in fact, the topic is very interesting and fascinating. Who is interested, I will gladly throw off the IEEE-754 standard and answer your questions.
Thank.
Sometime in the second year of university, I became acquainted with one of the things that, in my opinion, each of us should know, well, or at least hear about her in such an article. This is the standard for representing floating point numbers (in other floating point sources). How did I get this name: IEEE-754 standard.
I am sure that each of the IT specialists at least once heard with floating point numbers, but for the first time it seemed to me utter nonsense. And it’s not simple: after all, the subject on which we studied the standard was called “Computer Architecture” and the teacher was, and now there is a living legend. Well, this is offtop.
')
So what is this IEEE-754 standard? I will say right away that at the university we were given it electronically in Russian, but I could not find it on the Internet, even when I reached Google’s 30th page. There was an example in English in which the author wrote it at 4:36 AM. I even found a website that says that if Satan decided to take over the Earth slowly, he would have created this standard. But it was created by people just like you and me.
The standard itself is a description of binary floating-point arithmetic operations. It also describes the exceptional situations that arise in such cases, writing to such a format, and much more. Naturally, after reading it, and even with such difficulty, I did not understand anything! After all, I did not know anything about the format with a floating point. But this is rude, saying the fractional part of any number, only the accuracy must be known.
On this subject, at the university, we calculated RGR (Settlement-Graphic Work), and for some reason, then I realized that if I spent more time with it than anything, I was right. This was probably the turning point of my studies. I sat at night over this standard and over the task specifically set before me: "Dividing two numbers in floating-point double precision format with replacing chains of continuous units with zeros and rounding to the nearest even one." Then it was impossible to understand. And the IEEE-754 standard always followed alongside this assignment. In fact, there was everything, absolutely everything that I needed.
Well, now in more detail about the IEEE-754 standard. It consists of several chapters that I would like to describe in more detail.
Everything starts as always with an introduction. The fact that there are programs is much more complicated than what I saw. It tells about the history of the creation of the standard. After all, programs are becoming more and more difficult, and digital computers are aging and should be replaced with a new architecture. This led to the fact that IEEE (Institute of Electrical and Electronics Engineers of the United States) at the end of the 70s created a commission that considered many proposals. The result of the commission’s work was the IEEE 754 standard “Binary floating point arithmetic” (1985), which became international. Its foundations were developed by William Kahan, a professor of mathematics at the University of Berkeley.
In the following years, standards were developed based on IEEE 754 - 1985:
- IEEE 854 - 1987, covering decimal arithmetic as well as binary;
- IEC 60559 - 1989 IEC ≪ Binary floating point arithmetic for
microprocessor systems (IEC - International Electrotechnical Commission).
The IEEE 754 standard does not obligate, but recommends the use of a package of formats specified in it, methods of data coding, rounding of results, and much more. The task of choosing the format for the designer of a universal digital computer was extremely simplified, and from that time the company began to produce universal digital computers with floating point arithmetic that satisfy the standard recommendations. The task of programmers is also somewhat simplified, since There is no need to study the features of binary floating-point arithmetic of different digital computers, it is enough to master the knowledge of the standard.
But we must remember that standards are conservative, but not eternal. And, nevertheless, this standard we all use with you, colleagues.
The standard supports several formats: single precision (32 bits), double (64 bits) and double enhanced precision. Other formats are also provided to prevent rounding errors, etc. The standard describes cases of exceptional situations: Nan, infinity, division by zero, etc. Nothing like? A very important role is played by rounding numbers in floating point format. This is also described in the standard.
And finally, the main section - Performing floating-point operations on numbers. This section describes all the arithmetic operations from comparison to division, as well as all the nuances when performing such operations. About this section can not be said like this, "in a nutshell." Let me just say that this is a real confusion, and I was faced with the task of understanding how this happens.
I will briefly describe my algorithm for the work "Floating-point division". After we received the operands A and B, we had to check them for all possible cases of exceptional situations. This is the division by zero and Nan and infinity. A little below, the table shows the types of numbers that the format supports:

If the operands were actually numbers in the IEEE-754 format, the second stage of the operation began: the reduction of orders. It's no secret that floating-point numbers look like this:

This is a single precision representation of a number.
The order of a number in a digital computer is, in my understanding, the ordinal number of a number in a digital computer, that is, its order. Surely there is a scientific definition, but it only confuses even more. So, since the numbers have different orders, they can not be divided. You must first reduce the orders to the same type by the offset of the orders. But for this purpose it was required to analyze the orders for min and max value. And when the order shift occurs, the mantissas also shift. If the orders are equal, you need to check the mantissas, whether they have flown out of the borders and whether they are not filled with zeros, etc. After completing a series of checks, you can proceed to the most important thing: finally divide the mantissas. Well, everything is simple, like all binary arithmetic. I divided the divisor by the dividend, and wrote down the remainder in the register and added it. There are still several ways to divide: with the restoration and without the restoration of the residue. And that's not all! In the end, it was necessary to round the result according to the desired condition and determine the sign of the quotient.
It's just in words, even though it sounds scary, in fact it looks much better. Then I openly ignored this standard, which brought me not only deeper knowledge in digital computers and binary arithmetic, but also the pleasure that I could do it, the pleasure of knowing that I know something very important.
I have everything, in fact, the topic is very interesting and fascinating. Who is interested, I will gladly throw off the IEEE-754 standard and answer your questions.
Thank.
Source: https://habr.com/ru/post/130272/
All Articles