Clipping algorithms
With the growth of computer power, more and more people are trying to work with graphics. At first glance, many algorithms seem intuitive, but if you want your application to work at an acceptable speed, you will have to learn classical algorithms.
This post is devoted to the analysis of several algorithms aimed at the same task, the task of cutting off segments. When generating images, figures of arbitrary shape and size can be obtained. Often, monitors cannot display the generated images entirely. Also sometimes there are situations when it is necessary to set the image area on the screen and display images only inside this area. To solve these problems, cut-off algorithms were invented.
The simplest clipping problem is the line clipping problem. We formulate it on a specific example. We assume that the output region is given by the rectangle ABCD. Consider an example, and take the triangle PRQ as a cut figure.
')
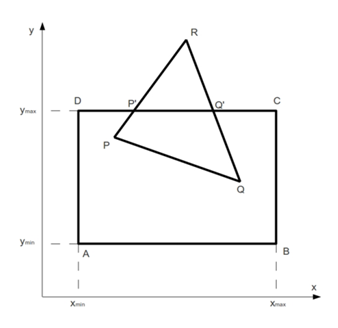
The clipping process should be performed fully automatically. Those. for the drawing of the triangle PRQ, only the commands for drawing the segments PQ; PP '; Q' Q must be executed. At the same time, the coordinates of the points P '; Q' are not known in advance.
In practice, a large number of mutual locations of the points of the segment and the output area are possible. This variety makes the clipping operation very non-trivial from an algorithmic point of view. To solve these problems, cut-off algorithms have been created.
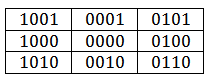
Quite interesting is the clipping algorithm proposed by Sutherland and Cohen. The essence of the algorithm is that a four-bit code is assigned to the ends of a segment: b 0 , b 1 , b 2 , b 3 . This four-bit code contains information about the position of a point relative to the output area. In practice, there are 9 combinations:
We explain these codes:
We explain these codes:
After the codes are received, the following options are possible:
The first two cases are easily verified using bitwise logical operations. Of greatest interest is the third case. Consider it on a small specific example.

If the code of any of the ends contains a single bit, then either P 1 or P 2 moves from outside the window to one of its borders (or to its continuation). Those. point P 1 moves to point R, and P 2 moves to point U. For new points, we again calculate four-bit codes. In our case, the ends of the segment still lie outside the window, i.e. we need one more movement: point R move to point S, and point U move to point T. It turns out that the clipping process is iterative. Since at each step the distance between the ends of the segment decreases, we can say that the algorithm will converge. As a result, a segment will be obtained (in our case (S; T), which should be displayed).
Consider the work of this algorithm on another example.

The location of the segment (P 1 ; P 2 ) does not meet either the conditions of full visibility or the conditions of complete invisibility, so in this case, too, resort to the operation of transfer of points.

After the carried out transfers, the codes of the ends of the segment satisfy the second condition, i.e. the entire segment will not be displayed on the screen.
In the Sutherland-Cohen algorithm, the search for the point of intersection of the segment with the window border can take several iterations. This can be avoided if you implement a search for an intersection point using a binary search. This idea was proposed by Sprull and Sutherland. The software implementation of this algorithm is slower than the Sutherland-Cohen algorithm, but the hardware implementation is faster, since the basic operations of the algorithm are very efficiently implemented in hardware.

This method also uses the four-bit code described above. With the help of these codes, cases of trivial visibility (a) and trivial invisibility (b) are easily identified. The remaining (non-trivial) segments are divided into two equal parts, and checks are performed for two newly obtained segments. Division and checks will be performed until an intersection with the side of the window is detected, or until the segment degenerates into a point. After the segment has degenerated, we determine its visibility and, depending on the result, either draw the current or not.
Consider the segment c. Obviously, this segment lies entirely outside the window, but it cannot be rejected immediately. That is why we perform half divisions and exclude some parts of the segment. The division ends at the moment when the segment turns into a point. Making sure that the resulting point is invisible, we conclude that the entire segment should not be drawn.
The segment d is also not defined trivially. Its division into two halves (point 3) leads to the same results for both halves. The segment (3; 2) is split in half by a point 4. Theoretically, you can draw a segment (3; 4), but this is not very effective. It is more correct to remember point 4 as the visible point furthest from point 1, and continue the segment (4; 2) to break up to the intersection with the lower border of the window. The resulting point and will be considered the most distant from point 1 visible point. Similarly, the interval 3; 1 is processed, and the visible point is the farthest from point 2. Then, between these two points, the drawing takes place.
For d-type segments, it is necessary to perform two binary searches for visible points furthest from the ends of the segment. For segments of type e, the need for one of the binary searches is eliminated.
In the work of the Cyrus-Beck algorithm, a parametric representation of the segment is used: P s (t) = P 1 + (P 2 -P 1 ) * t; t∈ [0; 1]. This algorithm allows clipping not only with a rectangular window, but also with any convex polygon.
Consider a separate edge E i of the cutting polygon. Orient the normal to this edge to the outer side of the cutting polygon. We also assume that the cutting polygon is counterclockwise. Then, if the edge is the vector P (E (i 1 ) ) P E i 2 , then the normal N E i will be proportional to (y E i 2 - y E i 1 ; x E i 1 - x E i 2 ).
Denote the line on which the edge lies by L i . Then the area cut off by the line L i corresponds to points P for which the scalar product of the vectors (PP E i ) ) and N E i is greater than 0 (P E i is any point on the edge of E i ). The point of intersection of the line on which the segment lies with the cutting line L i is found from the equation ((P s (t) -P E i , N E i = 0). Solving this equation, we find t.
For the described algorithm, it is also important in what direction (inside or out of the window) a point passes when moving along the segment from P 1 to P 2 . This is determined by the sign ((P 2 -P 1 ), N E i . We will denote such intersection points as:

After calculating the coordinates of t for all possible intersections with straight lines L i , you should choose the maximum coordinate of the potentially incoming and the minimum of the potentially outgoing (t BxMax ; t Outmin ). If the line, on which the segment P 1 P 2 lies, intersects the cutting polygon, then t BxMax <t Outmin . In this case, if the intersection [t 1 , t 2 ] = [t BMax , t OutMin ] ∩ [0,1] is non-empty, then P s (t 1 ) P s (t 2 ) will be the required cut segment, otherwise In this case, the segment is completely outside the clipping region.
On these algorithms, the topic of clipping, of course, does not end there. A separate question is polygon clipping algorithms. If the topic is interesting to the community, I will definitely reveal this topic.
This post is devoted to the analysis of several algorithms aimed at the same task, the task of cutting off segments. When generating images, figures of arbitrary shape and size can be obtained. Often, monitors cannot display the generated images entirely. Also sometimes there are situations when it is necessary to set the image area on the screen and display images only inside this area. To solve these problems, cut-off algorithms were invented.
Segment cut
The simplest clipping problem is the line clipping problem. We formulate it on a specific example. We assume that the output region is given by the rectangle ABCD. Consider an example, and take the triangle PRQ as a cut figure.
')

The clipping process should be performed fully automatically. Those. for the drawing of the triangle PRQ, only the commands for drawing the segments PQ; PP '; Q' Q must be executed. At the same time, the coordinates of the points P '; Q' are not known in advance.
In practice, a large number of mutual locations of the points of the segment and the output area are possible. This variety makes the clipping operation very non-trivial from an algorithmic point of view. To solve these problems, cut-off algorithms have been created.
Sutherland-Cohen Algorithm
Quite interesting is the clipping algorithm proposed by Sutherland and Cohen. The essence of the algorithm is that a four-bit code is assigned to the ends of a segment: b 0 , b 1 , b 2 , b 3 . This four-bit code contains information about the position of a point relative to the output area. In practice, there are 9 combinations:

We explain these codes:
We explain these codes:
- b 0 = 0, if x≥x min ;
- b 0 = 1 if x <x min ;
- b 1 = 0, if x≤x max ;
- b 1 = 1, if x> x max ;
- b 2 = 0, if y≥y min ;
- b 2 = 1, if y <y min ;
- b 3 = 0, if y≤y max ;
- b 3 = 1, if y> y max ;
After the codes are received, the following options are possible:
- Codes contain only 0, which means the segment is entirely inside the window and must be drawn entirely;
- Codes contain a single bit in the same position, which means that the segment lies outside the window and will not be drawn;
- In all other cases, the window is only part of the segment, and this means that there is a need for clipping.
The first two cases are easily verified using bitwise logical operations. Of greatest interest is the third case. Consider it on a small specific example.

If the code of any of the ends contains a single bit, then either P 1 or P 2 moves from outside the window to one of its borders (or to its continuation). Those. point P 1 moves to point R, and P 2 moves to point U. For new points, we again calculate four-bit codes. In our case, the ends of the segment still lie outside the window, i.e. we need one more movement: point R move to point S, and point U move to point T. It turns out that the clipping process is iterative. Since at each step the distance between the ends of the segment decreases, we can say that the algorithm will converge. As a result, a segment will be obtained (in our case (S; T), which should be displayed).
Consider the work of this algorithm on another example.

The location of the segment (P 1 ; P 2 ) does not meet either the conditions of full visibility or the conditions of complete invisibility, so in this case, too, resort to the operation of transfer of points.

After the carried out transfers, the codes of the ends of the segment satisfy the second condition, i.e. the entire segment will not be displayed on the screen.
Midpoint algorithm
In the Sutherland-Cohen algorithm, the search for the point of intersection of the segment with the window border can take several iterations. This can be avoided if you implement a search for an intersection point using a binary search. This idea was proposed by Sprull and Sutherland. The software implementation of this algorithm is slower than the Sutherland-Cohen algorithm, but the hardware implementation is faster, since the basic operations of the algorithm are very efficiently implemented in hardware.

This method also uses the four-bit code described above. With the help of these codes, cases of trivial visibility (a) and trivial invisibility (b) are easily identified. The remaining (non-trivial) segments are divided into two equal parts, and checks are performed for two newly obtained segments. Division and checks will be performed until an intersection with the side of the window is detected, or until the segment degenerates into a point. After the segment has degenerated, we determine its visibility and, depending on the result, either draw the current or not.
Consider the segment c. Obviously, this segment lies entirely outside the window, but it cannot be rejected immediately. That is why we perform half divisions and exclude some parts of the segment. The division ends at the moment when the segment turns into a point. Making sure that the resulting point is invisible, we conclude that the entire segment should not be drawn.
The segment d is also not defined trivially. Its division into two halves (point 3) leads to the same results for both halves. The segment (3; 2) is split in half by a point 4. Theoretically, you can draw a segment (3; 4), but this is not very effective. It is more correct to remember point 4 as the visible point furthest from point 1, and continue the segment (4; 2) to break up to the intersection with the lower border of the window. The resulting point and will be considered the most distant from point 1 visible point. Similarly, the interval 3; 1 is processed, and the visible point is the farthest from point 2. Then, between these two points, the drawing takes place.
For d-type segments, it is necessary to perform two binary searches for visible points furthest from the ends of the segment. For segments of type e, the need for one of the binary searches is eliminated.
Algorithm of Cyrus Beck
In the work of the Cyrus-Beck algorithm, a parametric representation of the segment is used: P s (t) = P 1 + (P 2 -P 1 ) * t; t∈ [0; 1]. This algorithm allows clipping not only with a rectangular window, but also with any convex polygon.
Consider a separate edge E i of the cutting polygon. Orient the normal to this edge to the outer side of the cutting polygon. We also assume that the cutting polygon is counterclockwise. Then, if the edge is the vector P (E (i 1 ) ) P E i 2 , then the normal N E i will be proportional to (y E i 2 - y E i 1 ; x E i 1 - x E i 2 ).
Denote the line on which the edge lies by L i . Then the area cut off by the line L i corresponds to points P for which the scalar product of the vectors (PP E i ) ) and N E i is greater than 0 (P E i is any point on the edge of E i ). The point of intersection of the line on which the segment lies with the cutting line L i is found from the equation ((P s (t) -P E i , N E i = 0). Solving this equation, we find t.
For the described algorithm, it is also important in what direction (inside or out of the window) a point passes when moving along the segment from P 1 to P 2 . This is determined by the sign ((P 2 -P 1 ), N E i . We will denote such intersection points as:

After calculating the coordinates of t for all possible intersections with straight lines L i , you should choose the maximum coordinate of the potentially incoming and the minimum of the potentially outgoing (t BxMax ; t Outmin ). If the line, on which the segment P 1 P 2 lies, intersects the cutting polygon, then t BxMax <t Outmin . In this case, if the intersection [t 1 , t 2 ] = [t BMax , t OutMin ] ∩ [0,1] is non-empty, then P s (t 1 ) P s (t 2 ) will be the required cut segment, otherwise In this case, the segment is completely outside the clipping region.
On these algorithms, the topic of clipping, of course, does not end there. A separate question is polygon clipping algorithms. If the topic is interesting to the community, I will definitely reveal this topic.
Source: https://habr.com/ru/post/129701/
All Articles