The problem of "maximum-subarray" on the example of the dollar

What is the essence

The article proposes to find a period of dates for which it was possible to earn the most on the difference in the dollar / ruble exchange rate over the past 5 years.

In Russian, the name of the problem will sound approximately as the maximum sum of the elements of the subarray in the array . The article presents the calculation algorithm, as well as the result of his work.

How did I come to this

Recently I started to read the excellent CLRS book ( Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein. Introduction to Algorithms, Third Edition. ). As it is not difficult to guess, the book outlines the fundamental knowledge of computer science.
One of the sections of the book just leads the implementation of the algorithm to solve this problem. To consolidate the knowledge and meet my own interest, I decided to apply it on the data on the dollar / ruble rate over the past 5 years.

The essence of the problem

As can be seen from the graph over the past 5 years, the dollar has changed very much. And it would be reasonable to assume that for sure the best deal would be to buy at an absolute minimum and sell at a subsequent local maximum (which sometimes is not so easy to detect "by eye").


')
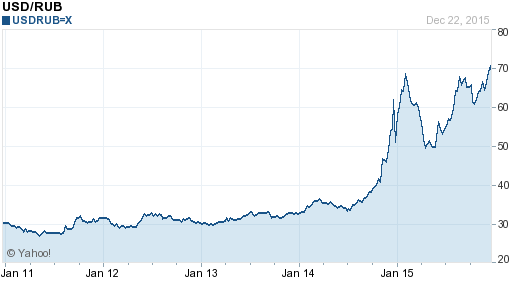
Let's check this statement.

Decision

The easiest solution would be to “go to the forehead” and search through the sums of all combinations of sub-arrays and compare them to find the maximum, but this solution takes O (n ^ 2) time not very convenient for us, since there is confidence that this can be done optimally.

By the solution we will recursively split the input array into 2 subarrays through the middle and look for the maximum amount in each and parts, as well as at their intersection. This process will require us O (n lg n), which is quite effective.

Let's paint an example:

We will receive data from www.oanda.com/currency/historical-rates in a .csv file in the format
"2011-10-02","32.1914",,,,
"2011-10-01","32.0809",,,,
"2011-09-30","31.9086",,,,
"2011-09-29","31.7294",,,,
"2011-09-28","32.0421",,,,
"2011-09-27","32.2233",,,,
"2011-09-26","32.0980",,,,
"2011-09-25","32.0673",,,,
...


Next, we need to read the data and prepare it for processing:

  courses = [] reader = csv.reader(open('data.csv', 'rb'), delimiter=',', quotechar='"') prev = 0 for row in reader: #   cur = float(row[1]) #         if prev == 0: prev = cur #    value = [row[0], prev - cur, row[1]] prev = cur courses.insert(0, value) 

The data in the file in reverse order with respect to time, so we insert them inversely. During data processing, we look for the difference in the daily rate of previous - current. Our task is just to find the maximum amount of these differences.

 def find_max_subarray(a, low, high): #   if high == low: return low, high, a[low][1] else: #   2  mid = (low + high) / 2 #     left_low, left_high, left_sum = find_max_subarray(a, low, mid) #     right_low, right_high, right_sum = find_max_subarray(a, mid + 1, high) # - cross_low, cross_high, cross_sum = find_crossing(a, low, mid, high) if (left_sum >= right_sum) & (left_sum >= cross_sum): return left_low, left_high, left_sum elif (right_sum >= left_sum) & (right_sum >= cross_sum): return right_low, right_high, right_sum else: return cross_low, cross_high, cross_sum 

And the search function of the cross-maximum (passing through the mid - mid division).

 def find_crossing(a, low, mid, high): max_left = 0 max_right = 0 left_sum = -1e308 sum = 0 #    for i in range(mid, low, -1): sum = sum + a[i][1] if sum > left_sum: left_sum = sum max_left = i max_right = 0 right_sum = -1e308 sum = 0 #    for j in range(mid + 1, high): sum = sum + a[j][1] if sum > right_sum: right_sum = sum max_right = j return max_left, max_right, left_sum + right_sum 

Well, we derive the result that interests us

 min, max, sum = find_max_subarray(courses, 0, len(courses)-1) print courses[min] print courses[max] print sum 

As a result, I received

['2008-07-16', 0.07420000000000115, '23.1269']
['2009-02-05', 0.12059999999999604, '36.1257']
13.1194


And a little play, moving the lower date for 2011

['2011-05-05', 0.006199999999999761, '27.2657']
['2011-09-26', 0.12530000000000285, '32.0980']
4.9576


All code can be found at gist.github.com/1257729

Thanks for attention!