Russian Code Cup: Final Round Results
On September 18, the final round of the Russian Code Cup All-Russian Programming Cup was held . This year 50 programmers reached the final of the Olympiad - 27 from Russia, 11 from Ukraine, 7 from Belarus, two from the USA and one each from Armenia, Georgia and Switzerland.

The winner was Peter Mitrichev from Moscow. He received a prize of 10 thousand dollars. USA. The second place was taken by Evgeny Kapun from St. Petersburg, he received $ 5,000. In third place is Mikhail Dvorkin from St. Petersburg with a prize of $ 3,000. Congratulations to the guys and wish them continued success!
')
In this article we will analyze the tasks from the final round.
A complete description of the tasks can be found here .
Problem A. Clock Translation
In this task, the rules for converting hours in several cities were set and it was required to find out the total inconvenience of residents of all cities, where the inconvenience for a couple of cities was determined as the time difference in these cities and these values were required to be summed over all hours in a year.
First, we note that one of the specified cities was the capital, and in the capital, time is not translated. Therefore, it is convenient to choose the Moscow time as the “absolute scale” of reference and use it to indicate the time of all events. First of all, let's go through all the clock translations specified in the input file and for each clock translation we define its time in the absolute scale. Now, each clock translation is characterized by three numbers:
• time on an absolute scale when it occurs,
• the city where the transfer takes place,
• the amount of translation hours.
Now we will consider the events in the order in which they occur on an absolute scale. All the time from the previous to the current event, the inconvenience in the country was constant.
Let's see how much the inconvenience has changed in the country as a result of a change in time in a certain city. Let the city have a shift of i hours relative to the capital. Let the total shift of cities that have a smaller time shift be S, and their number be L. Then the additive to the inconvenience with these cities for the current one isLi-S. Similarly, you can calculate the addition to the inconvenience with respect to cities with a greater time shift. This value should be subtracted from the total inconvenience, find out the new time shift for the city and add the corresponding value to the total inconvenience.
For a quick calculation of the total time shift in cities on a certain segment of shifts, as well as to count the number of cities in a segment, you can use, for example, a segment tree or a Fenwick tree.
Problem B. Reverse bug problem
In this task, it was required for a given number k to build a maze in which the number of paths from the left upper to the lower right cell, provided that it was allowed to move only to the right and down, would be equal to k.
Note the following. Suppose we have two mazes in which the number of ways to get from the top left to the right bottom cell is a and b, respectively.
Then, placing them in parallel, as shown in the figure, we can get a maze in which a + b ways to get from the top left to the bottom right cell, and by placing them sequentially, we get a maze in which there are ab paths.
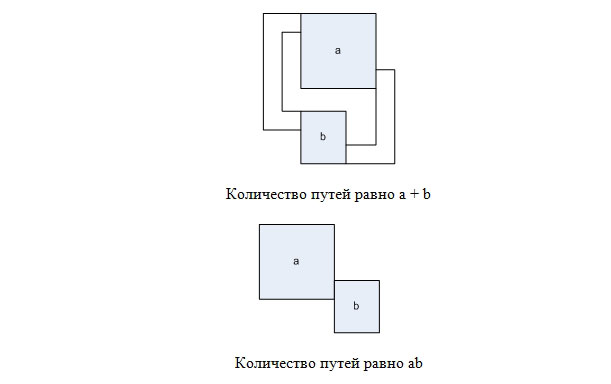
Note that in an empty maze of size 2 × 2 there are two ways, and in a maze of size 1 × 1 - one way. Therefore, by expanding the number k into a binary number system and using the described method, one can get a maze with k paths from the upper left to the right lower cell.
An example of such a maze for k = 19 is shown in the figure.
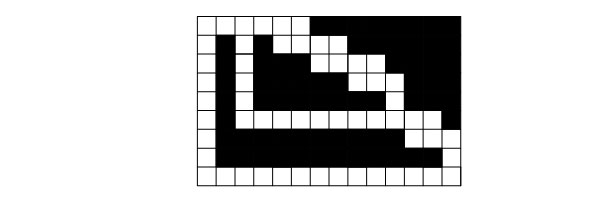
Note that for each digit of the number k, 5 cells are required horizontally, and 2 60 > 10 18 , therefore, the above scheme allows you to create a maze no larger than 300 × 300 in size, as required by the condition of the problem.
Task C. Splitting a table
In this task, it was necessary to count the number of partitions of the table of zeros and units into 9 parts, so that the number of units in the given five of these parts was even.

Perhaps several approaches to solving this problem, consider one of them. Fix c1, c2, r1 and r2. Note that with an increase in r2 by one, the parity of the number of units in parts A5, A7 and A9 does not change if the line r2 contained an even number of ones and changes otherwise. Therefore, with fixed c1, c2 and r1, it is easy to understand which r2 are suitable - depending on the parity of the number of units in the desired parts when r2 = n - 1 are suitable or such r2 that the number of units in the lines starting from r2 + 1 to n is even, is odd. We get the solution in O (n 3 ), which is still not enough to meet the allotted time limit. However, now a similar reasoning can be applied to c1 and c2. With fixed r1, r2, and c1, an increase in c2 by one changes the parity by exactly the parity of the number of units in column c2. Therefore, fixing r1, putting r2 = n - 1 and fixing c1, it is easy to find the number of values of c2 for which r2 is suitable for an even sum in large lines or for an odd sum.
The asymptotics of this solution is already O (n 2 ), which is sufficient under the given constraints.
Task D. Archiver
There are at least two different approaches to this problem: dynamic programming or a greedy algorithm.
Imagine the process of archiving a sequence in the form of a tree: each character of each of the intermediate sequences will be a vertex of the tree, the children of the vertex will be two characters that are “glued together” in the archiving process to the specified one. The original numbers are written in the leaves, and the task is to record the numbers in all intermediate vertices, and the archiving penalty is equal to the number of vertices that have different numbers in the children.
The solution using dynamic programming is arranged as follows: at each vertex u we will store the minimum total penalty p [u] [x] for the subtree if we write the number x at this vertex. Note that at the vertex it is sensible to write only the number that occurs in one of the leaves in the subtree, therefore the total number of options that should be considered is O (n log n).
Recalculation is carried out as follows: consider the vertex u with children v and w. Suppose we plan to write the value of x. If both values of p [v] [x] and p [w] [x] are defined, then one of the options to put x in u is to put x in both children, the price of this option is p [v] [x] + p [w ] [x]. There is also an option to put x only in one child. Suppose we plan to put x in v, then the cost of this variant is p [v] [x] + minp [w] + 1, where minp [w] is the minimum value of p [w] [y] over all y.
An alternative solution to using DP is a greedy solution: for each vertex we will store a list of all possible values, putting one of which to the top we will get the minimum penalty in the subtree. It turns out that in order to find the optimal set for a vertex, it suffices to try to put only optimal values in its children. Moreover, if the lists of optimal values for children overlap, then you need to take one of these numbers. If they do not intersect, then any of the meanings of each of the children will do.
The proof of the correctness of the above algorithm is left as an exercise.
Problem E. Blackjon
In this task, it is necessary to choose a subset of fractions (cards) so that their sum is equal to one. Thus, this task is a special case of the backpack problem. One possible approach to solving the problem is to bring all the fractions to a common denominator. However, the lowest common multiple (NOC) of all possible denominators is 232,792,560, which is too large a number to further solve the resulting “classical” backpack problem.
To solve the problem, it is necessary to divide it into independent subtasks. To do this, it is necessary to divide fractions into five groups depending on the denominator: fractions with denominators of 11, 13, 17, 19, as well as all other fractions. Note that if the fractions selected from any of these groups do not total an integer, then they cannot be added to fractions from other groups to an integer. This fact is due to the fact that in separate groups there are large simple denominators such that there can be no other denominators that are multiple to them except themselves.
In each group, the sum of the selected fractions must be an integer, even possibly zero. Solving the problem of a backpack for each of the groups, we find out whether it is possible to choose fractions in a group so that we can get a certain integer number. Only integers from −100 to 100 are of interest, since the sum of not more than 100 fractions, each of which does not exceed one in absolute value, does not exceed 100 in absolute value. Also note that the NOC of all possible denominators of the latter group is only 5040, there is a number of possible options for the numerator in the amount does not exceed 1 008 001. This fact allows to solve the problem of a backpack in each group in the allotted time.
Knowing which integers can be obtained in each of the groups, it is necessary to check whether by choosing one whole number in each of the groups to get an amount equal to one. This problem can be solved using the dynamic programming method. Let us introduce the value a i , j - is it possible, using the first i groups of fractions, to get the sum exactly j. The base will be the value of a 0 , 0 = true and a 0 , j = false for j from −100 to 100 except zero. The transition is as follows: a i , j = true, if at least for one k is true (a i-1 , jk and b i, k ), and false otherwise, where b i, k is a value that indicates whether group i choose fractions with sum k. The answer to the problem will be the value of a 5,1 .
To find the set of fractions that must be taken, it suffices to use the found values of the dynamics, and for each of the groups to use the standard answer recovery method for the backpack problem.
Problem F. Cutting the cake
Let's call a straight line a good one if the cut along it divides the cake into two pieces, such that there is not a single cherry on one of them and there is at least one rosette. In addition, we call interesting the angle that a straight line forms with the axis Ox. It is required to find the minimum interesting angle of a good straight line.
Consider a good line with a minimal interesting angle. Such a straight line exists, since according to the condition of the problem, when passing a straight line through roses and cherries, one can choose which piece they belong to. Otherwise, a straight line, which is an extremum point, could not exist. The following is true: either this straight line is horizontal, or it passes through a cherry and a rose. Indeed, if a good straight line is not horizontal and does not pass through a cherry or a rose, then it can be slightly rotated in the direction of decreasing the interesting angle so that it remains good. The latter contradicts the minimality condition for an interesting angle.
Check if there is a good horizontal straight is simple enough. To do this, check the horizontal lines passing through the cherries with the maximum and minimum ordinate. The remaining candidates for the answer are tangents from the roses to the convex shell of the cherries.
You can directly check all the direct candidates for response. The most difficult thing in this is to construct a tangent to a convex hull from a given point. To do this, you can iterate through all the vertices of the convex hull. The total asymptotic behavior of such a solution will be O (mn), and the program implementing this approach does not fit into the time constraints.
You can think of a more efficient method for finding a tangent. We propose to use another observation. Suppose that the interesting angle of the tangent from this point to the convex figure is β. Let β ≤ α ≤ π / 2. Then one of the tangents to this figure with an interesting angle α, separates this figure and point.
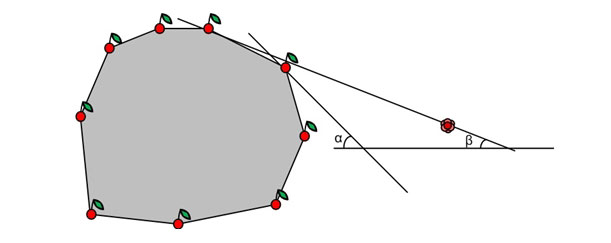
Using the last observation, one can check whether there exists a good straight line, the interesting angle of which does not exceed α. To do this, draw all the tangents to the convex hull of the cherries that have an interesting angle α. After that, we check that there is at least one rosette, such that, relative to one of the tangents, it and the cherries lie on opposite sides. This is easy to do in linear time.

If at least one rosette is not in a darkened area, then the answer is no more than α. The reverse is also true.
After that, the desired angle can be found by binary search.
As a result, we obtain a solution with the asymptotics O (N (log N + I)), where N = n + m, and I is the number of iterations of the binary search.
See you at the Russian Code Cup 2012!
Team Russian Code Cup.

The winner was Peter Mitrichev from Moscow. He received a prize of 10 thousand dollars. USA. The second place was taken by Evgeny Kapun from St. Petersburg, he received $ 5,000. In third place is Mikhail Dvorkin from St. Petersburg with a prize of $ 3,000. Congratulations to the guys and wish them continued success!
')
In this article we will analyze the tasks from the final round.
A complete description of the tasks can be found here .
Problem A. Clock Translation
In this task, the rules for converting hours in several cities were set and it was required to find out the total inconvenience of residents of all cities, where the inconvenience for a couple of cities was determined as the time difference in these cities and these values were required to be summed over all hours in a year.
First, we note that one of the specified cities was the capital, and in the capital, time is not translated. Therefore, it is convenient to choose the Moscow time as the “absolute scale” of reference and use it to indicate the time of all events. First of all, let's go through all the clock translations specified in the input file and for each clock translation we define its time in the absolute scale. Now, each clock translation is characterized by three numbers:
• time on an absolute scale when it occurs,
• the city where the transfer takes place,
• the amount of translation hours.
Now we will consider the events in the order in which they occur on an absolute scale. All the time from the previous to the current event, the inconvenience in the country was constant.
Let's see how much the inconvenience has changed in the country as a result of a change in time in a certain city. Let the city have a shift of i hours relative to the capital. Let the total shift of cities that have a smaller time shift be S, and their number be L. Then the additive to the inconvenience with these cities for the current one is
For a quick calculation of the total time shift in cities on a certain segment of shifts, as well as to count the number of cities in a segment, you can use, for example, a segment tree or a Fenwick tree.
Problem B. Reverse bug problem
In this task, it was required for a given number k to build a maze in which the number of paths from the left upper to the lower right cell, provided that it was allowed to move only to the right and down, would be equal to k.
Note the following. Suppose we have two mazes in which the number of ways to get from the top left to the right bottom cell is a and b, respectively.
Then, placing them in parallel, as shown in the figure, we can get a maze in which a + b ways to get from the top left to the bottom right cell, and by placing them sequentially, we get a maze in which there are ab paths.

Note that in an empty maze of size 2 × 2 there are two ways, and in a maze of size 1 × 1 - one way. Therefore, by expanding the number k into a binary number system and using the described method, one can get a maze with k paths from the upper left to the right lower cell.
An example of such a maze for k = 19 is shown in the figure.

Note that for each digit of the number k, 5 cells are required horizontally, and 2 60 > 10 18 , therefore, the above scheme allows you to create a maze no larger than 300 × 300 in size, as required by the condition of the problem.
Task C. Splitting a table
In this task, it was necessary to count the number of partitions of the table of zeros and units into 9 parts, so that the number of units in the given five of these parts was even.

Perhaps several approaches to solving this problem, consider one of them. Fix c1, c2, r1 and r2. Note that with an increase in r2 by one, the parity of the number of units in parts A5, A7 and A9 does not change if the line r2 contained an even number of ones and changes otherwise. Therefore, with fixed c1, c2 and r1, it is easy to understand which r2 are suitable - depending on the parity of the number of units in the desired parts when r2 = n - 1 are suitable or such r2 that the number of units in the lines starting from r2 + 1 to n is even, is odd. We get the solution in O (n 3 ), which is still not enough to meet the allotted time limit. However, now a similar reasoning can be applied to c1 and c2. With fixed r1, r2, and c1, an increase in c2 by one changes the parity by exactly the parity of the number of units in column c2. Therefore, fixing r1, putting r2 = n - 1 and fixing c1, it is easy to find the number of values of c2 for which r2 is suitable for an even sum in large lines or for an odd sum.
The asymptotics of this solution is already O (n 2 ), which is sufficient under the given constraints.
Task D. Archiver
There are at least two different approaches to this problem: dynamic programming or a greedy algorithm.
Imagine the process of archiving a sequence in the form of a tree: each character of each of the intermediate sequences will be a vertex of the tree, the children of the vertex will be two characters that are “glued together” in the archiving process to the specified one. The original numbers are written in the leaves, and the task is to record the numbers in all intermediate vertices, and the archiving penalty is equal to the number of vertices that have different numbers in the children.
The solution using dynamic programming is arranged as follows: at each vertex u we will store the minimum total penalty p [u] [x] for the subtree if we write the number x at this vertex. Note that at the vertex it is sensible to write only the number that occurs in one of the leaves in the subtree, therefore the total number of options that should be considered is O (n log n).
Recalculation is carried out as follows: consider the vertex u with children v and w. Suppose we plan to write the value of x. If both values of p [v] [x] and p [w] [x] are defined, then one of the options to put x in u is to put x in both children, the price of this option is p [v] [x] + p [w ] [x]. There is also an option to put x only in one child. Suppose we plan to put x in v, then the cost of this variant is p [v] [x] + minp [w] + 1, where minp [w] is the minimum value of p [w] [y] over all y.
An alternative solution to using DP is a greedy solution: for each vertex we will store a list of all possible values, putting one of which to the top we will get the minimum penalty in the subtree. It turns out that in order to find the optimal set for a vertex, it suffices to try to put only optimal values in its children. Moreover, if the lists of optimal values for children overlap, then you need to take one of these numbers. If they do not intersect, then any of the meanings of each of the children will do.
The proof of the correctness of the above algorithm is left as an exercise.
Problem E. Blackjon
In this task, it is necessary to choose a subset of fractions (cards) so that their sum is equal to one. Thus, this task is a special case of the backpack problem. One possible approach to solving the problem is to bring all the fractions to a common denominator. However, the lowest common multiple (NOC) of all possible denominators is 232,792,560, which is too large a number to further solve the resulting “classical” backpack problem.
To solve the problem, it is necessary to divide it into independent subtasks. To do this, it is necessary to divide fractions into five groups depending on the denominator: fractions with denominators of 11, 13, 17, 19, as well as all other fractions. Note that if the fractions selected from any of these groups do not total an integer, then they cannot be added to fractions from other groups to an integer. This fact is due to the fact that in separate groups there are large simple denominators such that there can be no other denominators that are multiple to them except themselves.
In each group, the sum of the selected fractions must be an integer, even possibly zero. Solving the problem of a backpack for each of the groups, we find out whether it is possible to choose fractions in a group so that we can get a certain integer number. Only integers from −100 to 100 are of interest, since the sum of not more than 100 fractions, each of which does not exceed one in absolute value, does not exceed 100 in absolute value. Also note that the NOC of all possible denominators of the latter group is only 5040, there is a number of possible options for the numerator in the amount does not exceed 1 008 001. This fact allows to solve the problem of a backpack in each group in the allotted time.
Knowing which integers can be obtained in each of the groups, it is necessary to check whether by choosing one whole number in each of the groups to get an amount equal to one. This problem can be solved using the dynamic programming method. Let us introduce the value a i , j - is it possible, using the first i groups of fractions, to get the sum exactly j. The base will be the value of a 0 , 0 = true and a 0 , j = false for j from −100 to 100 except zero. The transition is as follows: a i , j = true, if at least for one k is true (a i-1 , jk and b i, k ), and false otherwise, where b i, k is a value that indicates whether group i choose fractions with sum k. The answer to the problem will be the value of a 5,1 .
To find the set of fractions that must be taken, it suffices to use the found values of the dynamics, and for each of the groups to use the standard answer recovery method for the backpack problem.
Problem F. Cutting the cake
Let's call a straight line a good one if the cut along it divides the cake into two pieces, such that there is not a single cherry on one of them and there is at least one rosette. In addition, we call interesting the angle that a straight line forms with the axis Ox. It is required to find the minimum interesting angle of a good straight line.
Consider a good line with a minimal interesting angle. Such a straight line exists, since according to the condition of the problem, when passing a straight line through roses and cherries, one can choose which piece they belong to. Otherwise, a straight line, which is an extremum point, could not exist. The following is true: either this straight line is horizontal, or it passes through a cherry and a rose. Indeed, if a good straight line is not horizontal and does not pass through a cherry or a rose, then it can be slightly rotated in the direction of decreasing the interesting angle so that it remains good. The latter contradicts the minimality condition for an interesting angle.
Check if there is a good horizontal straight is simple enough. To do this, check the horizontal lines passing through the cherries with the maximum and minimum ordinate. The remaining candidates for the answer are tangents from the roses to the convex shell of the cherries.
You can directly check all the direct candidates for response. The most difficult thing in this is to construct a tangent to a convex hull from a given point. To do this, you can iterate through all the vertices of the convex hull. The total asymptotic behavior of such a solution will be O (mn), and the program implementing this approach does not fit into the time constraints.
You can think of a more efficient method for finding a tangent. We propose to use another observation. Suppose that the interesting angle of the tangent from this point to the convex figure is β. Let β ≤ α ≤ π / 2. Then one of the tangents to this figure with an interesting angle α, separates this figure and point.

Using the last observation, one can check whether there exists a good straight line, the interesting angle of which does not exceed α. To do this, draw all the tangents to the convex hull of the cherries that have an interesting angle α. After that, we check that there is at least one rosette, such that, relative to one of the tangents, it and the cherries lie on opposite sides. This is easy to do in linear time.

If at least one rosette is not in a darkened area, then the answer is no more than α. The reverse is also true.
After that, the desired angle can be found by binary search.
As a result, we obtain a solution with the asymptotics O (N (log N + I)), where N = n + m, and I is the number of iterations of the binary search.
See you at the Russian Code Cup 2012!
Team Russian Code Cup.
Source: https://habr.com/ru/post/129047/
All Articles