Stored procedures. Who is faster

What are we talking about

Choosing one or another DBMS for a project as one of the factors influencing the choice is considered the presence of a language of stored procedures and functions, its capabilities, convenience.

What about speed? It is clear that the core of the DBMS is responsible for the sampling rate, making up the query plan, optimizers, the presence of indices, etc. But it's not about that.
The languages ​​of the stored procedures of modern DBMS have many of the properties inherent in classical programming languages: the presence of types and variables, cycles. That's about their speed and talk.

If you are interested in how to calculate the Pi number in three different DBMS or recall a computer science course for the first course, then look under the cat.

')

A bit of math

Recalling the institute youth, the theory of series, it was decided to program the computational problem using mathematical dependencies:




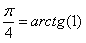
Actually, we will calculate the arctangent, the calculation accuracy is 10 ^-7 .

Firebird

create or alter procedure ARCTG (X double precision) returns (S double precision, I integer) as declare variable U double precision; begin S = X; U = X; I = 3; while (abs(U) >= 0.0000001) do begin U = -U*X*X*(I-2)/I; S = S + U; I = I + 2; end suspend; end 

Here S is the arctangent value, I is the number of iterations multiplied by 2 (approximately).
In the procedures of other systems, variable I was not derived, since the number of iterations will be the same everywhere.
After programming the procedure, we do

 select 4*S,I from arctg(1) 

We get our pi number and the counter value I = 10 000 003, from which we conclude that about 5 million cycles are needed to achieve the required accuracy. Time - 13.5 s.

Mysql

 CREATE DEFINER = 'root'@'localhost' FUNCTION ARCTG(X DOUBLE) RETURNS DOUBLE BEGIN DECLARE U DOUBLE DEFAULT X; DECLARE S DOUBLE DEFAULT X; DECLARE I INT DEFAULT 3; WHILE (abs(U) >= 0.0000001) DO SET U = -U*X*X*(I-2)/I; SET S = S + U; SET I = I + 2; END WHILE; RETURN S; END 

The result is 42.5 c

MsSQL

 CREATE FUNCTION [ARCTG] (@X real=1) RETURNS real WITH EXECUTE AS CALLER AS BEGIN DECLARE @S AS REAL DECLARE @U AS REAL DECLARE @I AS INT SET @S = @X SET @U = @X SET @I = 3 WHILE (abs(@U) >= 0.0000001) BEGIN SET @U = -@U*@X*@X*(@I-2)/@I SET @S = @S + @U SET @I = @I + 2 END RETURN @S; END 

Result - 12 seconds

Results

1. MsSQL 2005 - 12 seconds
2. Firebird 2.5 - 13.5 seconds
3. MySQL 5.1 - 42.5 seconds

All tests were performed on the Athlon 3200+, OS - windows XP.
The result from MySQL surprised. Perhaps the problem was that he walked in the Vertrigo set and was not configured in an optimal way. If someone conducts similar tests, it will be interesting to know.

Well, finally

The time of the C code (Borland compiler, I will not give the code) was about 200 ticks (GetTickCount function), i.e. about 0.2 s. After that there was a thought to transfer the topic to “Abnormal programming”, but I still post it here with the following contradictory conclusions (which one I like):
1. You should not perform large and complex calculations with the help of DBMS mechanisms, although they can do this, but carry the logic out of the DBMS limits.
or
2. DBMS engines have something to strive for.