Calculate the number of pi by the Monte Carlo method

There are many ways to calculate the number of pi. The simplest and most understandable is the Monte Carlo numerical method, the essence of which is reduced to the simplest enumeration of points in the square. The essence of the calculation lies in the fact that we take a square with a side a = 2 R, enter a circle with radius R in it. And we start randomly to put points inside the square. Geometrically, the probability P ₁ that the point falls into a circle is equal to the ratio of the areas of the circle and the square:
P ₁ = S _circle / S _square = πR ² / a ² = πR ² / (2 R) ² = π R ² / (2 R ) ² = π / 4 (1)
It looks like this:



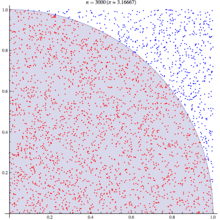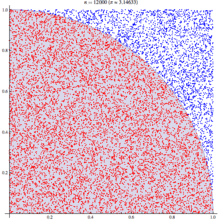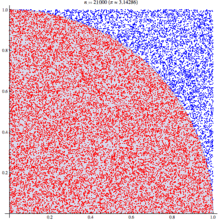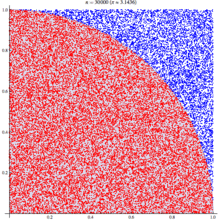
The probability of hitting a point in a circle can also be calculated after a numerical experiment: it is even simpler: calculate the number of points in a circle and divide them by the total number of points set:
P ₂ = N _{caught in the circle} / N _points ; (2)
So, with a large number of points in a numerical experiment, the probabilities should behave as follows:
lim _{(N points → ∞)} (P2-P1) = 0; (3)
Consequently:
π / 4 = N _{caught in the circle} / N _points ; (four)
π = 4 N get to the circle / N _points ; (five)
BUT! In the simulation, we use pseudo-random numbers that are not a random process.
Therefore, expression (5), unfortunately, is not strictly fulfilled. Questions are logical, what are the optimal sizes of the square and how much do you need to apply the points?
To find out, I wrote this program:

#include<stdio.h> #include<math.h> #define limit_Nmax 1e7 //   #define limit_a 1e6 //   #define min_a 100 //  double circle(double, double); //  y        . int main() { double x,y,Pi; long long int a=min_a//  i=0;// double Ncirc=0;// ,    double Nmax=a; //   while (a<limit_a) //   { Nmax=a; while (Nmax<=limit_Nmax) //     { Ncirc=0; i=0; // while (i<Nmax) { x = (random() % (a * 1000))/1000; //   3    y = (random() % (a * 1000))/1000; // Y  3    if (y*y<=circle(x,(a/2))) //     { Ncirc++; } i++; } Pi=(Ncirc/Nmax)*4; Nmax *= 2; printf("\n%lld,%.0f,%f",a,Nmax,Pi); } a*=2; } } double circle(double x, double radius) { double y=radius*radius-x*x; return y; } 

The program displays the values ​​of pi depending on the radius and the number of points. The only thing that remains for the reader is to compile it yourself and run it with the parameters that he wants.

I will give only one table with the obtained values:

Radius	Ntochek	Pi
102400	204800	3.145664
102400	409600	3,137188
102400	819200	3,139326
102400	1638400	3.144478
102400	3276800	3,139875
102400	6553600	3.142611
102400	13107200	3,140872
102400	26214400	3.141644
102400	52428800	3.141217
102400	1,05E + 08	3,141324
102400	2.1E + 08	3.141615
102400	4.19E + 08	3.141665
102400	8,39E + 08	3.141724
102400	1.68E + 09	3.141682

')
If that, the value of Pi can be viewed with an accuracy of a certain sign here .
Source image - Wikipedia.