On the theory of social balance
Hello habr.
Today I want to tell you about the theory of F. Haider’s cognitive balance .
The theory itself belongs to the class of theories of cognitive correspondence . With the help of this class of theories, one can try to mathematically describe social interactions, including in social networks.
The theory of cognitive balance says that a person is always in a state of balance with respect to the world around her, or is striving for it in all possible ways.
The original model names the name of the POX model and consisted of the following components:
')
According to this theory, the PO ratio is also defined through the PX and OX relationships as follows:

For example (from wikipedia) if P likes O; P does not like X; P knows that X created O; can lead P according to this theory to the following possible conclusions:
Based on this model, we can build something of our own, gradually complicating the resulting.
So, suppose that:
If we designate the subjects through the vertices of the graph, and the relations between them through arcs, then we can consider the following triad.

Now suppose that a relationship can only be positive (+) and negative (-).
Then we can 8 possible states of our model.

There is a statement that the triad is harmonious, or stable, if the product of the signs of its connections is a positive number. That is, it is possible in the case when we have 3 positive connections, or two negative and one positive. That is, cases 1,4,6,7 are harmonious and stable, and cases 2, 3, 5, 8 are unstable.
In the form of a table it will look like this.

Unbalanced triads will strive to become balanced. Each of them has three possible scenarios. We get the so-called transition cube.
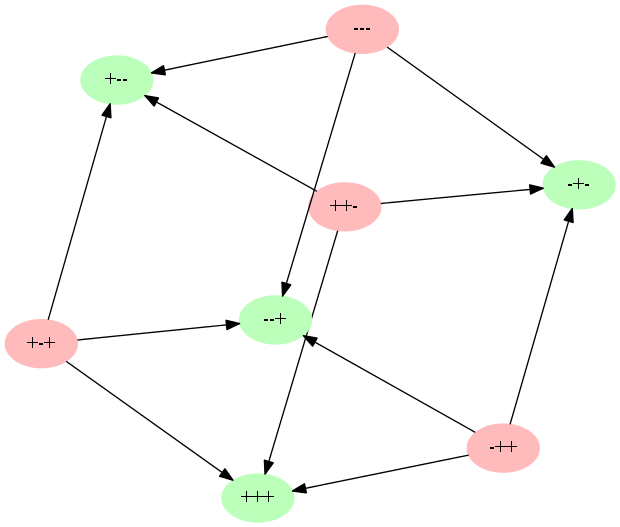
Moreover, the options for the development of a triad are equally likely.
If neutral links are added inside the triad, the number of possible states will increase to 27. In this case, 19 of them will be degenerate cases when not all relationships are established. In this case, the missing links will either not be involved at all or will tend to the balanced ones described above. Given this information, the transition cube will look like this.

That is, as in the first case, we obtain a binary tree of triads and transitions between them.
If the weights of the relations are not equal to each other, then the probabilities of transition from one state to another will be different, and we can predict how the relations inside the triad will change.
But isolated triads, like spherical horses in vacuum, can only be on paper. In the real world, we have a more or less large team, within which interactions are built on the same principle as within the triads. In this case, the balance of the group is determined by the balance of all its triads.
Of the two states of the groups, it is more balanced, in which a greater number of balanced triads.
To assess the balance of the group, you can enter a special index:
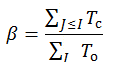
Where T is the number of balanced triads, T is the total number of triads.
Large related subgroups with a high index of balance within groups can be represented as a separate enlarged subject that has relationships with all other subjects.
There is a structural theorem that states that a large graph (a group of people, objects, relations between them) is in a balanced state if and only if a large group is divided into two small subgroups, within which all connections are positive and the connections between groups are negative.
Indeed, if one subgroup is mentally divided into two connected ones with a large positive index, and the second subgroup is left as it is, then a classical balanced triad with one plus and two minuses will turn out. One can speculate on the fact that all subjects can have positive relationships with each other, but the probability of such an outcome is 3 times lower than when divided into two competing subgroups (triad No. 1 and triad No. 4, 6, 7, respectively).
If we assume that there are N people in the group, then the number of possible relations between them will be
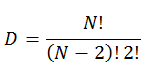
Provided that our relations can be positive (+), negative (-) and neutral (0), the number of all possible states will be
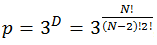
where the total number of triads will be

It should also be borne in mind that spontaneous transitions, other things being equal, are subject to the following rules.
Given these conditions, the next transition cube works for the triad.
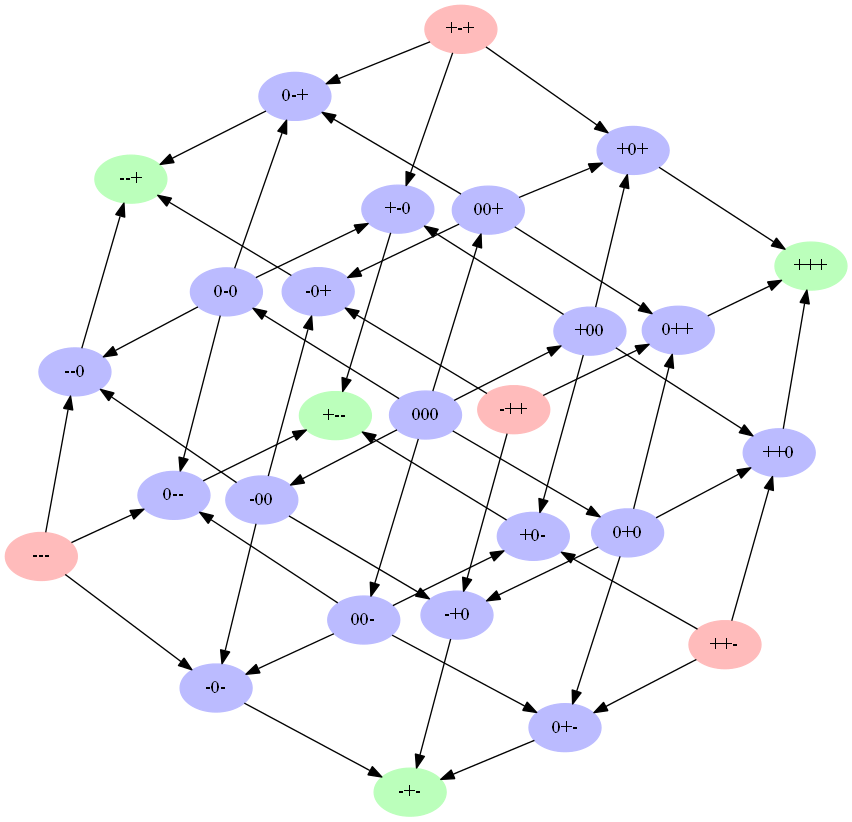
Spontaneous transitions are also affected by the number of balanced triads in which a person takes part. He seeks to move to the state in which the number of his balanced triads increases. In this case, to determine the likelihood of such a transition, a local link balance index is used. Obviously, one relationship cannot take part in all possible triads of a group. Therefore, only those triads are used for evaluation in which this link is involved.
Then we get

where Tc is the balanced triad for this connection, Tloc is the total number of triads for this connection. The principle of evaluation is the same as for the whole group.
For completeness, you can add a smoother change in the relationship - not just positive, negative or zero, but also with some weight r contained in a certain interval. For example, in the interval from -R to R, where R = 0.5; 1; 5; 10 ... In this case, you should set the law according to which the change of these relations takes place. In a number of works, hysteresis is used for these purposes. Other works take into account the concept of social distance.
In this case, you can write a law that changes a relationship over time.

where G (r, R) = (1- (r / R)) ^ 2, and r (i, j) is the relation between the ith and jth subjects.
As a bonus, several animated gifs.
At the bottom of each image displays the overall index balance.
For a simple triad.
Even despite the small initial contradictions, all three are friendly.

Two are friends against the third.

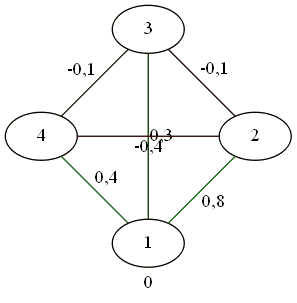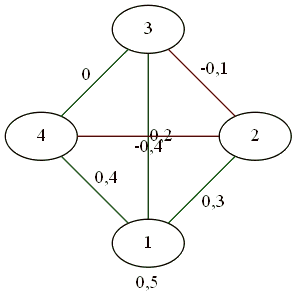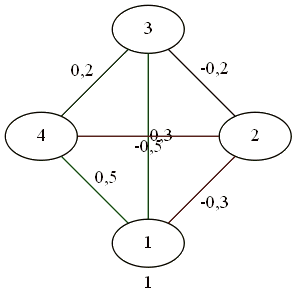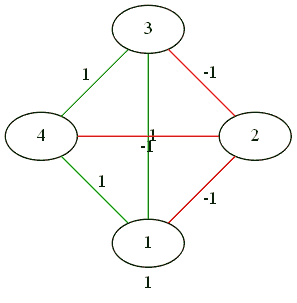
For the four.
Everyone is friends with everyone.

Confrontation 2 by 2.
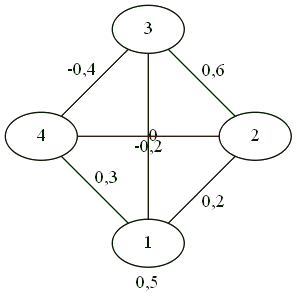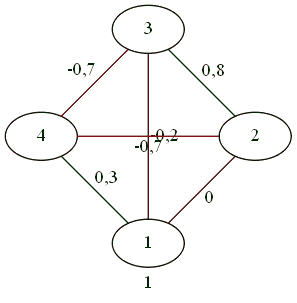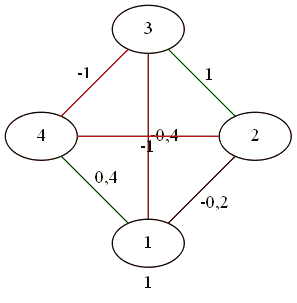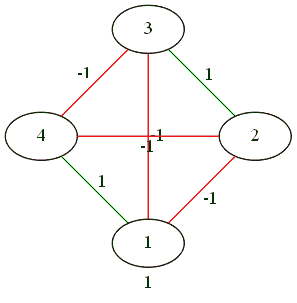
As a result of complex gestures, three against one.
In order not to litter the article, other examples can be found in my album (for 5, 6, 10, and 25).
I want to warn you that for a large number of people there were weighty gifs under 10 MB.
And one more note. The prototype program was written in C #, Graphviz was used for visualization.
Also, when calculating triads, one can take into account the state of the neighbors of the second, third, and higher orders. To break up into clusters, to merge clusters into one big person. It is possible to take into account the fact that we do not always know all the information about the relations between these or other subjects. Or some of the subjects themselves do not have the fullness of information. We can also use some kind of external influence, or assume that the arcs may have different weights, or one of the people has the resources to maintain stable good relations with some other person. Or their absence. You can consider an example of survival from an initially balanced group, and so on.
In the end, we can return to the original model and use the digraph, that is, the relations between the subjects become asymmetric. In this case, the number of arcs doubles, but the principles of calculation remain the same.
However, all this is already a topic of much more serious research.
If it is interesting to someone to read on the topic, then here is a set of references to work, starting from which I made this article.
I have it all. Thanks for attention.
Reference 1
Reference 2
Reference 3
Reference 4
Reference 5
Today I want to tell you about the theory of F. Haider’s cognitive balance .
The theory itself belongs to the class of theories of cognitive correspondence . With the help of this class of theories, one can try to mathematically describe social interactions, including in social networks.
The theory of cognitive balance says that a person is always in a state of balance with respect to the world around her, or is striving for it in all possible ways.
Prologue
The original model names the name of the POX model and consisted of the following components:
')
- P is some personality;
- O is a certain object (including a person), in relation to which this person P is experiencing some kind of relationship in the like / dislike format;
- X is some other person, in relation to which P is experiencing some kind of relationship, and who herself, in relation to the object O, also has some kind of relationship, and P knows about it.
According to this theory, the PO ratio is also defined through the PX and OX relationships as follows:
- My friend's friend is my friend.
- A friend of my enemy is my enemy.
- The enemy of my friend is my enemy.
- The enemy of my enemy is my friend.

For example (from wikipedia) if P likes O; P does not like X; P knows that X created O; can lead P according to this theory to the following possible conclusions:
- X - not so bad
- O - not so good
- X is not the author of O.
Based on this model, we can build something of our own, gradually complicating the resulting.
So, suppose that:
- We have 3 certain subjects: A, B and C.
- All subjects have a relationship to each other, and these relations are mutual (this allows you to move from the digraph to just a graph and simplify the initial model).
If we designate the subjects through the vertices of the graph, and the relations between them through arcs, then we can consider the following triad.

Now suppose that a relationship can only be positive (+) and negative (-).
Then we can 8 possible states of our model.

There is a statement that the triad is harmonious, or stable, if the product of the signs of its connections is a positive number. That is, it is possible in the case when we have 3 positive connections, or two negative and one positive. That is, cases 1,4,6,7 are harmonious and stable, and cases 2, 3, 5, 8 are unstable.
In the form of a table it will look like this.

Unbalanced triads will strive to become balanced. Each of them has three possible scenarios. We get the so-called transition cube.

Moreover, the options for the development of a triad are equally likely.
If neutral links are added inside the triad, the number of possible states will increase to 27. In this case, 19 of them will be degenerate cases when not all relationships are established. In this case, the missing links will either not be involved at all or will tend to the balanced ones described above. Given this information, the transition cube will look like this.

That is, as in the first case, we obtain a binary tree of triads and transitions between them.
If the weights of the relations are not equal to each other, then the probabilities of transition from one state to another will be different, and we can predict how the relations inside the triad will change.
But isolated triads, like spherical horses in vacuum, can only be on paper. In the real world, we have a more or less large team, within which interactions are built on the same principle as within the triads. In this case, the balance of the group is determined by the balance of all its triads.
Of the two states of the groups, it is more balanced, in which a greater number of balanced triads.
Some formulas
To assess the balance of the group, you can enter a special index:
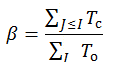
Where T is the number of balanced triads, T is the total number of triads.
Large related subgroups with a high index of balance within groups can be represented as a separate enlarged subject that has relationships with all other subjects.
There is a structural theorem that states that a large graph (a group of people, objects, relations between them) is in a balanced state if and only if a large group is divided into two small subgroups, within which all connections are positive and the connections between groups are negative.
Indeed, if one subgroup is mentally divided into two connected ones with a large positive index, and the second subgroup is left as it is, then a classical balanced triad with one plus and two minuses will turn out. One can speculate on the fact that all subjects can have positive relationships with each other, but the probability of such an outcome is 3 times lower than when divided into two competing subgroups (triad No. 1 and triad No. 4, 6, 7, respectively).
If we assume that there are N people in the group, then the number of possible relations between them will be
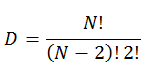
Provided that our relations can be positive (+), negative (-) and neutral (0), the number of all possible states will be
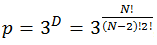
where the total number of triads will be

It should also be borne in mind that spontaneous transitions, other things being equal, are subject to the following rules.
- The probability of spontaneous transition of relations (0) → (+) and (0) → (-) is close to unity.
- The probability of a spontaneous transition of relations (+) → (0), (-) → (0), (+) → (-), (-) → (+) is close to zero.
Given these conditions, the next transition cube works for the triad.

Spontaneous transitions are also affected by the number of balanced triads in which a person takes part. He seeks to move to the state in which the number of his balanced triads increases. In this case, to determine the likelihood of such a transition, a local link balance index is used. Obviously, one relationship cannot take part in all possible triads of a group. Therefore, only those triads are used for evaluation in which this link is involved.
Then we get

where Tc is the balanced triad for this connection, Tloc is the total number of triads for this connection. The principle of evaluation is the same as for the whole group.
For completeness, you can add a smoother change in the relationship - not just positive, negative or zero, but also with some weight r contained in a certain interval. For example, in the interval from -R to R, where R = 0.5; 1; 5; 10 ... In this case, you should set the law according to which the change of these relations takes place. In a number of works, hysteresis is used for these purposes. Other works take into account the concept of social distance.
In this case, you can write a law that changes a relationship over time.

where G (r, R) = (1- (r / R)) ^ 2, and r (i, j) is the relation between the ith and jth subjects.
Examples
As a bonus, several animated gifs.
At the bottom of each image displays the overall index balance.
For a simple triad.
Even despite the small initial contradictions, all three are friendly.

Two are friends against the third.

For the four.
Everyone is friends with everyone.

Confrontation 2 by 2.

As a result of complex gestures, three against one.

In order not to litter the article, other examples can be found in my album (for 5, 6, 10, and 25).
I want to warn you that for a large number of people there were weighty gifs under 10 MB.
And one more note. The prototype program was written in C #, Graphviz was used for visualization.
Also, when calculating triads, one can take into account the state of the neighbors of the second, third, and higher orders. To break up into clusters, to merge clusters into one big person. It is possible to take into account the fact that we do not always know all the information about the relations between these or other subjects. Or some of the subjects themselves do not have the fullness of information. We can also use some kind of external influence, or assume that the arcs may have different weights, or one of the people has the resources to maintain stable good relations with some other person. Or their absence. You can consider an example of survival from an initially balanced group, and so on.
In the end, we can return to the original model and use the digraph, that is, the relations between the subjects become asymmetric. In this case, the number of arcs doubles, but the principles of calculation remain the same.
However, all this is already a topic of much more serious research.
If it is interesting to someone to read on the topic, then here is a set of references to work, starting from which I made this article.
I have it all. Thanks for attention.
Reference 1
Reference 2
Reference 3
Reference 4
Reference 5
Source: https://habr.com/ru/post/128366/
All Articles