Building a digital filter with finite impulse response

Entry from afar

Recently, I faced an interesting task, which I had never come across before - the fight against noise. We took the signal from the sensors to an analog-to-digital converter (ADC)
And since this topic was for me (although there is now somewhere) a dark forest, I went to torment Google with questions, it seemed to me that this topic was not very detailed and accessible, so I decided to write an article with a development example and a ready source.

Closer to the point

Digital filters can be of two types - with finite and with infinite impulse response (FIR and IIR). To solve my problem, an FIR filter is suitable, so I’ll tell you about it.

First, let's see how it works:
')


Here is an example of a low-pass filter, as seen in the figure, this filter skips low frequencies, while everyone else tries to cut off (suppress), or at least weaken (transition). Deviations in bandwidth and bandwidth suppression are selected depending on the received signal, but when using different weighting functions, certain restrictions may be imposed on them. For example, if the Hamming weight function is used, then these deviations will be equal to each other.
The width of the transition band ∆F depends on the length of the filter and on the weight function (for the Blackman function ∆F = 5.5 | N).

The filter works quite simply: the filter gets the values, using the coefficients converts them and produces the output sequence, then everything is clear with the formula of the filter itself:



It is implemented through a cycle, but wait, but where do we get the necessary coefficients? This is where the dog is buried (and not just one).

Filter options

Naturally, different coefficients are needed for different filters, and for this you need to decide on the filter parameters, this is usually done first theoretically (with a smart view we estimate what our signal frequency is, then the frequencies that need to be screened out), and then we study the frequency response of real measurements how much we were wrong).
We determine with these frequency response the ideal frequency response (which frequencies travel freely, which ones we remove and how much), now we need an ideal impulse response that can be calculated as a Fourier transform of the ideal frequency response:



where H_D (w) is an ideal characteristic.

But you can go in a simpler way - there are already pre-calculated ideal impulse responses, for example, for a low-pass filter, the formula is as follows:




where fc and wc is the cutoff frequency.

So, there is already a little ideal ideal, and we are dealing with practice, and we need a “real” impulse response. To calculate it, we need the weight function w (n), there are several varieties, depending on the requirements for the filter (Hamming, Henning, Blackman, Kaiser, I don’t talk about them, because the article is so big), in our case I use the function Blackman:



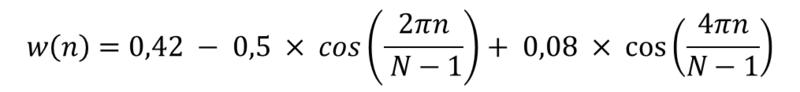
where N is the length of the filter, i.e. the number of coefficients.

Now we need to multiply the ideal impulse response and the weight function:

Finish line

Now we are ready to calculate the output values, according to the formula of the filter, it is the very first in this article, well, that's all, in conclusion, I cite the source code of the filter:

void Filter (const double in[], double out[], int sizeIn) { const int N = 20; //  long double Fd = 2000; //    long double Fs = 20; //   long double Fx = 50; //   long double H [N] = {0}; //   long double H_id [N] = {0}; //   long double W [N] = {0}; //  //    double Fc = (Fs + Fx) / (2 * Fd); for (int i=0;i<N;i++) { if (i==0) H_id[i] = 2*M_PI*Fc; else H_id[i] = sinl(2*M_PI*Fc*i )/(M_PI*i); //    W [i] = 0.42 - 0.5 * cosl((2*M_PI*i) /( N-1)) + 0.08 * cosl((4*M_PI*i) /( N-1)); H [i] = H_id[i] * W[i]; } //   double SUM=0; for (int i=0; i<N; i++) SUM +=H[i]; for (int i=0; i<N; i++) H[i]/=SUM; //   1 //   for (int i=0; i<sizeIn; i++) { out[i]=0.; for (int j=0; j<N-1; j++)//     if(ij>=0) out[i]+= H[j]*in[ij]; } } 

In preparing the article were used:
Main characteristics and parameters of filters. analogiu.ru/6/6-5-2.html
Ifacher E. Jervis B. Digital Signal Processing. Practical approach. 2nd edition