Algorithm analysis

What is analysis?
Analyzing the algorithm, you can get an idea of ​​how long it will take to solve this problem using this algorithm. The same problem can be solved using different algorithms. Analysis of the algorithms gives us a tool to select the algorithm.
The result of the analysis of algorithms is not a formula for the exact number of seconds or computer cycles that a specific algorithm will require. It should be understood that the difference between the algorithm that does N + 5 operations and the one that does N + 250 operations becomes imperceptible as soon as N becomes very large.


Input Classes
When analyzing the algorithm, the choice of input data can significantly affect its performance. Say, some sorting algorithms can work very quickly if the input list is already sorted, while other algorithms will show a very modest result on such a list. But on a random list, the result may be the opposite. Therefore, we will not be limited to analyzing the behavior of algorithms on a single input data set. Practically, you need to look for data that provides both the fastest and the slowest execution of the algorithm. In addition, it is useful to evaluate the average efficiency of the algorithm on all possible data sets.

Best case
')
In the best case, the execution time of an algorithm is often very small or just constant, therefore such an analysis is rarely carried out.

Worst case

The worst case analysis is extremely important because it allows you to imagine the maximum running time of the algorithm. When analyzing the worst case, it is necessary to find the input data on which the algorithm will perform the most work.

Average case

Analysis of the average case is the most difficult because it requires taking into account a variety of different details. The analysis is based on the definition of various groups into which possible input data sets should be broken. In the second step, the probability with which the input data set belongs to each group is determined. In the third step, the running time of the algorithm on the data from each group is calculated. The running time of the algorithm on all input data of one group should be the same, otherwise the group should be subdivided. The average time is calculated by the formula


where n is the size of the input data, m is the number of groups. through pi - the probability that the input data belong to the group with number i, and through ti - the time required for the algorithm to process data from group with number i.

In most cases, we will assume that the probabilities of input data falling into each of the groups are the same. In other words, if there are five groups, then the probability of getting into the first group is the same as the probability of getting into the second, etc., that is, the probability
get into each group is 0.2. In this case, the average time of work can either be estimated by the previous formula, or use the equivalent formula


Lower bounds Decision tree
The algorithm is optimal if any other algorithm that solves this problem works no faster than this one. How to find out the optimality of the algorithm? To do this, we need to know the minimum number of operations necessary to solve the task, which is called the lower bound. But for this we need to study exactly the PROBLEM, and not a specific algorithm!
As an example, consider the analysis of the process of sorting a list of 3 numbers, using a binary tree. Such a tree is called a decision tree.


The longest way in a given tree corresponds to the worst case and vice versa, the shortest way is the best. The average case is described by the particular case of dividing the number of edges in a tree by the number of sheets.
To rearrange 2 elements, we have 1 list, for N elements, according to the rules of combinatorics, N! sheets. The number of sheets at the level of K is 2k-1; therefore, in our decision tree there will be L-levels, where L is the smallest integer for which N! ≤ 2L-1. Logarithm we get



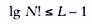
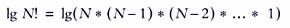
Finally, we get:

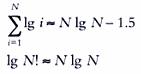
So we learned that any sorting algorithm, order O (NlgN), is the best and can be considered optimal. Moreover, from this study it follows that the algorithm that solves the problem of sorting faster O (NlgN) operations cannot work correctly!