Kosh on the complex plane
On one of the spring days of this year, I rode in a trolleybus and leafed through a Kosh comic . In one of the issues there was such a phrase “BUT! It can be understood, it also flows into the horizon with fractals , I would also hesitate ... ”. After that, I looked out the window and realized that if we take two suitable fractional-linear transformations of the complex plane a ( z ) and b ( z ), and consider the system of iterated functions for a ( z ), b ( z ), a −1 ( z ), b −1 ( z ), taking the Kos image as an initial set, then Kosh will flow fractals into the horizon!
And a few days ago I got around to write the right python script. The results were pleasant to me and my friends , and I decided to write this habrastatyu.
So, if you want to know what fractional-linear transformations of the complex plane are, and how to get fractal images with them, then welcome to Habrakat. There will be a little bit useless mathematics and a lot of gifs.
')
So, take Kosha K and place it on the complex plane:

What can we do with it? For example, we can move in any direction. Such a transformation is written in the form f ( z ) = z + a , where a is some complex number.

We can rotate Kosh at an angle φ relative to the origin. Such a transformation is written in the form f ( z ) = e i φ z .

Finally, we can take and increase Kosh by k times relative to the origin. As it is easy to guess, such a transformation will be written as f ( z ) = kz .

Any linear complex transformation f ( z ) = a z + b can be represented as a composition of these three.
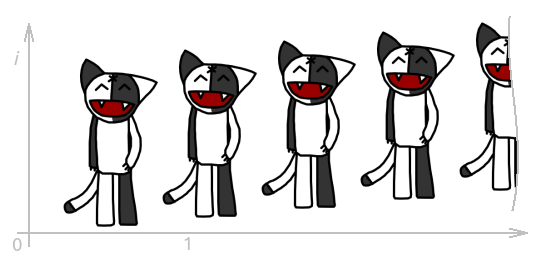
Now let we have some transformation f ( z ). Take the composition of this transformation with itself, get the transformation f ( f ( z )) = f 2 ( z ), then take the composition f ( z ) and f 2 ( z ) get the transformation f ( f 2 ( z )) = f ( f ( f ( z ))) = f 3 ( z ) and so on to infinity. For example, if f ( z ) = z + a , then f n ( z ) = z + na . Applying this series of transformations to our Kosh and combining the result, we get something like this:
But, for example, if we take f ( z ) = k e i φ z (compression with a coefficient k plus a rotation through the angle φ), then we will get a more interesting picture: a spiral from Kosh. (When constructing this picture, the original Kosh was placed so that point 1 was on his chest, k = 0.8, φ = π / 3.)

Let me draw your attention to the fact that the spiral collapses to point 0.
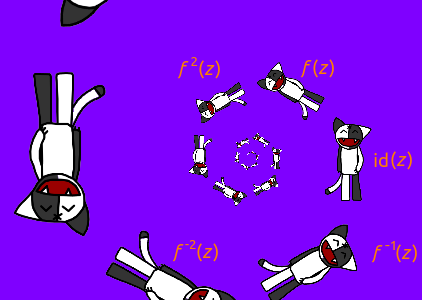
Along with the positive powers of the mapping f ( z ), we can consider zero and negative. With zero, everything is simple - this is the identity mapping: f 0 ( z ) = id ( z ) = z . The negatives are a bit more complicated: you must first reverse the f ( z ) transformation, and then consider the positive powers of the f −1 ( z ) transformation. For the f ( z ) transformation from the previous paragraph, f −1 ( z ) will be a stretch with a coefficient k and a rotation through the angle −φ. Therefore, if Kosh is affected by all integer powers of the f (z) transformation and combines the results, we obtain an infinite in both directions Kosh spiral.
The helix is nice, but let's revive the image a little, for this we note that if you act on the helix with the f ( z ) transformation, nothing will change. Indeed, any of the Kosh fn ( K ) goes into f (fn ( K )) = fn +1 ( K ), but there is such a Kosh in the spiral. And in f n ( K ) Kosh f n −1 ( K ) will go. If we want to make a gif from N frames, then we need to come up with a transformation g ( z ) such that g N ( z ) = f ( z ). But it is simple: g ( z ) = k 1 / N e i φ / N z, that is, g ( z ) compresses N times less and turns an angle N times smaller than f ( z ).

We’ll return to the spiral, and now some fractals. For convenience, we introduce the following notation: t a ( z ) = z + a is the shift by a , r φ ( z ) is the rotation by the angle φ and s k ( z ) is the compression k times. Consider three conversions:
f 1 ( z ) = t i ( r π / 2 ( s 0,6 ( z ))),
f 2 ( z ) = t sqrt (3) / 2 - 0.5 i ( r ( −π / 6 ( s 0.6 ( z ))),
f 3 ( z ) = t −sqrt (3) / 2 - 0.5 i ( r −5π / 6 ( s 0,6 ( z ))).
Suppose the origin is in the center of Kosh, what is the transformation f 1 ( z ) with Kosh? It compresses it almost twice, then puts it on its right side and raises it up by one. (I draw your attention to the fact that the transformations need to be read from right to left.) Something similar is done by the other two transformations - these transformations are chosen so that Kosh’s reduced copies appear at the vertices of a regular triangle.
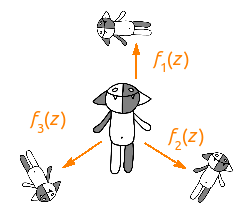
But we do not want to be limited to three Koshs, we need infinitely many of them, so we consider all sorts of compositions of transformations f 1 ( z ), f 2 ( z ) and f 3 ( z ): id ( z ), f 1 ( z ), f 2 ( z ), f 3 ( z ), f 1 ( f 1 ( z )), f 1 ( f 2 ( z )), f 1 ( f 3 ( z )), f 2 ( f 1 ( z )) , f 2 ( f 2 ( z )), f 2 ( f 3 ( z )), f 3 ( f 1 ( z )), f 3 ( f 2 ( z )), f 3 ( f 3 ( z )) , f 1 ( f 1 ( f 1 ( z ))), f 1 ( f 1 ( f 2 ( z ))), ..., f 3 ( f 1 ( f 2 ( f 3 ( f 1 ( z ) )))), ... We will act on Kosh with all this set of transformations, and combine the results. The result is predictable and is shown below.

Add animations again, this time make copies of Kosh rotate around the larger Kosh. How to achieve this? Suppose we want to make N frames, for frame k we consider the corrected transforms f 1 '( z ) = r 2πk / (3N) ( f 1 ( z )), f 2 ' ( z ) = r 2πk / (3N) ( f 2 ( z )), f 3 '( z ) = r 2πk / (3N) ( f 3 ( z )). These transformations differ from the original ones in that they translate Kosh to the vertices of a regular triangle, which is rotated by an angle of 2π k / (3 N ) relative to the original. The result is shown below.

All the transformations above were linear, with the help of them you can’t do much interesting. Consider the transformation: f ( z ) = 1 / z - inversion plus reflection about the real axis. What happens to our Kosh if it is affected by this transformation? If the origin of coordinates is not inside Kosha, then nothing terrible, Kosha must first be inverted relative to the unit circle, and then reflected relative to the real axis, and if 0 is inside Kosha, then it will simply tear it apart (since it is impossible to divide by zero). Below are a few examples.
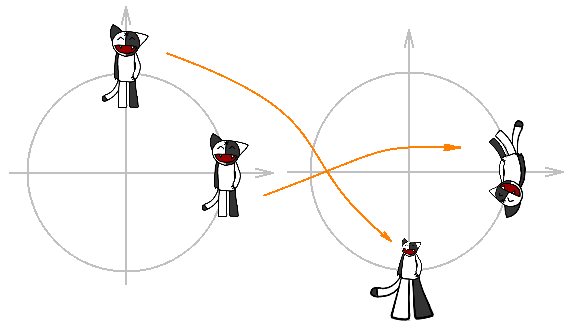
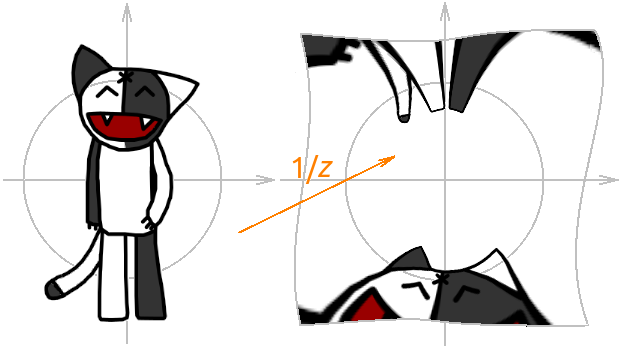
Note that the 1 / z transformation of the exterior of the unit circle translates into the interior of the unit circle, and the interior of the unit circle into exterior.
Now consider the transformations of the form f ( z ) = ( az + b ) / ( cz + d ). Such transformations are called linear fractional . Any such transformation can be represented as a composition already known to us, namely: f ( z ) = f 4 ( f 3 ( f 2 ( f 1 ( z ))), where f 1 ( z ) = z + d / c - shift, f 2 ( z ) = 1 / z - inversion plus reflection, f3 ( z ) = - ( ad - bc ) / c 2 z - compression / tension + rotation, f 4 ( z ) = z + a / c - another shift. Therefore, if some kind of transformation is given, then you can quickly understand what it is doing.
The convenience of considering the transformation in the form of a fraction is as follows: it is very easy to find compositions of fractional-linear transformations and to convert fractional-linear transformations to those who know how to work with matrices. In fact, if the transformation is put into correspondence with a 2 x 2 matrix, in which the coefficients a , b , c , d are arranged in an obvious way, then the composition corresponds to the product of the matrices, and the appeal is the matrix inversion.
The second convenience lies in the fact that immediately by writing you can see at which point the point 0 passes, and at which point - infinity, and also which point goes into 0, and which - at infinity.
Another important property for us is the fact that the straight lines go into straight lines or circles, and the circles too either into straight lines or circles. More precisely: if a line or a circle contains a point that goes to infinity, then it will become a line, otherwise it will become a circle .
Let's return to our spiral. Apply to it a transformation that translates 0 to −1, and infinity to 1: r ( z ) = ( z + 1) / ( z - 1). Since the spiral was wound around zero, now it will begin to wrap around −1, but the spiral still unwound from infinity, so it will begin to unwind from 1.

Consider a polar grid on the complex plane and put Kosha in each cell of this grid.

Consider the transformation f ( z ) = k e i φ z . It rotates the polar grid at an angle φ and compresses all cells k times. If we consider several frames in succession, we get the following:

If we try to keep track of any of the Kosheyas, we will see that it moves along an unwinding spiral, and we have already dealt with it, so it is clear what will happen if we also make the transformation r ( z ) = ( z + 1) / ( z - 1).
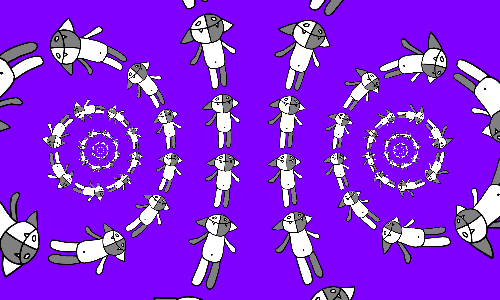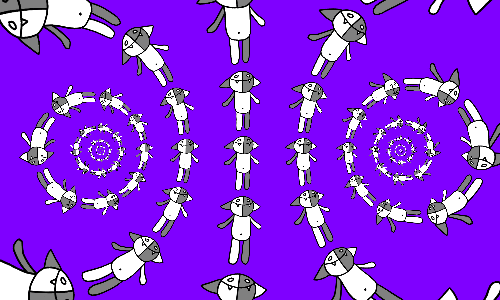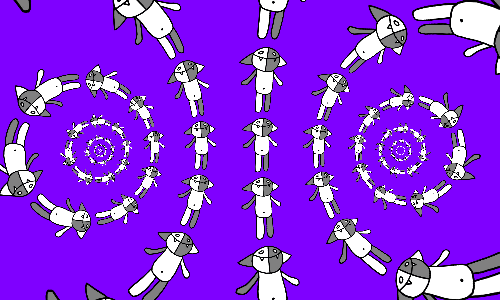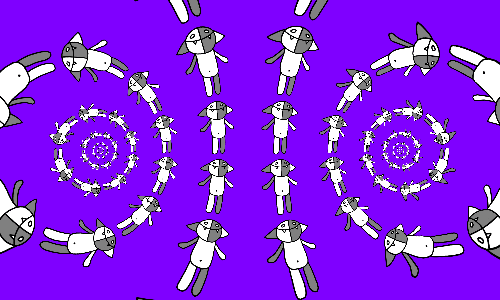
If in each cell of the Kosh grid is laid on its side, then we get a slightly different picture.

The f ( z ) transformation is loxodromic; other types of transformations can also be considered .
We have dealt with one fractional-linear transformation, now you should pour yourself a cup of delicious tea and consider two transformations:
a ( z ) = (sqrt (2) z + 1) / ( z + sqrt (2)),
b ( z ) = (sqrt (2) z + i ) / (- iz + sqrt (2)).
What does a ( z ) do? We decompose it into the composition f 4 ( f 3 ( f 2 ( f 1 ( z ))): f 1 ( z ) = z + sqrt (2) - shift sqrt (2) to the right. F 2 ( z ) = 1 / z - inversion relative to the origin plus reflection relative to the real axis, f 3 ( z ) = - z - rotation by π, f 4 ( z ) = z + sqrt (2) - shift by sqrt (2) to the right. all together, it turns out that the exterior of the unit circle C 1 centered at −sqrt (2) goes into the interior of the unit circle C 2 centered at sqrt (2), and the interior of the circle C 1 becomes the exterior of the circle C 2 .
The transformation a −1 ( z ) acts, as it should be the inverse transformation, exactly the opposite.
The transformation b ( z ) acts similarly - only the circles C 1 and C 2 have centers at the points - i sqrt (2) and sqrt (2).
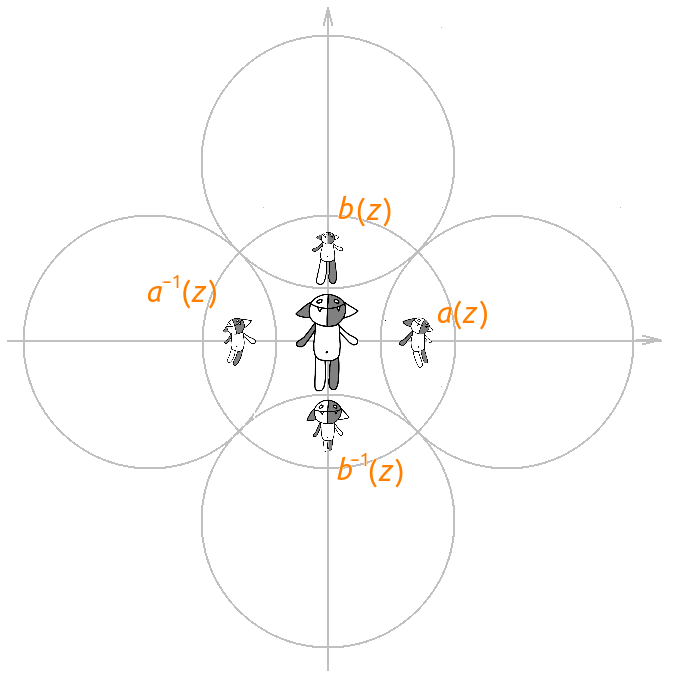
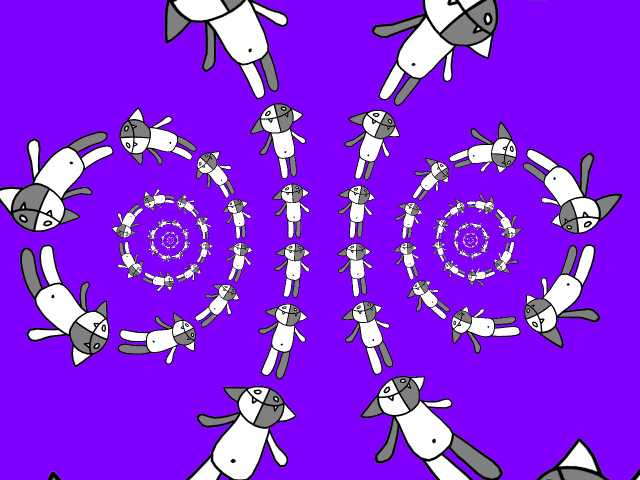
It's time to go to fractals: consider all possible compositions of the maps a ( z ), b ( z ), a −1 ( z ) and b −1 ( z ) and act on Kosh:

To get the gif, we again note that if we apply the transformation a ( z ) or b ( z ) to the resulting picture, nothing will change. Consider, for example, b (z): think up a transformation g ( z ) for which g N ( z ) = b ( z ). This is easy to do, since it is known that the transformation b ( z ) can be represented as b ( z ) = t −1 ( m ( t ( z ))), where t ( z ) = ( z - z 1 ) / ( z - z 2 ), m ( z ) = k e i φ z, and z 1 and z 2 are fixed points of the map b ( z ).
Fixed points are easy to find: we solve the quadratic equation b ( z ) = z and get z 1 = - i , z 2 = i , whence we get m ( z ) = t ( a ( t −1 ( z ))), therefore , m ( z ) = (sqrt (2) + 1) z / (sqrt (2) - 1). Therefore, g ( z ) = t −1 ((sqrt (2) + 1) 1 / N t ( z ) / (sqrt (2) - 1) 1 / N ) = (( q + w ) z / 2 + i ( q - w ) / 2) / (- i ( q - w ) z / 2 + ( q + w ) / 2)), where q = (sqrt (2) + 1) 1 / N , w = (sqrt (2) - 1) 1 / N.
We program and get:
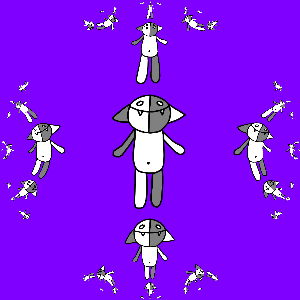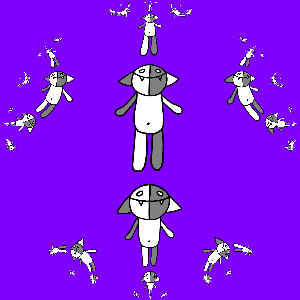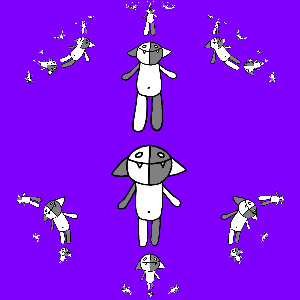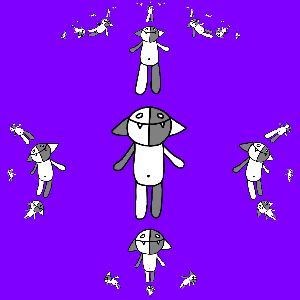
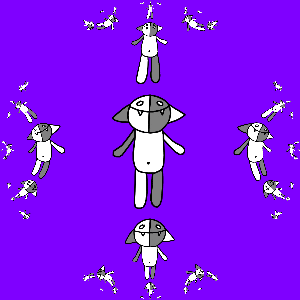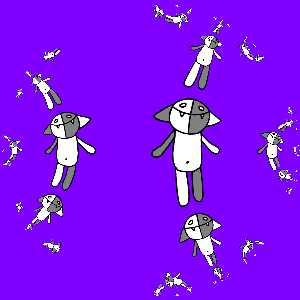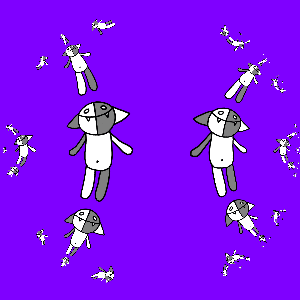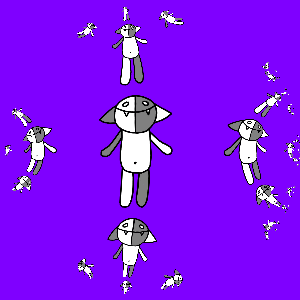
It is interesting to note here that the transformation g ( z ) turned out to be an automorphism of the unit circle.
Finally, if you first apply g ( z ) to Koshu, and then the rest of the mappings, you will also get good:
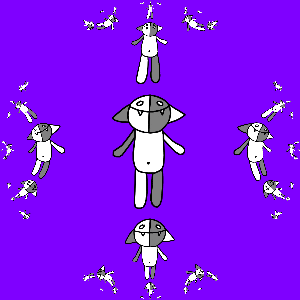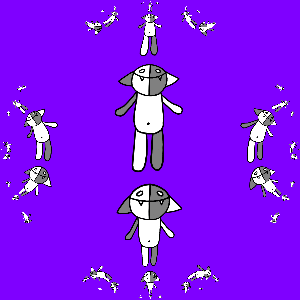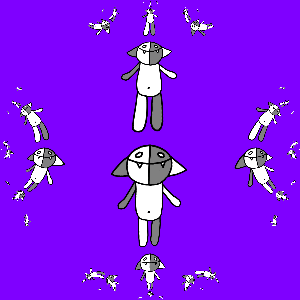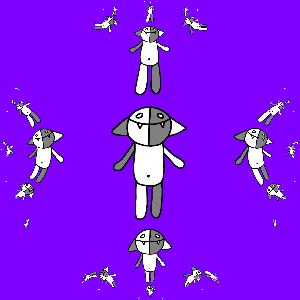
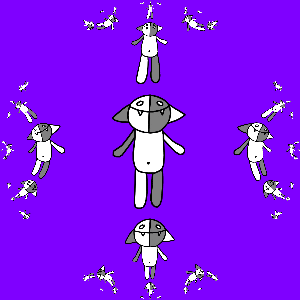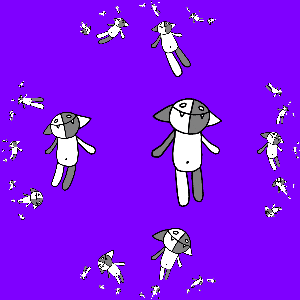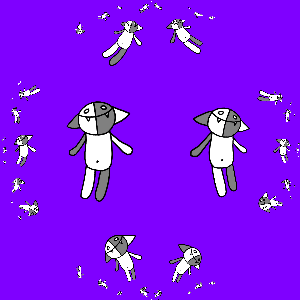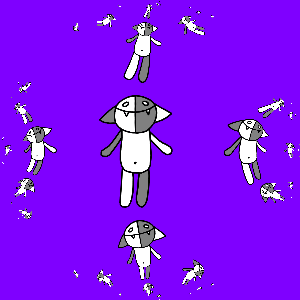
That's all.
If someone wants to know more, I recommend Mumford 's book Indra's Pearls and others.
If someone wants to experiment, the code is laid out on the github .
If someone wants to pozalipat, then you can do it on a coub: one and two times .
And a few days ago I got around to write the right python script. The results were pleasant to me and my friends , and I decided to write this habrastatyu.
So, if you want to know what fractional-linear transformations of the complex plane are, and how to get fractal images with them, then welcome to Habrakat. There will be a little bit useless mathematics and a lot of gifs.
')

So, take Kosha K and place it on the complex plane:

What can we do with it? For example, we can move in any direction. Such a transformation is written in the form f ( z ) = z + a , where a is some complex number.

We can rotate Kosh at an angle φ relative to the origin. Such a transformation is written in the form f ( z ) = e i φ z .

Finally, we can take and increase Kosh by k times relative to the origin. As it is easy to guess, such a transformation will be written as f ( z ) = kz .

Any linear complex transformation f ( z ) = a z + b can be represented as a composition of these three.
Now let we have some transformation f ( z ). Take the composition of this transformation with itself, get the transformation f ( f ( z )) = f 2 ( z ), then take the composition f ( z ) and f 2 ( z ) get the transformation f ( f 2 ( z )) = f ( f ( f ( z ))) = f 3 ( z ) and so on to infinity. For example, if f ( z ) = z + a , then f n ( z ) = z + na . Applying this series of transformations to our Kosh and combining the result, we get something like this:

But, for example, if we take f ( z ) = k e i φ z (compression with a coefficient k plus a rotation through the angle φ), then we will get a more interesting picture: a spiral from Kosh. (When constructing this picture, the original Kosh was placed so that point 1 was on his chest, k = 0.8, φ = π / 3.)

Let me draw your attention to the fact that the spiral collapses to point 0.
Along with the positive powers of the mapping f ( z ), we can consider zero and negative. With zero, everything is simple - this is the identity mapping: f 0 ( z ) = id ( z ) = z . The negatives are a bit more complicated: you must first reverse the f ( z ) transformation, and then consider the positive powers of the f −1 ( z ) transformation. For the f ( z ) transformation from the previous paragraph, f −1 ( z ) will be a stretch with a coefficient k and a rotation through the angle −φ. Therefore, if Kosh is affected by all integer powers of the f (z) transformation and combines the results, we obtain an infinite in both directions Kosh spiral.

The helix is nice, but let's revive the image a little, for this we note that if you act on the helix with the f ( z ) transformation, nothing will change. Indeed, any of the Kosh fn ( K ) goes into f (fn ( K )) = fn +1 ( K ), but there is such a Kosh in the spiral. And in f n ( K ) Kosh f n −1 ( K ) will go. If we want to make a gif from N frames, then we need to come up with a transformation g ( z ) such that g N ( z ) = f ( z ). But it is simple: g ( z ) = k 1 / N e i φ / N z, that is, g ( z ) compresses N times less and turns an angle N times smaller than f ( z ).

We’ll return to the spiral, and now some fractals. For convenience, we introduce the following notation: t a ( z ) = z + a is the shift by a , r φ ( z ) is the rotation by the angle φ and s k ( z ) is the compression k times. Consider three conversions:
f 1 ( z ) = t i ( r π / 2 ( s 0,6 ( z ))),
f 2 ( z ) = t sqrt (3) / 2 - 0.5 i ( r ( −π / 6 ( s 0.6 ( z ))),
f 3 ( z ) = t −sqrt (3) / 2 - 0.5 i ( r −5π / 6 ( s 0,6 ( z ))).
Suppose the origin is in the center of Kosh, what is the transformation f 1 ( z ) with Kosh? It compresses it almost twice, then puts it on its right side and raises it up by one. (I draw your attention to the fact that the transformations need to be read from right to left.) Something similar is done by the other two transformations - these transformations are chosen so that Kosh’s reduced copies appear at the vertices of a regular triangle.

But we do not want to be limited to three Koshs, we need infinitely many of them, so we consider all sorts of compositions of transformations f 1 ( z ), f 2 ( z ) and f 3 ( z ): id ( z ), f 1 ( z ), f 2 ( z ), f 3 ( z ), f 1 ( f 1 ( z )), f 1 ( f 2 ( z )), f 1 ( f 3 ( z )), f 2 ( f 1 ( z )) , f 2 ( f 2 ( z )), f 2 ( f 3 ( z )), f 3 ( f 1 ( z )), f 3 ( f 2 ( z )), f 3 ( f 3 ( z )) , f 1 ( f 1 ( f 1 ( z ))), f 1 ( f 1 ( f 2 ( z ))), ..., f 3 ( f 1 ( f 2 ( f 3 ( f 1 ( z ) )))), ... We will act on Kosh with all this set of transformations, and combine the results. The result is predictable and is shown below.

Add animations again, this time make copies of Kosh rotate around the larger Kosh. How to achieve this? Suppose we want to make N frames, for frame k we consider the corrected transforms f 1 '( z ) = r 2πk / (3N) ( f 1 ( z )), f 2 ' ( z ) = r 2πk / (3N) ( f 2 ( z )), f 3 '( z ) = r 2πk / (3N) ( f 3 ( z )). These transformations differ from the original ones in that they translate Kosh to the vertices of a regular triangle, which is rotated by an angle of 2π k / (3 N ) relative to the original. The result is shown below.

All the transformations above were linear, with the help of them you can’t do much interesting. Consider the transformation: f ( z ) = 1 / z - inversion plus reflection about the real axis. What happens to our Kosh if it is affected by this transformation? If the origin of coordinates is not inside Kosha, then nothing terrible, Kosha must first be inverted relative to the unit circle, and then reflected relative to the real axis, and if 0 is inside Kosha, then it will simply tear it apart (since it is impossible to divide by zero). Below are a few examples.


Note that the 1 / z transformation of the exterior of the unit circle translates into the interior of the unit circle, and the interior of the unit circle into exterior.
Now consider the transformations of the form f ( z ) = ( az + b ) / ( cz + d ). Such transformations are called linear fractional . Any such transformation can be represented as a composition already known to us, namely: f ( z ) = f 4 ( f 3 ( f 2 ( f 1 ( z ))), where f 1 ( z ) = z + d / c - shift, f 2 ( z ) = 1 / z - inversion plus reflection, f3 ( z ) = - ( ad - bc ) / c 2 z - compression / tension + rotation, f 4 ( z ) = z + a / c - another shift. Therefore, if some kind of transformation is given, then you can quickly understand what it is doing.
The convenience of considering the transformation in the form of a fraction is as follows: it is very easy to find compositions of fractional-linear transformations and to convert fractional-linear transformations to those who know how to work with matrices. In fact, if the transformation is put into correspondence with a 2 x 2 matrix, in which the coefficients a , b , c , d are arranged in an obvious way, then the composition corresponds to the product of the matrices, and the appeal is the matrix inversion.
The second convenience lies in the fact that immediately by writing you can see at which point the point 0 passes, and at which point - infinity, and also which point goes into 0, and which - at infinity.
Another important property for us is the fact that the straight lines go into straight lines or circles, and the circles too either into straight lines or circles. More precisely: if a line or a circle contains a point that goes to infinity, then it will become a line, otherwise it will become a circle .
Let's return to our spiral. Apply to it a transformation that translates 0 to −1, and infinity to 1: r ( z ) = ( z + 1) / ( z - 1). Since the spiral was wound around zero, now it will begin to wrap around −1, but the spiral still unwound from infinity, so it will begin to unwind from 1.

Consider a polar grid on the complex plane and put Kosha in each cell of this grid.

Consider the transformation f ( z ) = k e i φ z . It rotates the polar grid at an angle φ and compresses all cells k times. If we consider several frames in succession, we get the following:

If we try to keep track of any of the Kosheyas, we will see that it moves along an unwinding spiral, and we have already dealt with it, so it is clear what will happen if we also make the transformation r ( z ) = ( z + 1) / ( z - 1).

If in each cell of the Kosh grid is laid on its side, then we get a slightly different picture.

The f ( z ) transformation is loxodromic; other types of transformations can also be considered .
We have dealt with one fractional-linear transformation, now you should pour yourself a cup of delicious tea and consider two transformations:
a ( z ) = (sqrt (2) z + 1) / ( z + sqrt (2)),
b ( z ) = (sqrt (2) z + i ) / (- iz + sqrt (2)).
What does a ( z ) do? We decompose it into the composition f 4 ( f 3 ( f 2 ( f 1 ( z ))): f 1 ( z ) = z + sqrt (2) - shift sqrt (2) to the right. F 2 ( z ) = 1 / z - inversion relative to the origin plus reflection relative to the real axis, f 3 ( z ) = - z - rotation by π, f 4 ( z ) = z + sqrt (2) - shift by sqrt (2) to the right. all together, it turns out that the exterior of the unit circle C 1 centered at −sqrt (2) goes into the interior of the unit circle C 2 centered at sqrt (2), and the interior of the circle C 1 becomes the exterior of the circle C 2 .
The transformation a −1 ( z ) acts, as it should be the inverse transformation, exactly the opposite.
The transformation b ( z ) acts similarly - only the circles C 1 and C 2 have centers at the points - i sqrt (2) and sqrt (2).

It's time to go to fractals: consider all possible compositions of the maps a ( z ), b ( z ), a −1 ( z ) and b −1 ( z ) and act on Kosh:

To get the gif, we again note that if we apply the transformation a ( z ) or b ( z ) to the resulting picture, nothing will change. Consider, for example, b (z): think up a transformation g ( z ) for which g N ( z ) = b ( z ). This is easy to do, since it is known that the transformation b ( z ) can be represented as b ( z ) = t −1 ( m ( t ( z ))), where t ( z ) = ( z - z 1 ) / ( z - z 2 ), m ( z ) = k e i φ z, and z 1 and z 2 are fixed points of the map b ( z ).
Fixed points are easy to find: we solve the quadratic equation b ( z ) = z and get z 1 = - i , z 2 = i , whence we get m ( z ) = t ( a ( t −1 ( z ))), therefore , m ( z ) = (sqrt (2) + 1) z / (sqrt (2) - 1). Therefore, g ( z ) = t −1 ((sqrt (2) + 1) 1 / N t ( z ) / (sqrt (2) - 1) 1 / N ) = (( q + w ) z / 2 + i ( q - w ) / 2) / (- i ( q - w ) z / 2 + ( q + w ) / 2)), where q = (sqrt (2) + 1) 1 / N , w = (sqrt (2) - 1) 1 / N.
We program and get:
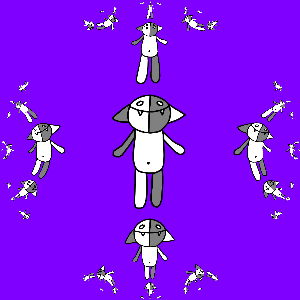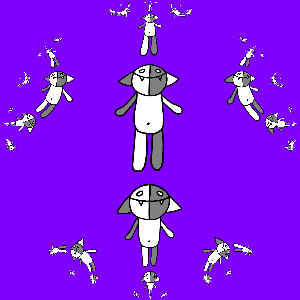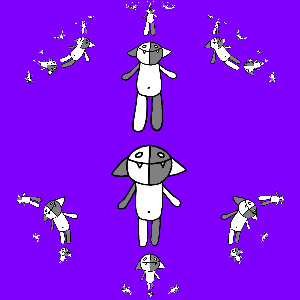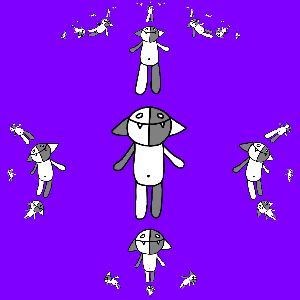
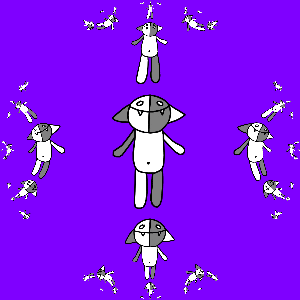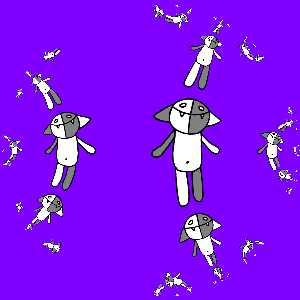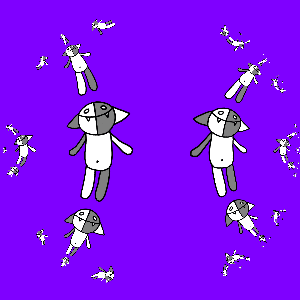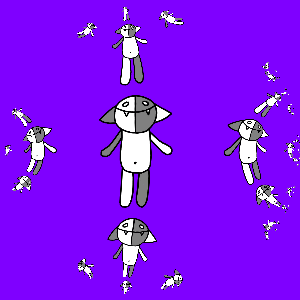
It is interesting to note here that the transformation g ( z ) turned out to be an automorphism of the unit circle.
Finally, if you first apply g ( z ) to Koshu, and then the rest of the mappings, you will also get good:
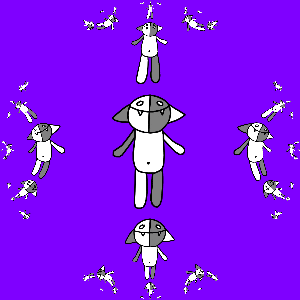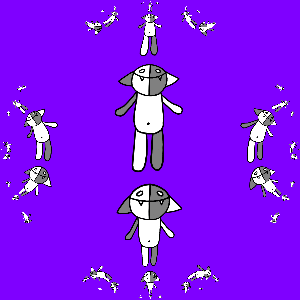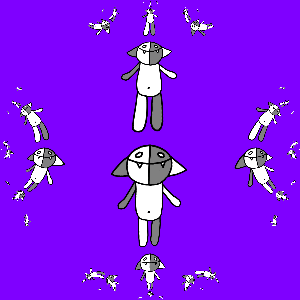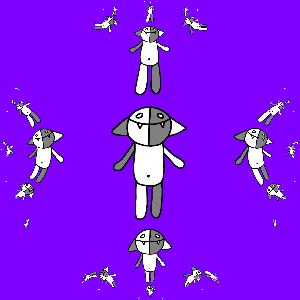
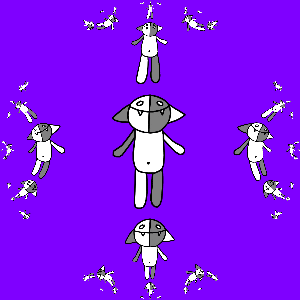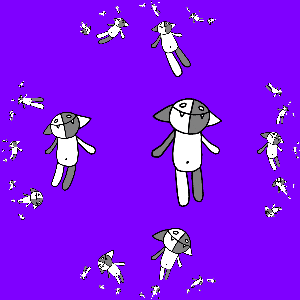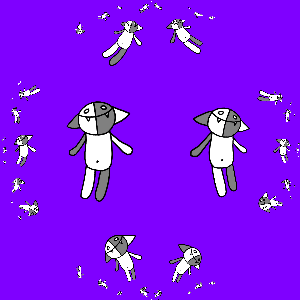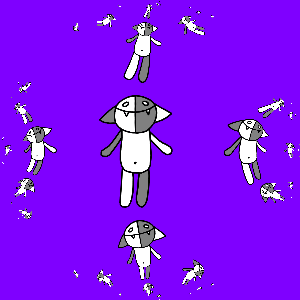
That's all.
If someone wants to know more, I recommend Mumford 's book Indra's Pearls and others.
If someone wants to experiment, the code is laid out on the github .
If someone wants to pozalipat, then you can do it on a coub: one and two times .
Source: https://habr.com/ru/post/126869/
All Articles