The Basics of Fractal Image Compression
Fractals are amazing mathematical objects that captivate with their simplicity and rich possibilities of constructing objects of complex nature with just a few coefficients and a simple iterative scheme.
It is these features that make it possible to use them for image compression, especially for nature photos and other complex self-similar images.
In this article I will try to briefly answer the simple question: “How is this done?”.
For starters, you still have to go a bit into math and enter a few definitions.
We need the following:
Contractive mappings have an important property. If we take any point and begin to apply the same contraction mapping to it iteratively: f (f (f ... f (x))), then the result will always be the same point. The more times we apply, the more accurately we find this point. It is called a fixed point and for each compressing map it exists, and only one.
Several affine compressive mappings form an iterated function system (CIF). In essence, CIF is a copying machine. It takes the original image, distorts it, moves it, and so on several times.
For example, like this, using the CIF, the Sierpinski triangle is constructed from three functions:
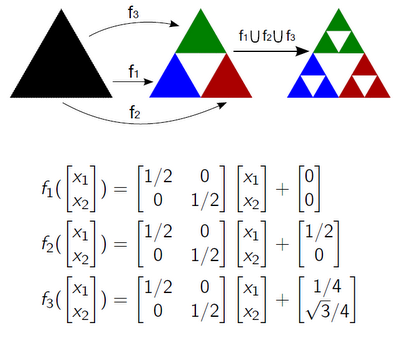
')
The original triangle is multiplied three times, reduced and transferred. And so on. If we continue like this to infinity, we get a known fractal with an area of 0 and a dimension of 1.585.
If the functions included in the CIF are compressive, then the CIF itself also has a fixed point. But this “point” will no longer be a familiar point in N-dimensional space, but a set of such points, that is, an image. It is called the CIF attractor . For the CIF above, the attractor is the Sierpinski triangle.
Here we go to the next level - in the space of images. In this space:
With a CIF, finding an attractor is easy. In any case, having a computer at hand. You can take absolutely any initial image and start applying CIF to it. An example with the same triangle, but already constructed from a square:

It turns out that to build a rather complex shape, we needed 18 coefficients. The win, as they say, is obvious.
Now, if we were able to solve the inverse problem - having an attractor, build a CIF ... Then it is enough to take an attractor-image similar to a photo of your cat and you can encode it quite profitably.
Here, in fact, the problems begin. Arbitrary images, unlike fractals, are not self-similar, so this problem is not solved so easily. Arnold Zhakin invented how to do this in 1992, while he was a graduate student of Michael Barnsley, who is considered the father of fractal compression.
We need self-similarity — otherwise, affine transformations that are limited in their capabilities cannot believably bring images closer. And if it is not between the part and the whole, then you can search between the part and the part. Apparently, Zhakin apparently argued this way.
The simplified coding scheme looks like this:
In the picture, the rank block is marked in yellow, the corresponding domain is marked in red. Also shown are the conversion steps and the result.
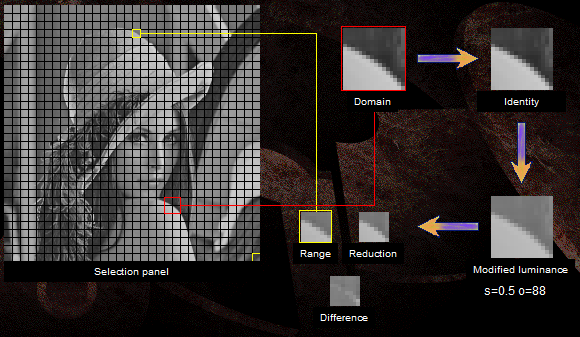
You can play yourself: Coder demo .
Obtaining an optimal transformation is a separate topic, but it is not a big deal. But another drawback of the scheme is visible to the naked eye. You can calculate for yourself how many 32 × 32 domain blocks contains a two-megapixel image. Their exhaustive search for each rank block is the main problem of this type of compression - encoding takes a lot of time. Of course, this is fought with the help of various tricks, such as narrowing the search area or pre-classification of domain blocks. With various damage to quality.
Decoding is done simply and fairly quickly. We take any image, divide by the ranking areas, consistently replace them with the result of applying acc. conversions to acc. domain domain (whatever it contains at the moment). After several iterations, the original image will look like itself:

Perhaps, for the introduction of information is enough. Those interested can read the relevant articles in Wikipedia or the relevant community .
A detailed presentation can be found in this article , from which it all began in 1992. Most of the materials, of course, in English.
It is these features that make it possible to use them for image compression, especially for nature photos and other complex self-similar images.
In this article I will try to briefly answer the simple question: “How is this done?”.
For starters, you still have to go a bit into math and enter a few definitions.
We need the following:
- A metric is a function defined on a space that returns the distance between two points of this space. For example, the Euclidean metric we are used to. If a metric is given on the space, it is called metric. The metric should meet certain conditions, but we will not go deep.
- A contraction mapping (transformation) is a function on a metric space that uniformly reduces the distance between two points in space. For example, y = 0.5x.
Contractive mappings have an important property. If we take any point and begin to apply the same contraction mapping to it iteratively: f (f (f ... f (x))), then the result will always be the same point. The more times we apply, the more accurately we find this point. It is called a fixed point and for each compressing map it exists, and only one.
Several affine compressive mappings form an iterated function system (CIF). In essence, CIF is a copying machine. It takes the original image, distorts it, moves it, and so on several times.
For example, like this, using the CIF, the Sierpinski triangle is constructed from three functions:

')
The original triangle is multiplied three times, reduced and transferred. And so on. If we continue like this to infinity, we get a known fractal with an area of 0 and a dimension of 1.585.
If the functions included in the CIF are compressive, then the CIF itself also has a fixed point. But this “point” will no longer be a familiar point in N-dimensional space, but a set of such points, that is, an image. It is called the CIF attractor . For the CIF above, the attractor is the Sierpinski triangle.
Here we go to the next level - in the space of images. In this space:
- The point of space is an image.
- The distance between the points shows how similar the images are to each other, how “close” they are (naturally, if you set it accordingly).
- Compressive mapping makes two any images more similar (in the sense of a given metric).
With a CIF, finding an attractor is easy. In any case, having a computer at hand. You can take absolutely any initial image and start applying CIF to it. An example with the same triangle, but already constructed from a square:

It turns out that to build a rather complex shape, we needed 18 coefficients. The win, as they say, is obvious.
Now, if we were able to solve the inverse problem - having an attractor, build a CIF ... Then it is enough to take an attractor-image similar to a photo of your cat and you can encode it quite profitably.
Here, in fact, the problems begin. Arbitrary images, unlike fractals, are not self-similar, so this problem is not solved so easily. Arnold Zhakin invented how to do this in 1992, while he was a graduate student of Michael Barnsley, who is considered the father of fractal compression.
We need self-similarity — otherwise, affine transformations that are limited in their capabilities cannot believably bring images closer. And if it is not between the part and the whole, then you can search between the part and the part. Apparently, Zhakin apparently argued this way.
The simplified coding scheme looks like this:
- The image is divided into small non-overlapping square areas, called rank blocks. In fact, it is divided into squares. See picture below.
- A pool of all possible overlapping blocks of four times large rank-domain blocks is built.
- For each rank block, we “try on” the domain blocks in turn and look for such a transformation that makes the domain block more similar to the current rank one.
- A pair of "transformation-domain block", which is close to the ideal, is assigned to the rank block. Transformation coefficients and domain block coordinates are saved to the encoded image. We don’t need the contents of the domain block - you remember, we don’t care from which point to start.
In the picture, the rank block is marked in yellow, the corresponding domain is marked in red. Also shown are the conversion steps and the result.

You can play yourself: Coder demo .
Obtaining an optimal transformation is a separate topic, but it is not a big deal. But another drawback of the scheme is visible to the naked eye. You can calculate for yourself how many 32 × 32 domain blocks contains a two-megapixel image. Their exhaustive search for each rank block is the main problem of this type of compression - encoding takes a lot of time. Of course, this is fought with the help of various tricks, such as narrowing the search area or pre-classification of domain blocks. With various damage to quality.
Decoding is done simply and fairly quickly. We take any image, divide by the ranking areas, consistently replace them with the result of applying acc. conversions to acc. domain domain (whatever it contains at the moment). After several iterations, the original image will look like itself:

Perhaps, for the introduction of information is enough. Those interested can read the relevant articles in Wikipedia or the relevant community .
A detailed presentation can be found in this article , from which it all began in 1992. Most of the materials, of course, in English.
Source: https://habr.com/ru/post/126653/
All Articles