Foreword

This application may not have practical value, but the experience really added a lot. I would like to reflect a little on computer vision. This area is one of the most exciting in modern computer computing, and it is very complex. What is easy and simple for the human brain, it is very difficult for a computer. Many things are still impossible with the current level of IT development.

The program is written using low-level C ++ language, because I really wanted to understand how this all works from the inside. If you also want to start studying computer vision, then the OpenCV library is useful for this. On CodeProject you can find several lessons on it. The image from the webcam is obtained using the source code Vadim Gorbatenko (AviCap CodeProject).

The image below explains how the program works.
')


The time intervals below are delays in milliseconds on my 2.8 GHz PC with a webcam resolution of 640x480. We are seeing an interesting result. For example, the slowest step is getting a frame from the camera. It takes 100 ms, and this means that you will receive only 10 frames per second. It is not enough. Webcams are usually slow. You can speed them up by changing the resolution. Reducing it, you will speed up the shooting, but sacrifice quality, and it may be completely unsuitable for analysis. Another surprise is that converting an image into a binary form (only white or black) also takes a lot of time, as much as 12 ms. On the other hand, I expected the OCR adjustment and the decision of the sudoku itself to take a lot of time, and I was pleasantly surprised when it turned out that these steps are performed together in 8 ms. Below I will explain each step in detail and show what can be improved.

How does the conversion to a monochrome image

Threshold selection

Each computer vision application starts by converting a color (or black and white) image into a monochrome. In the future, there may be some kind of algorithm that will use colors, but today computer vision applications work with monochrome images (they are color blind).

The easiest method to convert an image is a common threshold. Suppose you have a pixel with the color RGB (200, 200, 200). Since the intensity of the components varies from 0 to 255, the pixel is very bright. Choosing the threshold as half the intensity: 256/2 = 128, we get that our pixel should turn white. But the common threshold is rarely used in real applications, as it is of little use. Much more useful is the local threshold algorithm.



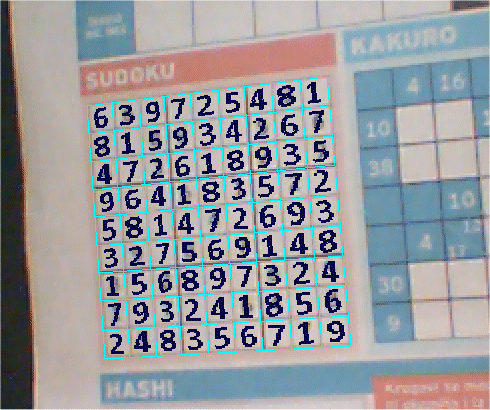
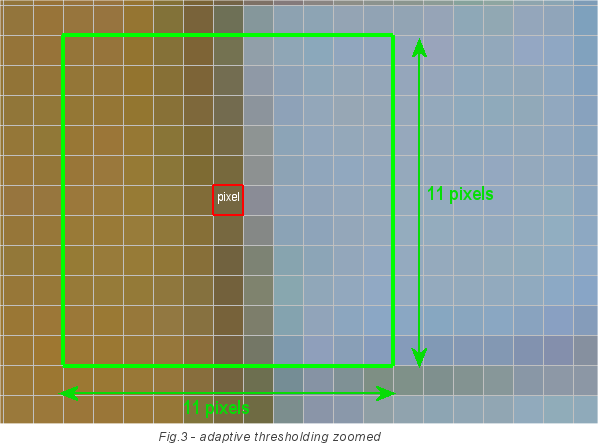
To correctly convert images to monochrome, we will use an adaptive selection of the threshold. It does not use a fixed threshold value of 128. Instead, it counts the threshold for each pixel separately. It takes a square with a side of 11 pixels and with the center in our pixel and summarizes the intensity of all points. The average intensity value will be the threshold for a given pixel. The intensity formula for the current pixel: threshold = sum / 121, where 121 = 11x11. If the intensity of our pixel is above the threshold value, then it is converted to white, if not, then to black. In the image below, the pixel for which the threshold is determined is marked in red. And these calculations are made for each pixel. Therefore, this step is so slow, because the algorithm requires a width * height * 121 readings of the image pixel.

Integer form

This step can be optimized using the “Integer form”. The integer form is an array of integers with image dimensions. The meaning is ingenious and simple. Take an image. Suppose we have a 12x12 area, where the pixel intensity is 1 (in the real world it does not happen, because it is never that simple), the integer image is the sum of all pixels from the top left to the current (bottom right).



The following image demonstrates how an integer image can be useful. The goal is to calculate the sum of pixels in a gray rectangle.
Formula: Amount = DC-B + A. In our case: 110-44-40 + 16 = 42 (try to count manually).
Instead of reading all the pixels from the gray rectangle (which can be much larger than in the example), we only need one memory read. This is a significant algorithm optimization. But even with it, converting an image into monochrome is very hard.

How to determine the angle of rotation

Webcam is not a scanner. And the picture will never be perfectly smooth, which means in the order of things a bit beveled and rotated image. To determine the angle of rotation, we will use the fact that an image with a sudoku always has horizontal and vertical lines. We will identify the most expressive and bold lines near the center of the image. The most expressive lines are not subject to noise. The algorithm for finding monochrome lines in an image is called the Hough transform.

How it works? You should remember the school formula y = (x * cos (theta) + rho) / sin (theta).


Where theta is the angle of the line, and rho is the distance from the line to the center of coordinates (0, 0).
It is important that the line can be described by only two variables: the angle of inclination and the distance to the center of coordinates.

The algorithm passes through all the pixels in a monochrome image, skipping white pixels. When he hit the black pixel, he tries to “draw” all sorts of lines passing through this pixel in 1 degree increments. This means that each pixel has 180 imaginary lines passing through it. Why not 360? Yes, because the angles of 180-360 are copies of lines with angles of 0-180 degrees.

This set of imaginary lines is called the accumulator, a two-dimensional array with theta and rho dimensions, which were in the formula above. Each imaginary line is represented by one value in the accumulator. By the way, the method is called conversion, because it converts lines from (x, y) into an array (theta, tho). Each imaginary line adds value to the drive, increasing the likelihood that the imaginary line coincides with the real one. It is like a vote. Real lines have the most “votes”.

After all the pixels and their 180 imaginary lines have "voted", we need to find the maximum value in the drive. (By the way, it is called accumulator because it accumulates votes) The winner of the vote is the most expressive line. Its theta and rho parameters can be used with the formula above to draw it.

The following image shows a small example. On the left we have a line consisting of three pixels. You know for sure that this is a diagonal line from left to right, but for a computer it is not so obvious.



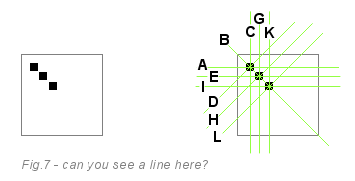
Looking at this image, you can understand how line detection works. The Hough transform algorithm skips white pixels. On each black pixel, he draws four imaginary green lines (actually 180, but for simplicity we take four) passing through the current pixel. The first pixel votes for lines A, B, C and D. The second pixel votes for lines E, B, G, H. The third for I, B, K, L. All three pixels voted for line B, and the remaining lines received only one voice. Thus, line B won the vote.

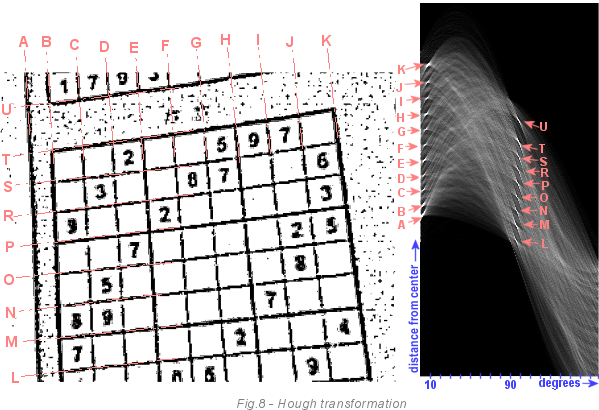
The following image is a more complex example. On the left, we see the sudoku grid, and on the right, the drive array after passing through the Hough transform algorithm. Bright, bright areas are lines that have received many votes. Darkness means that we do not have a chance to find a line with such parameters in the image. Concentrate only on bright points. Each line (AU) has a bright point in the drive. You can see that all the lines are slightly rotated (about 6 degrees). Line A is less turned than line K. Because the image is not only turned, but also skewed. Also, if you look closer, you will see that lines A and B are closer to each other than B and C. This can be seen in both images.



Converting Hough is important to understand if you want to engage in pattern recognition. The concept of virtual lines, which can be real using a vote, can be extended to any geometric shape. The line is the simplest of them, so it is the easiest to understand.

If you need to find a circle, then you need a drive with three dimensions: x, y and r. Where x and y are the coordinates of the center of our circle, and r is the radius.
The Hough transform can be optimized by limiting the area and possible angles of the original image. We do not need to analyze all the lines, only those that are close to the center. In our case, it is from them that we can make a start.

How to define a grid

To get numbers from the sudoku grid, we need to determine where our grid starts and ends. This part is the simplest part for the human brain, but the most complex for the computer. Why? Why not use the lines found using the Hough transform in the previous step? They have too much extra data. Very often, newspapers and magazines print several sudoku side by side (hmm, they obviously do not count on computer recognition of the latter). The image will have too many extra lines. For example, look at the image below:



It is very difficult for a computer to determine which lines belong to what we need, and which lines are just information noise. Where is the end of our grid and the beginning of the next.
To solve this problem, we will not define black lines. Instead, we will define white areas around the grid. In the next image, you can see this. Green line 1 never intersects with black pixels while line 2 does it 10 times. This means that behind the grid there is a line 1 rather than a line 2. Just by counting how many times the green line crosses black pixels, we can conclude that it is outside the grid. Simply calculate how many transitions from white to black pixel under the line. By the way, you do not need to go over each line, it is enough to perform these actions every third line to increase the speed of execution.



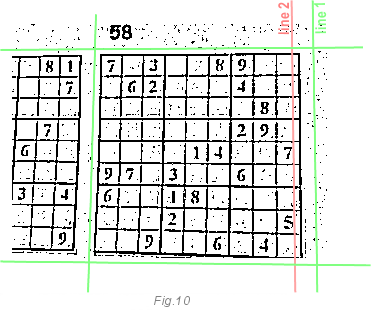
After we have defined the boundaries, run the Hough transform algorithm to accurately determine the grid lines. Until now, we have not taken care of the distortions and other defects of the image. Only about the angle of rotation. This step will fix this. By running the Hough transform, we get the exact positions of the grid lines. This will help determine the numbers in the grid.

TODO : This step may be more resistant to noise. In the next version, I plan to combine the current method with Haar-like algorithms to determine the grid angles. I hope this will increase the quality. The problem may be that the method with Haar-like algorithms works well with solid regions, and not with lines. The lines occupy a small area, so the difference between the light and dark rectangle is not so great.
I wonder what happens when I try to detect a 10x10 grid ...

How does OCR work

Once we have determined where the numbers should be, we need to recognize them. It is relatively easy. The alphabet only numbers from 1 to 9.

Theory

Each recognition algorithm has three steps:

• Determination of required signs
• Training
• Classification (recognition in runtime)

Identifying required attributes is part of application development. For example, the number one is thin and high. This is what distinguishes it from the rest. The number 8 has two circles, in the upper half and in the bottom, and so on.
Determining the necessary attributes can be difficult and non-intuitive work, depending on what needs to be recognized. For example, what is needed to recognize someone's face? Not any, but any particular.

Zones

In our application, we used the method of density zones. The next step (this must be done in advance) is to train the application on numbers from 1 to 9. You can find these images in the ./res directory. They are reduced to size 5x5, normalized and stored in the static array OCRDigit :: m_zon [10] [5] [5], which looks like this:

Reducing to size 5x5 is called zoning or zoning. The array above is called the density function.
Normalization means that the density varies from 0 to 1024. Without zone normalization, it is impossible to compare correctly.
What happens during program execution: when a digit is obtained from the original image, it is reduced to a size of 5x5. After that, each of its pixels is compared with each pixel of nine digits from the trained array. The goal is to find a digit with minimal difference.

This method is invariant to the image size, since in any case we use 5x5 zones. He is sensitive to turns, but we have already taken care of this before. The problem is that it is sensitive to position and displacement, and also does not work with negatives (white on black) and numbers upside down.

Width / Height ratio

The number one is a special case. Since it is similar to 4 and 7, the definition method given above may be unreliable. The specific parameter of the unit: in our case, its width is 40% smaller than the height. There is no other such digit with the same ratio. We already have 25 zones (signs), so this is the 26th sign.

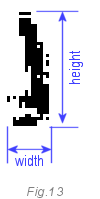
TODO : In the next version, the quality of OCR can be improved by introducing new features. For example, the numbers 5.6 and 9 are very similar when using zoning. In order to distinguish them, we can use their profiles as attributes. A feature of the feature is the number of pixels (distance) between the edge of the frame of the digit and its border.
In the image below, you can see that the profiles of numbers 5 and 6 are similar, but they differ from profile 9. The left profile 5 and 9 are similar, but different from profile 6.



You can add a few more improvements. Professional OCR engines use many features. Some of them are very exotic.

Adjusting OCR Results

Once the OCR is completed, the results are adjusted according to the sudoku rules. In the same row, column and 3x3 block can not be the same digit. If the rule is violated, it is necessary to introduce adjustments in the results obtained. We will replace the wrong number with that of the remaining ones. For example, in image 12 above, the result is 5 because diff = 5210, which is the smallest difference value. The next possible result is 6, since diff = 5508 in this case. Thus, we will replace 5 by 6. In order to decide which of the two digits is incorrect, we will compare the values ​​of their differences with their samples, and one with a lower value will be considered correct. The source code of the correction can be found in the function SudSolver :: Fixit ();

How the Sudoku Solver Function Works

There are several ways to solve sudoku. We use three simple methods that work together and complement each other: open numbers, hidden numbers and brute force.

Bust

It is the most widely used method by programmers, which accurately gives a solution regardless of the level of complexity. But the search can be very long, it depends on the depth of the recursion. You will never know how many iterations you need. During the search, the cells are alternately possible from values ​​from 1 to 9 and the solution to the sudoku with the set number continues. If we are at a dead end (we got the same numbers in one line / column / block, then we change the number to the next). In fact, there may be more than one solution, but it will be cool if we find at least one. (The translator had a bust in the solution and it worked surprisingly quickly).

First, it is necessary to prepare a table of candidates — possible values ​​for each empty cell. The image below explains exactly what the candidates are. They are painted blue. According to the rules of Sudoku, the first cell can contain only the numbers 1, 4, 8. The triple cannot be there, since it is already two cells below.



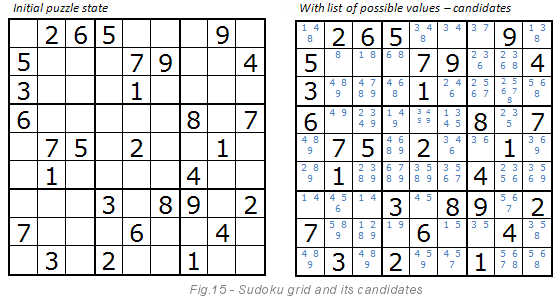
The iteration method tries to combine all the blue numbers until it finds a solution. Let's look at the first cell. The algorithm begins with one, in the fifth cell there will be a value of 3, and so on. If a digit does not agree with other values, then the algorithm tries another one. For example, the sixth cell on the left also has the number 3 as a candidate, but this is inconsistent with the fifth cell, so the algorithm will try the next digit, that is, 4, etc.
Busting can be very slow if the solution requires a lot of iteration. For example, the following image is a very bad case for our algorithm. Starting from the top left cell, there will be too many searches, but there is some good news: start with the cell, where there are fewer options. This will speed up the decision.



There are a few more optimizations to increase the performance of the algorithm, such as sorting the recursive sequence from the cells with the fewest candidates for the cells with the most. But we do not use this algorithm, since it is only a partial optimization. All sudoku have bad cells and are not processed so quickly for real-time applications.

Open numbers

The image below explains this method. If a cell has a single candidate, then we can confidently say that it is this number that should stand in this cell. After setting the value, the next step is to rebuild the list of candidates. The list of candidates is reduced while there are single candidates. This is an obvious and simple method for computers. But not as obvious to people as it seems to me. Live players can not keep a list of candidates in the head and constantly rebuild it and adjust.

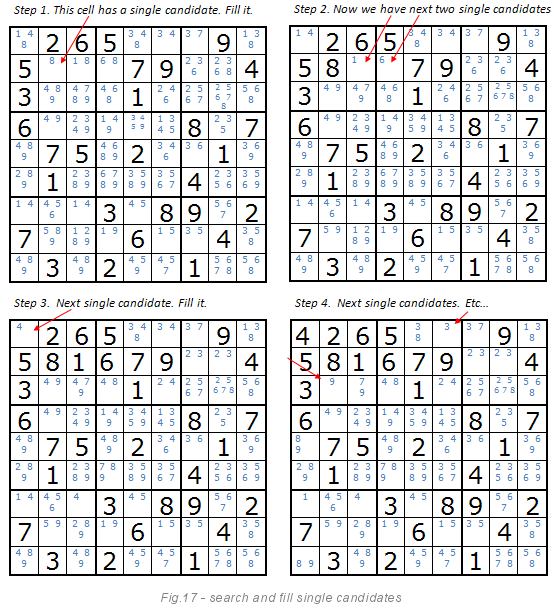
Hidden numbers

As before, the image below explains this method. Look at the number 7. If you solve a sudoku, you will most likely say that the seven must be in the specified cell.



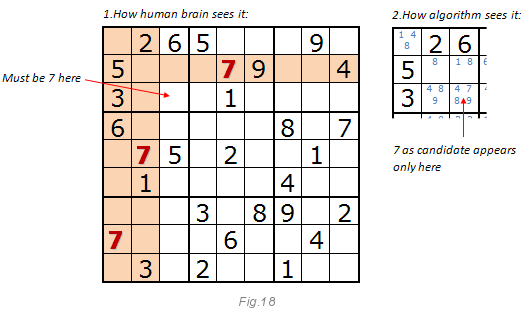
Even if this cell has four candidates: 4, 7, 8, 9 (see Fig. 15), the trick is that we are looking for unique numbers from candidates in a 3x3 block, in a row and in a column. The method may be able to solve the entire puzzle entirely, but it works better with method 2. When the single candidates run out of the open numbers method, the hidden numbers method enters the scene.

Combining all methods together

For at important speed processing and solutions. Brute force is not too fast. Thus, we will use a combination of all three methods. Methods 2 and 3 are very fast, but only fast puzzles can solve. Since we ask the application to solve the puzzle for us, this means that it is really difficult. Below is the algorithm of work. On the left side are the fast methods 2 and 3. And only if they cannot solve the puzzle, does the control go to the right side with the brute force method, reducing the work for this algorithm.



Only if methods 2 and 3 cannot solve the puzzle, does the program begin to override the values. And even then, the iteration algorithm is time limited to 600,000 iterations. There are also three attempts, after which the program gives up. Between each attempt, the recursive sequence is rearranged randomly with the hope that the new sequence will help solve the puzzle faster. If we couldn’t solve the sudoku, we might be lucky with the next frame of the camera. The presented block diagram is described in the function SudSolver :: SolveMe ().

Solution Buffering

When the solution is found, we store it in an array of type SudResultVoter. Buffering is necessary because OCR does not guarantee 100% correctness of the result, and we get different solutions from time to time. To avoid an unstable solution, we will always show the strongest (for the accuracy of the last 12 solutions). From time to time the array is reset, forgetting old decisions and giving a chance to new ones.

Video

TODO:

Some ideas for the future:

• Rewrite the program for Android. I wonder how it will work on smartphones
• To parallelize some functions on multiprocessor systems. Today, most PCs have at least two cores. Typically, parallelization gives a performance boost. But with the solution through the webcam, we need not so much speed as accuracy and quality. In theory, task parallelization should improve operations on similar frames, but with different settings. After all the tasks are completed, we just take the best result.

Download demo - 170 KB
Download sources - 307 KB

Also there is a mirror of source codes on GitHub: github.com/NeonMercury/Realtime-Webcam-Sudoku-Solver