Monads in terms of category theory
Introduction
It seems that the monads in programming have become a mystery of the century. And for this there are two reasons:- insufficient knowledge of category theory;
- many authors try not to mention the category at all.
We will start with a simple introduction to categories and functors, then we will define monads, give simple examples of monads in categories and at the end give monadic terminology used in programming languages.
I am sure that monads are almost elementary in terms of categories.
')
Content
Category
A category consists of objects and morphisms between them. The term “morphism” is not entirely correct (it is not obliged to transform something), therefore, the morphism is often called an “arrow” in order to show its abstract essence.We will use the term “arrow” in all cases, except when the arrow denotes a certain function, then we will call it “morphism”, but for me it will still remain an arrow.
It doesn’t matter what an object or an arrow is, it’s only important to fulfill the following properties:
The arrow is drawn between the objects (the object may be the same); This is denoted as follows: f: a → b , where f is an arrow, and a and b are objects.
- For arrows f: a → b and g: b → c, there is an arrow h: a → c called composition : h = g ° f .

- For each object a, there is a single arrow , id a : a → a , such that for any f: a → b the following is true:
f ° id a = f and for any g: c → a we have id a ° g = g . - The composition is associative: f ° (g ° h) = (f ° g) ° h .
Remark In view of the extremely abstract nature of this record, we cannot expect that “all objects” or “all arrows from a to b” form a multitude. Categories where they are sets are called "small" or "locally small."
Category examples
Examples of "classic" categories:- Set - the category of all sets. Its objects are all sets, and morphisms are functions over sets.
- Setf is the category of all finite sets and functions between them.
- Rel is a category where objects are all sets, and binary relations play the role of morphisms. The composition is combined through the internal union.
- Part is the category of all sets and partial functions as morphisms. A partial function from X to Y is a function from the subset X o ⊂ X to Y :
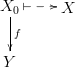
- Top is the category of all topological spaces and continuous functions between them.
- Any group can be considered as a category: a group of elements is a morphism over a single object.
The identity function is the neutral element of the group. A composition is multiplication. - A partially ordered set can be represented as a category. The elements of a set are objects. Add one arrow a → b for each pair a, b so that a <b and a single arrow a → a for each a .
For each pair of objects, there is no more than one arrow and, since the partial order is transitive, we have a composition ( a <b, b <c => a <c ), that is, you can not worry about its associativity. - As a special case of the last example, the set of integers [N ... M] can be considered a category.
- Any directed graph can be transformed into a category, if we consider its paths as arrows. The empty path is a single morphism, and the concatenation of paths will be a composition.
- Natural numbers as objects, matrices as arrows. Any NxM matrix is an arrow N → M. Multiplication of matrices will play the role of composition, and the unit matrix NxN will be the unit arrow N → N.
Additional material
It is easy to define isomorphism in a category — it is the one that has an inversion. That is, if we have f: a → b and g: b → a , and we have f ° g = id b and g ° f = id a . We will need this definition later. It is also possible to define monomorphism and epimorphism, it is somewhat more complicated and is beyond the scope of this article.Remember the objects [0 ... N] from the last chapter? There are special categories: 1 = [0] and 2 = [0 ... 1] . The first is one object with a single morphism, the second is two objects and three morphisms.
Do the categories themselves form a category? Yes, but then we should define the arrows between them. They are second-order arrows and are called functors.
Functor
The functor maps one category to another. In order to do this, we need to map objects from the first category to the second and arrows (morphisms) from the first category to arrows in the second category in a consistent way.What consistency are we expecting? Let X and Y be two categories; we define the functor F: X → Y. Now we need to map objects from X to Y , having for each a in X an object F (a) in Y and for each arrow f in X we should have an arrow F (f) in Y.
For consistency, the following rules should be followed:
- for f: a → b we have F (f): F (a) → F (b) - the domain and code domain are saved;
- for id a : a → a, we have F (id a ) = id F (a) : F (a) → F (a) - one is preserved;
- for f: a → b and g: b → c F (g ° f) = F (g) ° F (f) - the composition is preserved.
Examples of functors
- The identity functor for the category X. Although the identity of X → X keeps objects and arrows unchanged, it is still a functor.
- Setf Set is a functor that includes Setf in a Set , mapping finite sets to themselves, the same with functions. Note that this is not an identical functor.
- Set → Top is similar to the previous example; this functor makes Set a part of Top . Each set is mapped to a discrete topological space.
- For any set A, we can define the following functor:
(- xA): Set → Set - it will display any set X in the Cartesian product X × A. - For any set A, you can define the functor P A : Set → Set , which maps any set X to X A - a set of functions from A to X.
- Set Part introduces sets in partial functions - displays the sets and functions in them.
- The inverse of Clause 6 is the + Null functor : Part → Set — this functor adds a “ Null extension” to each set X ↦ (X + Null) so that the partial function X → Y is mapped to the function (X + Null) → (Y + Null) .
Exercise . Define the same extension for partial functions.
Let's look at small categories and their functors.
- If we take groups as categories, then what are their functors? The functor must preserve a single morphism and composition. Therefore, the functor is a group homomorphism.
- Any function that preserves the order (the so-called monotone) between two partially ordered sets is a functor.
- Take a pair of directed graphs and a mapping that preserves the edges. We can extend this mapping to a function that maps the path from one graph to a path on another graph. This function, by definition, saves links and empty paths, so this is a functor from one category created by a graph to another.
- Remember category 1 ? And so, what would a functor from 1 look like in a category C ? 1 has only one object and the same morphism. Thus, the definition of this functor is equivalent to choosing an object from C and vice versa — for any object X in category C we can define the functor Point X : 1 → C.
Natural transformation
It must be the hardest part. Suppose that we have two functors F, G: X → Y. The natural transformation η: F → G is defined when for each object x ∈ X there is an arrow η (x): F (x) → G (x) in Y and we have the following property:- for all f: a → b, the following equality holds: G (f) ° η (a) = η (b) ° F (f) .
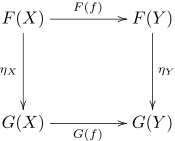
Therefore, it is called “natural” - it acts consistently with the actions of functors on arrows.
Examples of natural transformations
- Remember the point functor? And so, if in category C we have an arrow f: a → b , this arrow defines a natural transformation from Point a to Point b . This is a one-to-one relationship between the transformation of the point functor and the category arrows.
- Take two sets A and B and the function f: A → B. This function defines a natural transformation between the functors (- xA), (- xB): Set → Set . (- xf): (- xA) → (- xB) by the following formula: (x, a) (x, f (a)) .
You can write this definition in the following form:(define (cartesian f) (lambda (x a) (list x (f a))))
, :
(define (return x) (lambda (a) (x)))
C T: C → C : η: 1 → T μ: T ° T → T. T(η): T → T ° T , T η T(μ): (T ° T) ° T → T ° T.
:
- T(η) ° μ T → T
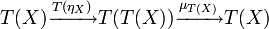
- T(μ) ° μ μ ° μ:
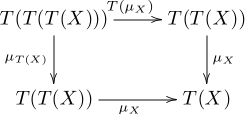
- C , .
- , G. MG Set. :
X ↦ X × G.
u(X): X → X × G x (x, e), e .
MG(MG(X)) = (idX, mG), mG . - Set. , List, X (x1, x2, x3...) X, . , u m. uX: X → List(X) x ∊ X mX: List(List(X)) → List(X) .
. , «computer science».
, - , , ?
( ) C: X → X , ∀ x ∊ X x <= C(x) C(C(x)) = C(x).
, , - , , - . - .
Part. A :
PlusNull: X ↦ (X+Null)
, Part Set. Set Part, .
? uX: X → (X+Null) mX: ((X+Null)+Null) → (X+Null).
, Null Null. Lisp :
(define (ux x) x)
(define (mx x) x)
Set. A :
X ↦ (X × A)A
A , , (X × A)A X X, A → (A × X), , X.
? uX: X → (A × X)A x ∊ X , A x X.
Lisp:
(define (ux x)
(lambda (a) (list a x)))
mX: (A × (A × X)A)A → (A × X)A?
mX: (A × (A × X)A)A, A , ( A , X ). , , A?
Lisp:
(define (mx f)
(let (tr1 out1)
((car f) (cadr f))) ; f: A → (A × (A × X))^A
(lambda (a)
(let a1 (tr1 a)) ;
(let f2 (out1 a)) ;
(let (tr2 out2) ((car f2) (cadr f2))) ;
(list (tr2 a1) (out2 a1))))
. , .
, f: X → Y, X «», Y «».
, ; , 100% , . , « » .
, , .
NullObject NaN.
, X, (Y+Null), .
, , .
IO Haskell
Haskell IO, , .. , . , A , , X .
. A String, «», «».
, , getc, , , putc, .
, .
- .
- , , .
- “Comprehending Monads” Frederik Eaton — .
- Haskell u return, m join
- Haskell List .
- map/reduce Google.
Source: https://habr.com/ru/post/125782/
All Articles