Search for a path on a hexagonal grid
In fact, I will not reveal anything new to anyone, but what I found was with cunning mathematics (or rather, not so cunning, but still difficult for me personally to comprehend), and then my bike turned out to be simple.
And so we already have:
Search on a regular rectangular grid.
What we need:
Search the hexagonal grid with minimal effort.
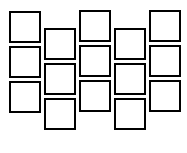
The first idea is simply to shift everything through the column:
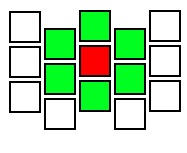
Then the neighbors of the current cell look like this:
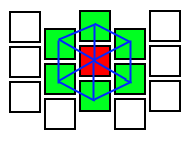
As you can see, the connections between the cells in theory should form just a hex:
But immediately suspicions creep in that there should be no squares at all, but rectangles:
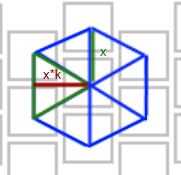
How not difficult to calculate the k in the figure will be equal to sqrt (3) / 2
As a result, we get a grid
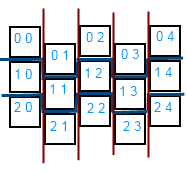
Where the size of each cell is w = sqrt (3) / 2, h = 1, with each odd column (if starting from 0) shifted by 0.5
Then everything goes easier to translate the coordinates in the cell number, adjusted for even / odd column:
To the contrary, a cell of the field is transferred to the coordinates:
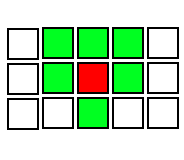
Now we need to get all the neighbors of the selected cell.
They will look something like this for even columns (and symmetrically for odd columns).
')
Now, for a full-fledged implementation, there’s just a lack of a way to find the distance between two cells, you can of course use the trite Euclidean, but this is not our option. We take the diagonal distance on a regular grid as the base:
Our situation is similar (there are also diagonal moves), only to shift vertically (considering the orientation of the grid as in the example), you can either take one vertical step, or 2 horizontally.
But there is a small detail here, if the distance is measured between two cells from different columns, then there will still be an unrecorded displacement in the cell floor. Therefore, yd should be defined a little differently:
It now remains to incite A * to this all, for example, as I did here , and tadam:
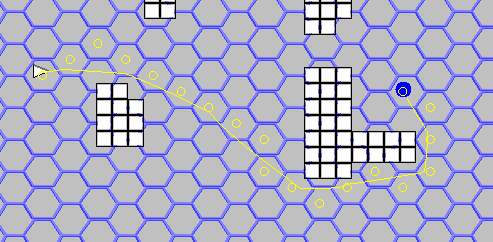
Of course, there are more beautiful mathematical ways of manipulating the hexagonal grid, but in my opinion this method turned out to be simple enough to have the right to life (and plus in the performance test it showed quite good results).
And so we already have:
Search on a regular rectangular grid.
What we need:
Search the hexagonal grid with minimal effort.
General grid structure
The first idea is simply to shift everything through the column:

Then the neighbors of the current cell look like this:

As you can see, the connections between the cells in theory should form just a hex:

But immediately suspicions creep in that there should be no squares at all, but rectangles:

How not difficult to calculate the k in the figure will be equal to sqrt (3) / 2
As a result, we get a grid

Where the size of each cell is w = sqrt (3) / 2, h = 1, with each odd column (if starting from 0) shifted by 0.5
Coordinate transformation
Then everything goes easier to translate the coordinates in the cell number, adjusted for even / odd column:
(x,y)=>(x/w, (y-(x/w)%2)/h)To the contrary, a cell of the field is transferred to the coordinates:
(i,k)=>(i*w, k*h+h/2*(i%2))Neighbors
Now we need to get all the neighbors of the selected cell.
They will look something like this for even columns (and symmetrically for odd columns).

')
(i,k)=>(
(i+1,k),
(i-1,k),
(i,k+1),
(I,k-1),
(i+1,k+(1-2*i%2)),
(i-1,k+(1-2*i%2)))
Distance between two cells
Now, for a full-fledged implementation, there’s just a lack of a way to find the distance between two cells, you can of course use the trite Euclidean, but this is not our option. We take the diagonal distance on a regular grid as the base:
xd = abs(p1.X - p2.X);
yd = abs(p1.Y - p2.Y);
diagonal = min(xd, yd);
straight = xd + yd;
result = sqrt(2) * diagonal + (straight - (2 * diagonal)));
Our situation is similar (there are also diagonal moves), only to shift vertically (considering the orientation of the grid as in the example), you can either take one vertical step, or 2 horizontally.
//
if (xd >= yd * 2)
{
result = xd;
}
//
else
{
result = xd + (yd – xd/2);
}
But there is a small detail here, if the distance is measured between two cells from different columns, then there will still be an unrecorded displacement in the cell floor. Therefore, yd should be defined a little differently:
yd =abs((p1.Y + (p1.X%2)/2) – (p2.Y + (p2.X%2)/2));It now remains to incite A * to this all, for example, as I did here , and tadam:

Instead of epilogue
Of course, there are more beautiful mathematical ways of manipulating the hexagonal grid, but in my opinion this method turned out to be simple enough to have the right to life (and plus in the performance test it showed quite good results).
Source: https://habr.com/ru/post/125751/
All Articles