Algorithm for Finding N First Primes - Atkin Sieve
In the process of implementing one program, I was faced with the task of finding primes up to a number N of order  . On Habré, they have repeatedly written about various methods and methods, but did not mention the main method of solving, which I will try to correct today.
. On Habré, they have repeatedly written about various methods and methods, but did not mention the main method of solving, which I will try to correct today.
The algorithm has asymptotic complexity. and requires
and requires  bit of memory. On input order values
bit of memory. On input order values  Atkin's sieve is faster than the sieve of Erastofen by 9.2 times. I will give a graph of the growth of the superiority of the algorithm Atkin on the numbers from 2 to
Atkin's sieve is faster than the sieve of Erastofen by 9.2 times. I will give a graph of the growth of the superiority of the algorithm Atkin on the numbers from 2 to  :
:
')
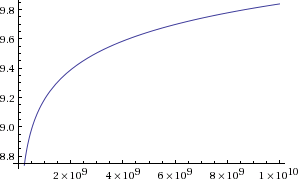
As a result, the following execution speed can be observed:
For convenience and brevity, we will create an abstract class from which we will inherit Atkin sieve implementations. In the future we will only create different variants of the class.
Create a basic implementation of the algorithm:
The execution time of the basic (classical) version of the algorithm:
Recall that in the C # language, operations with the ulong type take about 3 times longer than with the int type. In the program, when calculating large numbers, the values still pass for int.MaxValue, so we find an empirical level of use. Here it is equal to 858599509. Insert the condition and get the final acceleration:
That's all. Thank you for your attention - I tried not to be very dry.
 . On Habré, they have repeatedly written about various methods and methods, but did not mention the main method of solving, which I will try to correct today.
. On Habré, they have repeatedly written about various methods and methods, but did not mention the main method of solving, which I will try to correct today.The algorithm has asymptotic complexity.
 and requires
and requires  bit of memory. On input order values
bit of memory. On input order values  Atkin's sieve is faster than the sieve of Erastofen by 9.2 times. I will give a graph of the growth of the superiority of the algorithm Atkin on the numbers from 2 to
Atkin's sieve is faster than the sieve of Erastofen by 9.2 times. I will give a graph of the growth of the superiority of the algorithm Atkin on the numbers from 2 to  :
:')

As a result, the following execution speed can be observed:
| 10,000,000 | 0.15 seconds |
| 100,000,000 | 2.16 seconds |
| 1,000,000,000 | 48.76 seconds |
For convenience and brevity, we will create an abstract class from which we will inherit Atkin sieve implementations. In the future we will only create different variants of the class.
public abstract class AAtkin
{
internal readonly int _limit;
public bool [] IsPrimes;
protected AAtkin( int limit)
{
_limit = limit;
FindPrimes();
}
public abstract void FindPrimes();
}
Create a basic implementation of the algorithm:
public override void FindPrimes()
{
IsPrimes = new bool [_limit + 1];
double sqrt = Math .Sqrt(_limit);
var limit = ( ulong ) _limit;
for ( ulong x = 1; x <= sqrt; x++)
for ( ulong y = 1; y <= sqrt; y++)
{
ulong x2 = x*x;
ulong y2 = y*y;
ulong n = 4*x2 + y2;
if (n <= limit && (n%12 == 1 || n%12 == 5))
IsPrimes[n] ^= true ;
n -= x2;
if (n <= limit && n%12 == 7)
IsPrimes[n] ^= true ;
n -= 2 * y2;
if (x > y && n <= limit && n%12 == 11)
IsPrimes[n] ^= true ;
}
for ( ulong n = 5; n <= sqrt; n += 2)
if (IsPrimes[n])
{
ulong s = n*n;
for ( ulong k = s; k <= limit; k += s)
IsPrimes[k] = false ;
}
IsPrimes[2] = true ;
IsPrimes[3] = true ;
}
The execution time of the basic (classical) version of the algorithm:
| 1,000,000 | 0.03 seconds |
| 10,000,000 | 0.39 sec |
| 100,000,000 | 4.6 seconds |
| 1,000,000,000 | 48.92 seconds |
Recall that in the C # language, operations with the ulong type take about 3 times longer than with the int type. In the program, when calculating large numbers, the values still pass for int.MaxValue, so we find an empirical level of use. Here it is equal to 858599509. Insert the condition and get the final acceleration:
IsPrimes = new bool [_limit + 1];
double sqrt = Math .Sqrt(_limit);
if (sqrt < 29301)
{
for ( int x = 1; x <= sqrt; x++)
for ( int y = 1; y <= sqrt; y++)
{
int x2 = x * x;
int y2 = y * y;
int n = 4 * x2 + y2;
if (n <= _limit && (n % 12 == 1 || n % 12 == 5))
IsPrimes[n] ^= true ;
n -= x2;
if (n <= _limit && n % 12 == 7)
IsPrimes[n] ^= true ;
n -= 2 * y2;
if (x > y && n <= _limit && n % 12 == 11)
IsPrimes[n] ^= true ;
}
for ( int n = 5; n <= sqrt; n += 2)
if (IsPrimes[n])
{
int s = n * n;
for ( int k = s; k <= _limit; k += s)
IsPrimes[k] = false ;
}
}
else
{
var limit = ( ulong ) _limit;
for ( ulong x = 1; x <= sqrt; x++)
for ( ulong y = 1; y <= sqrt; y++)
{
ulong x2 = x*x;
ulong y2 = y*y;
ulong n = 4*x2 + y2;
if (n <= limit && (n%12 == 1 || n%12 == 5))
IsPrimes[n] ^= true ;
n -= x2;
if (n <= limit && n%12 == 7)
IsPrimes[n] ^= true ;
n -= 2 * y2;
if (x > y && n <= limit && n%12 == 11)
IsPrimes[n] ^= true ;
}
for ( ulong n = 5; n <= sqrt; n += 2)
if (IsPrimes[n])
{
ulong s = n*n;
for ( ulong k = s; k <= limit; k += s)
IsPrimes[k] = false ;
}
}
IsPrimes[2] = true ;
IsPrimes[3] = true ;
}
That's all. Thank you for your attention - I tried not to be very dry.
Source: https://habr.com/ru/post/125620/
All Articles